Навигация
Пример
2.1.2 Пример
Пусть ![]() – натуральное число. Обозначим через
– натуральное число. Обозначим через ![]() – совокупность всех непустых подмножеств множества
– совокупность всех непустых подмножеств множества ![]() . Два таких подмножества объявим толерантными, если у них есть хотя бы один общий элемент. Законность такого определения очевидна: рефлексивность и симметричность отношения легко проверяются.
. Два таких подмножества объявим толерантными, если у них есть хотя бы один общий элемент. Законность такого определения очевидна: рефлексивность и симметричность отношения легко проверяются.
Множество ![]() называется
называется ![]() -мерным симплексом. Это понятие обобщает понятия отрезка, треугольника и тетраэдра на многомерный случай. Числа
-мерным симплексом. Это понятие обобщает понятия отрезка, треугольника и тетраэдра на многомерный случай. Числа ![]() интерпретируются как вершины симплекса. Двухэлементные подмножества – как ребра, трехэлементные как плоские грани,
интерпретируются как вершины симплекса. Двухэлементные подмножества – как ребра, трехэлементные как плоские грани, ![]() -элементные подмножества – как
-элементные подмножества – как ![]() -мерные грани. Толерантность граней симплекса
-мерные грани. Толерантность граней симплекса ![]() означает их геометрическую инцидентность – наличие общих вершин. Число всех элементов из
означает их геометрическую инцидентность – наличие общих вершин. Число всех элементов из ![]() равно
равно ![]() .
.
Множество ![]() с заданным на нем отношением толерантности
с заданным на нем отношением толерантности ![]() называется пространством толерантности. Таким образом, пространство толерантности есть пара
называется пространством толерантности. Таким образом, пространство толерантности есть пара ![]() .
.
2.1.3 Пример
Пусть ![]() – произвольное множество. Обозначим через
– произвольное множество. Обозначим через ![]() совокупность всех непустых подмножеств множества
совокупность всех непустых подмножеств множества ![]() . Толерантность
. Толерантность ![]() на
на ![]() задается условием:
задается условием: ![]() , если
, если ![]() .
.
Пространство ![]() играет роль "универсального" пространства толерантности.
играет роль "универсального" пространства толерантности.
2.1.4 Пример
Возьмем произвольное множество ![]() (для наглядности можно представить отрезок на прямой). Пространство толерантности
(для наглядности можно представить отрезок на прямой). Пространство толерантности ![]() состоит из всех числовых функций, определенных на этом множестве, т.е. функций, которые каждому элементу из
состоит из всех числовых функций, определенных на этом множестве, т.е. функций, которые каждому элементу из ![]() сопоставляют некоторое число. Две функции будут толерантными, если хотя бы на одном элементе из
сопоставляют некоторое число. Две функции будут толерантными, если хотя бы на одном элементе из ![]() эти функции принимают одно и тоже значение (если, другими словами, графики этих функций пересекаются).
эти функции принимают одно и тоже значение (если, другими словами, графики этих функций пересекаются).
Существует еще один способ задания отношений толерантности. Рассмотрим соответствие ![]() . Множество всех образов элемента
. Множество всех образов элемента ![]() при соответствии
при соответствии ![]() мы обозначим
мы обозначим ![]() . Отношение
. Отношение ![]() на множестве
на множестве ![]() задается условием:
задается условием: ![]() , если у элементов
, если у элементов ![]() и
и ![]() существует образ, т.е. если
существует образ, т.е. если ![]() .
.
Установим основные свойства отношения ![]() :
:
Отношение ![]() всегда симметрично.
всегда симметрично.
Это следует из того, что ![]() .
.
Отношение ![]() рефлексивно тогда и только тогда, когда соответствие
рефлексивно тогда и только тогда, когда соответствие ![]() определено на всем
определено на всем ![]() .
.
В самом деле, в этом и только в этом случае множество ![]() .
.
Если на элементе ![]() отношение
отношение ![]() не рефлексивно (не выполняется
не рефлексивно (не выполняется ![]() или
или ![]() ), то соотношение
), то соотношение ![]() не выполнено ни для какого
не выполнено ни для какого ![]() , так как
, так как ![]() .
.
Если соответствие ![]() является функцией, т.е.
является функцией, т.е. ![]()
![]() состоит не более чем из одного элемента (в этом случае
состоит не более чем из одного элемента (в этом случае ![]() равносильно
равносильно ![]() ), то отношение
), то отношение ![]() транзитивно.
транзитивно.
Действительно, пусть ![]() и
и ![]() . Это значит, что
. Это значит, что ![]() и
и ![]() . Следовательно,
. Следовательно, ![]() , т.е.
, т.е. ![]() .
.
Из свойств следует, что всюду определенное соответствие ![]() определяет на
определяет на ![]() симметричное и рефлексивное отношение
симметричное и рефлексивное отношение ![]() , т.е. толерантность.
, т.е. толерантность.
Похожие работы
... чем «я», делает мировосприятие более многомерным, целостным, а значит более адекватным реальности [10, c.23-27]. Глава 2. Государственно-правовое регулирование проблем толерантности в современном обществе 2.1 Анализ правовых актов по проблемам толерантности В Декларации о ликвидации всех форм дискриминации на основе религии или убеждений, которая была принята Генеральной Ассамблеей ООН 25 ...
... сигналов, передающихся от одного живого организма другому (от родителей - потомкам) или от одних клеток, тканей, органов другим в процессе развития особи; 6. в математике, кибернетике – количественная мера устранения энтропии (неопределенности), мера организации системы; 7. в философии – свойство материальных объектов и процессов сохранять и порождать определенное состояние, которое в ...
... в отечественной теории и практике психологических измерений. Хотя концепт осмысленности измерения развивается с трансформацией идей Стивенса и разработкой проблем статистики и логики, его положения относительно шкалирования, по проблемам измерений в психологии и связанной с ними осмысленностью измерений требуют, на наш взгляд, критического анализа привычной практики использования психологического ...
... N(X)N, состоящее из тех и только из тех i, для которых = 1. Это объясняет, почему изложение вероятностных и статистических результатов, относящихся к анализу данных, являющихся объектами нечисловой природы перечисленных выше видов, велось [37, гл.4] на языке конечных случайных множеств. Множества как исходные данные появляются и в иных постановках. Из геологических реалий исходил Ж.Матерон ...

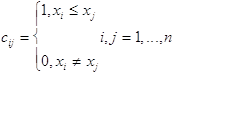
0 комментариев