Навигация
Щ (О, Р) базисная окружность, щ1 (О1, R1) – данная окружность, причем R1 ≠ R2;
64677
знаков
0
таблиц
57
изображений
1. щ (О, Р) базисная окружность, щ1 (О1, R1) – данная окружность, причем R1 ≠ R2;
2. О 
m – произвольная прямая;
3. А = m 
щ1, В = m щ2;
4. Точка Аґ - инверсна точке А, Вґ - Инверсна точке В;
5. щ1ґ (О, 
) – искомая окружность (рис 3).
Доказательство следует из анализа.
Рис 3
Исследование. Задача всегда имеет единственное решение.
Задача 4. Точка описывает хорду базисной окружности, отличную от диаметра. Построить линию, которую описывает инверсная точка.
Анализ. Пусть щ (О, Р) – базисная окружность инверсии, АВ – хорда, причем О 
АВ. Точка М описывает хорду АВ.
Заметим, что А = Аґ, В = Вґ. Прямая АВ не проходит через центр О, значит преобразуется в окружность щ1, которая проходит через центр.
Но так как дана не вся прямая, а только хорда АВ, то она преобразуется в дугу относительно окружности щ1 (концы дуг А и В), причем, во внешнюю дугу относительно окружности щ (О, Р), так как данная точка М расположена внутри окружности щ (О, Р).
Построение.
1. щ (О, Р), АВ – данная хорда;
2. щ1 – окружность, которая проходит через точки О, А, В;
3. 
АmВ – внешняя относительно щ, которая является искомой фигурой (рис. 4).
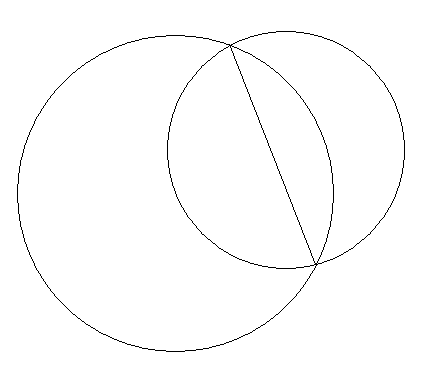
Рис 4
Доказательство следует из анализа.
Исследование. Задача всегда имеет единственное решение.
Задача 5. Найти такую точку, чтобы касательные, проведенные из нее к двум данным окружностям были равны ее расстоянию от данной точки.
Анализ. щ1 (О1, R1), щ2 (О2, R2) – данные окружности. Пусть точка А – искомая, тогда АК = АМ = АN. АК – касательная к щ1, АМ – касательная к щ2, то есть точка А а12 – радикальная ось окружности щ1 и щ2 и А а20 – радикальная ось щ2 и точки N, отсюда следует, что А = а12 
а20.
Построение.
1. щ1 (О1, R1), щ2 (О2, R2) – данные окружности, N – данная точка;
2. а12 – радикальная ось щ1 и щ2;
3. а20 – радикальная ось щ2 и N;
4. А = а12 а20, А – искомая точка (рис. 5).
Рис. 5
Доказательство. Точка А – радикальный центр щ1, щ2 и N.
Исследование.
1. Если щ1 и щ2 - концентрические, то задача не имеет решения.
2. Если N внутри щ1 (О1, R1) или щ2 (О2, R2), то решений нет.
3. Если радкальные оси параллельны, то решений нет.
4. Если радикальные оси совпадают, то задача имеет бесконечное множество решений.
Задача 6. Построить фигуру, инверсную сектору базисной окружности.
Анализ. Пусть щ (О, R) – данная базисная окружность, АmВО – данный сектор.
При инверсии точка А переходит в точку Аґ, часть луча ОА переходит во внешнюю его часть АґК∞. дуга АmВ при инверсии преобразуется в себя.
Точка В преобразуется в точку Вґ. ОВ преоюразуется в ВґL∞. Таким образом сектор базисной окружности АmВО преобразуется в фигуру, определяемую внешней частью луча, АґК∞, ВґL∞ и дугой АґmВґ.
Построение.
1. щ (О, R) – базисная окружность;
2. А ≡ Аґ, В ≡ Вґ;
3. ОА → АґК∞;
4. ОВ → ВL∞;
5. АmВ → АґmВґ;
6. К∞АґmВґL∞ - искомая фигура (рис. 6).
Доказательство. Доказательство следует из анализа и построения.
Исследование. Задача имеет всегда решение и притом единственное.
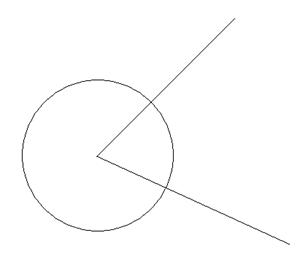
Рис. 6
Задача 7. Даны две окружности, касающиеся друг друга в точке А. приняв точку А за полюс инверсии построить фигуру, инверсную двум окружностям.
Анализ. Пусть щ1 (О1, R1), щ2 (О2, R2) – данные окружности, щ (А, R) - базисная окружность. В = щ щ2, С = щ щ2, D = щ щ1, К = щ щ1. при инверсии точки В, С, D и К преобразуются в себя, так как они принадлежат щ (А, R). Так как окружности щ1 и щ2 проходят через центр базисной окружности, то они преобразуются в прямые : l1 B, l1 C, l2 D, l2 К.
Построение.
1. щ1 (О1, R1), щ2 (О2, R2) – данные окружности, щ1 щ2 = А, щ (А, R) - базисная окружность;
2. В = В = щ щ2, В → Вґ;
С = С = щ щ2, С → Сґ;
3. D = щ щ1, D → Dґ;
К = К = щ щ1, К → Кґ;
4. l1 Вґ, l1 Сґ, l2 Dґ, l2 Кґ, l1 и l2 – искомые прямые (рис 7).
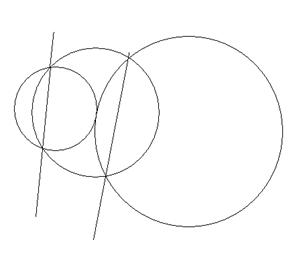
Рис. 7
Доказательство.Доказательство следует из анализа и построения.
Исследование. Задача имеет единственное решение.
Задача 8. через данную точку А провести окружность, ортоганальную двум данным окружностям.
Анализ. щ1 (О1, R1), щ2 (О2, R2) – данные окружности, точка А - данная точка.
Примем щ1 и щ2 за базисные, тогда точка А при инверсии преобразуется в точку Аґ, Аґ О1А, и А преобразуется Аґґ, АґґО2А.
А, Аґ, Аґґ щ (О, ОА), щ – искомая окружность.
Построение.
Похожие работы
... , поскольку точки М и М’ входят в формулу равноправно, а для центра инверсии и бесконечно удаленной области все очевидно. 1.3. Формула инверсии в комплексно сопряженных координатах. Найдем формулу обобщенной инверсии при задании точек комплексными числами. Пусть точкам S, M и М’ соответствуют комплексные числа s, z и z’. По формуле скалярного произведения векторов . Коллинеарность точек S, M и ...
... сумму элементарных вертикальных стержней: и , (VI.15) магнитное поле которых в точке Р будет представлять алгебраическую сумму из составляющих Ii каждого элемента. Таким образом, любая шкала хронологии обращений геомагнитного поля, построенная по рисунку аномалий рифтовых хребтов по принципу Вайна и Мэтьюза, является лишь гипотезой и не может быть использована для палеомагнитной стратификации. ...
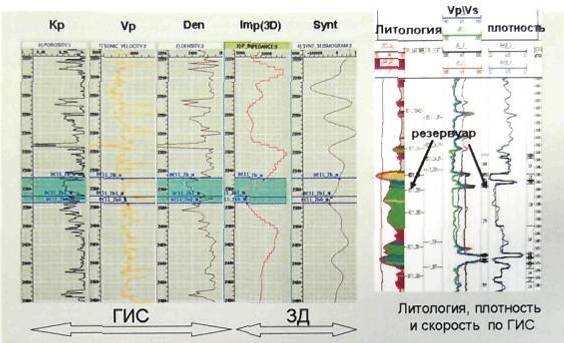
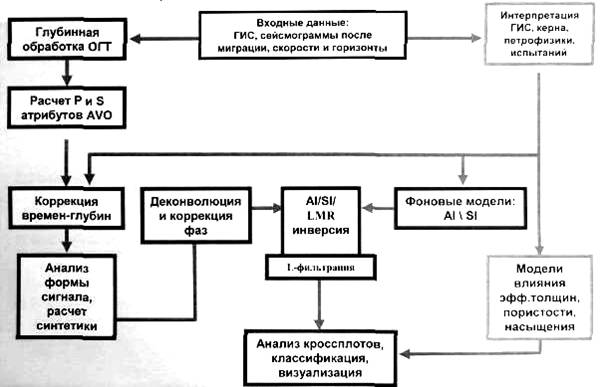
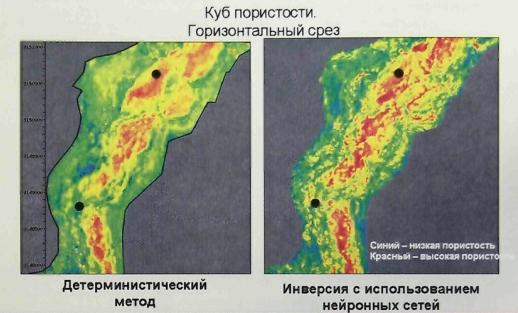
... PG) Нейронные алгоритмы Инверсия Log Prediction Neural Network Классификация сейсмофаций Stratimagic (патент TotalFinaElf) Волновое и геологическое представление геологического разреза Цель инверсии - перевести волновое представление сейсмических записей в пластовый вид, характерный для геологических разрезов. Если сравнить детальность по глубине кривых плотностного каротажа (слева - Den) ...
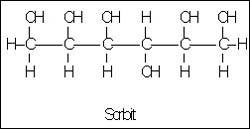
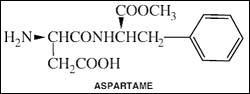
... сладости, чем сахар. Искусственные подсластители, как правило, низкокалорийны, что расширяет область их использования в пищевой промышленности. Кроме того, употребление таких заменителей сахара не вызывает кариеса, что обуславливает их широкое применение при производстве фармацевтических препаратов. Благодаря высокой сладости искусственные подсластители добавляются в продукцию в значительно ...
0 комментариев