Навигация
Дифференциальное уравнение вида
2. Дифференциальное уравнение вида
![]()
называется дифференциальным уравнением с разделёнными переменными.
Чтобы найти его общее решение, достаточно проинтегрировать обе его части.
![]() .
.
Дифференциальное уравнение вида
![]()
называется дифференциальным уравнением с разделяющимися переменными.
Чтобы найти его общее решение, надо сначала отделить переменные
![]()
а затем проинтегрировать
![]()
Пример 7.4. Найти общее решение уравнения
![]()
Решение. Сначала отделим переменные
![]()
![]() ,
,
а затем проинтегрируем
![]() ,
, ![]() ,
у=Сlnx.
,
у=Сlnx.
3. Функция ![]() называется однородной функцией п-го измерения относительно переменных х и у, если для произвольного числа
называется однородной функцией п-го измерения относительно переменных х и у, если для произвольного числа ![]() выполняется тождество
выполняется тождество
![]()
Пример 7.5.
1) ![]() =
=![]() ,
, ![]()
![]() - однородная функция третьего измерения.
- однородная функция третьего измерения.
2) ![]() =
=![]() - однородная функция нулевого измерения.
- однородная функция нулевого измерения.
Уравнение y’=![]() называется однородным дифференциальным уравнением первого порядка, если функция
называется однородным дифференциальным уравнением первого порядка, если функция ![]() является однородной функцией нулевого измерения, то есть, если
является однородной функцией нулевого измерения, то есть, если
![]() (7.2)
(7.2)
Очевидно, уравнение вида
![]()
будет однородным тогда и только тогда, когда функции Р(х,у) и Q(х,у), будут однородными функциями одного и того же измерения. Например, уравнение
![]()
однородное. Считая, в соотношении (7.2) ![]() , получим
, получим
![]()
Поэтому можно дать ещё одно определение однородного уравнения: однородным дифференциальным уравнением называется уравнение вида
![]() (7.3)
(7.3)
Применим в уравнении (7.3) подстановку
![]() ,
, ![]() ,
, ![]()
Тогда получим уравнение с разделяющимися переменными
![]() ,
,
которое всегда интегрируется в квадратурах:
![]() ,
,
![]() .
.
После интегрирования надо сделать обратную замену, то есть вместо и нужно подставить ![]()
Вывод. Однородные дифференциальные уравнения первого порядка всегда сводятся к уравнениям с разделяющимися переменными подстановкой ![]() ,
,![]() .
.
Пример 7.6. Найти общее решение уравнения
![]()
Решение. Применим подстановку ![]() ,
,![]() . Тогда получим
. Тогда получим
![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() .
.
Пример 7.7. Решить задачу Коши
![]() , у(1)=2.
, у(1)=2.
Решение. Поскольку обе функции
![]()
![]()
однородные измерения два, то данное уравнение однородное. Запишем его в виде
![]()
и применим подстановку ![]() ,
,![]() . Тогда получим
. Тогда получим
![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]() .
.
Из начального условия найдём постоянную интегрирования:
![]()
Подставив найденное значение С в общее решение, получим решение задачи Коши:
![]()
Лекция 16. Тема – Уравнения Бернулли. Комплексные числа. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
План.
1.Линейные дифференциальные уравнения первого порядка. Уравнения Бернулли.
2. Комплексные числа.
3. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
1. Линейным дифференциальным уравнением первого порядка называется уравнение вида
![]() (7.4)
(7.4)
где ![]() - известные функции переменной х.
- известные функции переменной х.
Термин «линейное уравнение» поясняется тем, что неизвестная функция у и её производная у’ входят в уравнение в первой степени, то есть линейно.
Линейное дифференциальное уравнение первого порядка всегда интегрируемо в квадратурах, поскольку его можно всегда свести к двум уравнениям с разделяющимися переменными таким образом (методом Бернулли).
Будем искать решение уравнения (7.4) в виде произведения
![]() (7.5)
(7.5)
где ![]() - неизвестные функции х. Находя производную
- неизвестные функции х. Находя производную
![]()
и подставляя значение у и у’ в уравнение (7.5), получим
![]() (7.6)
(7.6)
Выберем функцию ![]() так, чтобы выражение в скобках равнялось нулю. Для этого надо решить уравнение с разделяющимися переменными.
так, чтобы выражение в скобках равнялось нулю. Для этого надо решить уравнение с разделяющимися переменными.
![]()
Решая его, находим
![]()
![]() . (7.7)
. (7.7)
Постоянную интегрирования в выражении (7.7) не пишем, поскольку нам достаточно найти только какую-нибудь одну функцию ![]() , которая преобразовывает в ноль выражение в скобках в уравнении (7.6).
, которая преобразовывает в ноль выражение в скобках в уравнении (7.6).
Подставляя (7.7) в (7.6), получим
![]()
![]() (7.8)
(7.8)
Подставляя (7.7) и (7.8) в (7.5), найдём общее решение уравнения (7.4):
![]() (7.9)
(7.9)
Замечание. На практике помнить формулу (7.9) не обязательно: достаточно лишь помнить, что линейные дифференциальные уравнения первого порядка, а также уравнения Бернулли, решаются методом Бернулли с помощью подстановки ![]() .
.
Уравнением Бернулли называется уравнение вида
![]()
где ![]() - известные функции х,
- известные функции х, ![]() .
.
Похожие работы
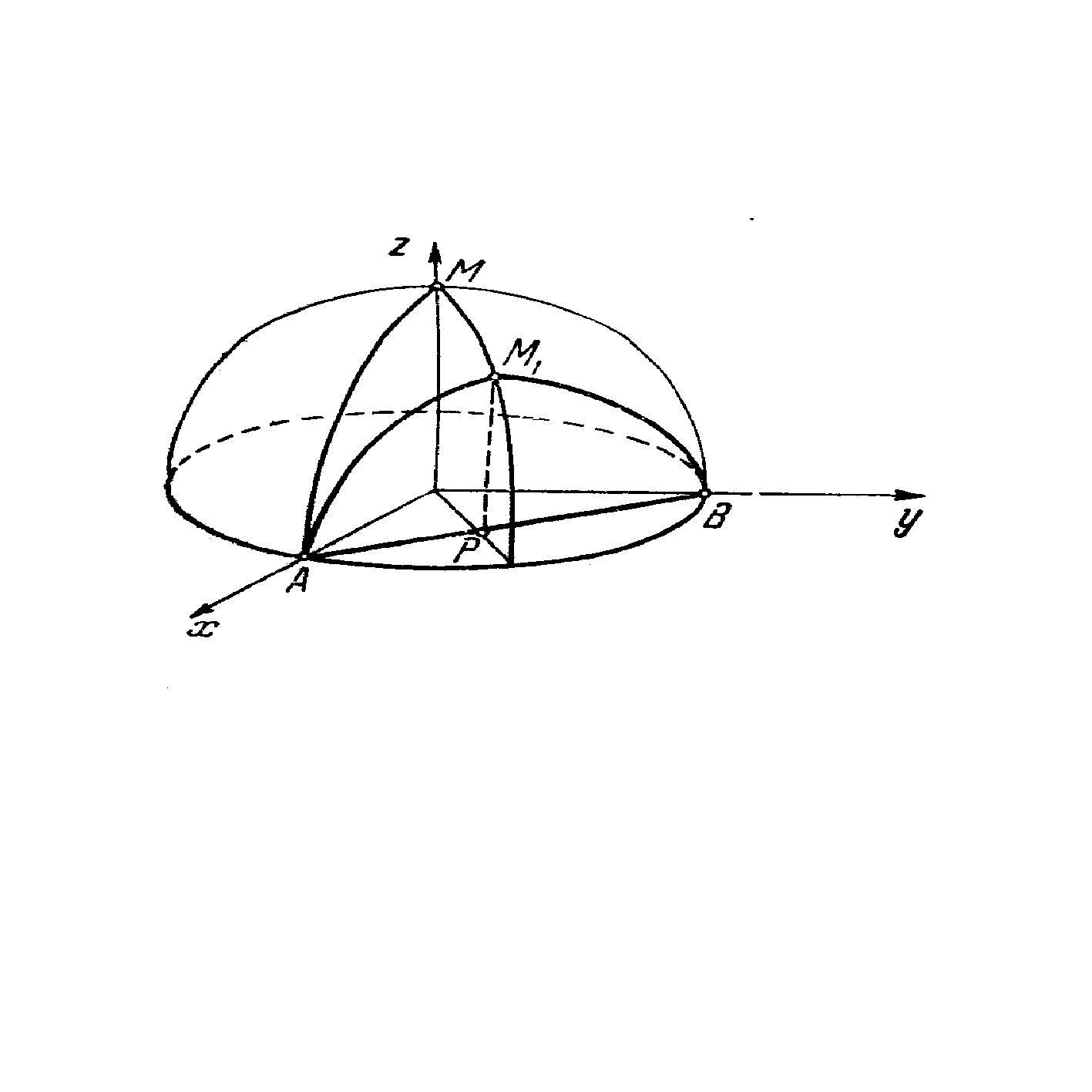
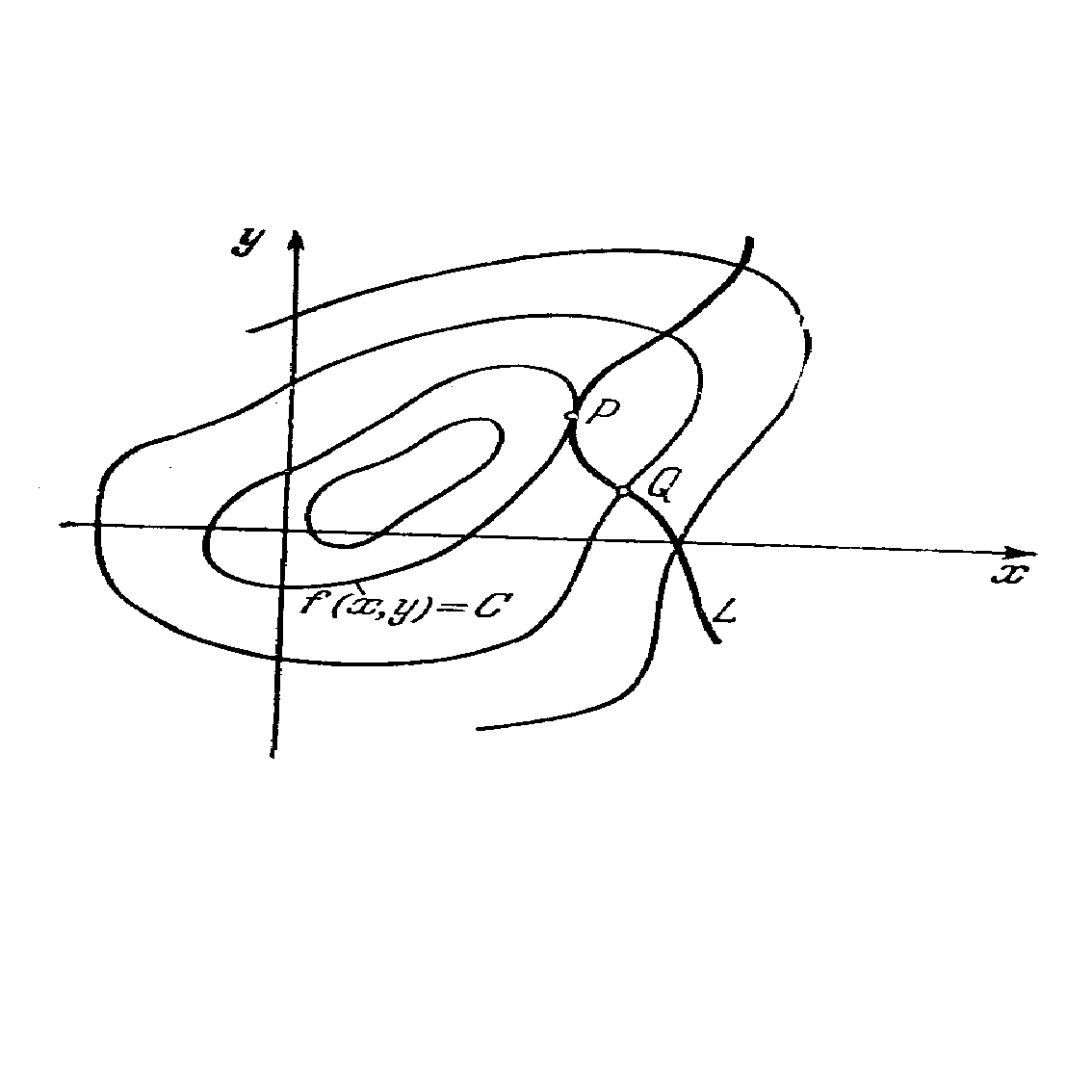
... (x, y) выполняется неравенство: . При этом, т. е. приращение функции > 0. Определение 3: Точки локальных минимума и максимума называются точками экстремума. Условные Экстремумы При отыскании экстремумов функции многих переменных часто возникают задачи, связанные с так называемым условным экстремумом. Это понятие можно разъяснить на примере функции двух переменных. Пусть заданы функция ...
... p и q, получим некоторые наборы (в зависимости от p и q) на которых функция достигает максимума. 3. Решение задачи с использованием метода покоординатного спуска 3.1 Описание метода покоординатного спуска Изложим этот метод на примере функции трех переменных . Выберем нулевое приближение . Фиксируем значения двух координат . Тогда функция будет зависеть только от одной переменной ; ...
... , Флетчера-Ривса). Методы второго порядка, использующие, кроме того, и информацию о вторых производных функции f (x) (метод Ньютона и его модификации). Метод конфигураций (Хука - Дживса) Следует выделить два этапа метода конфигураций: 1) исследование с циклическим изменением переменных и 2) ускорение поиска по образцам. Исследующий поиск начинается в точке х0, называемой старым базисом. ...
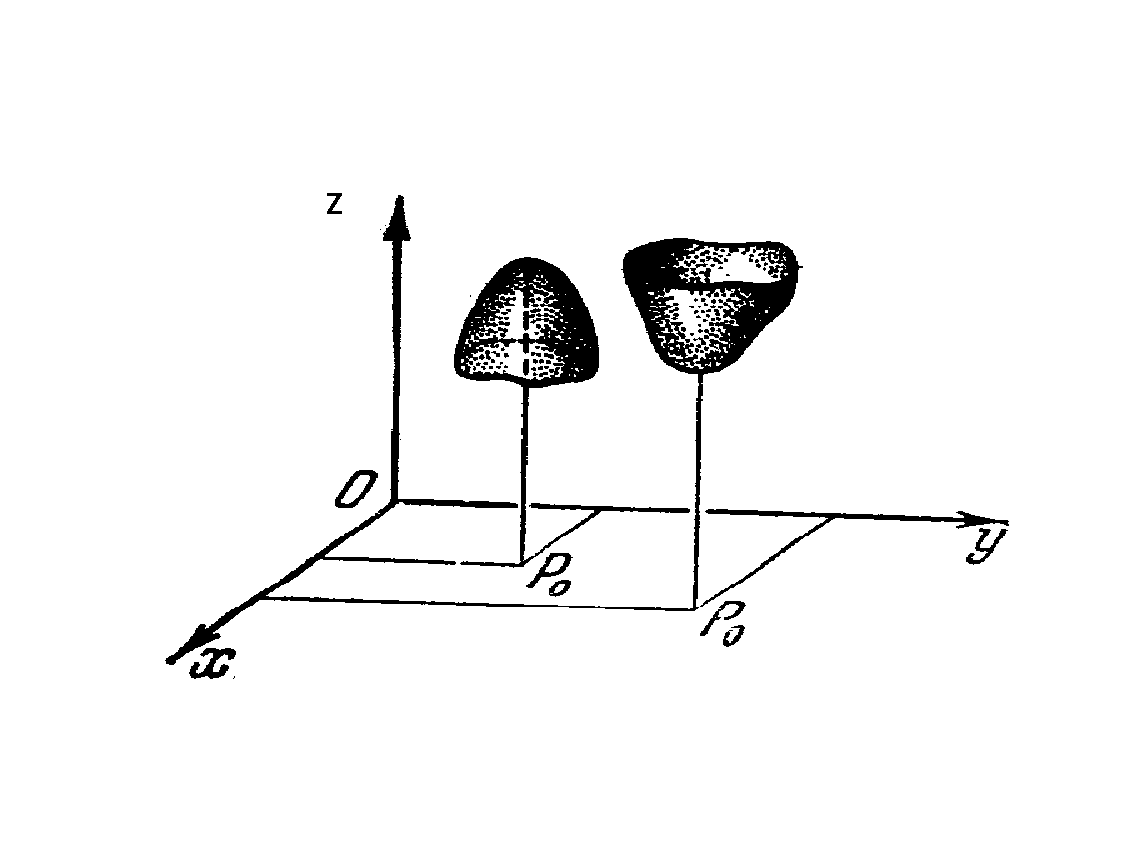
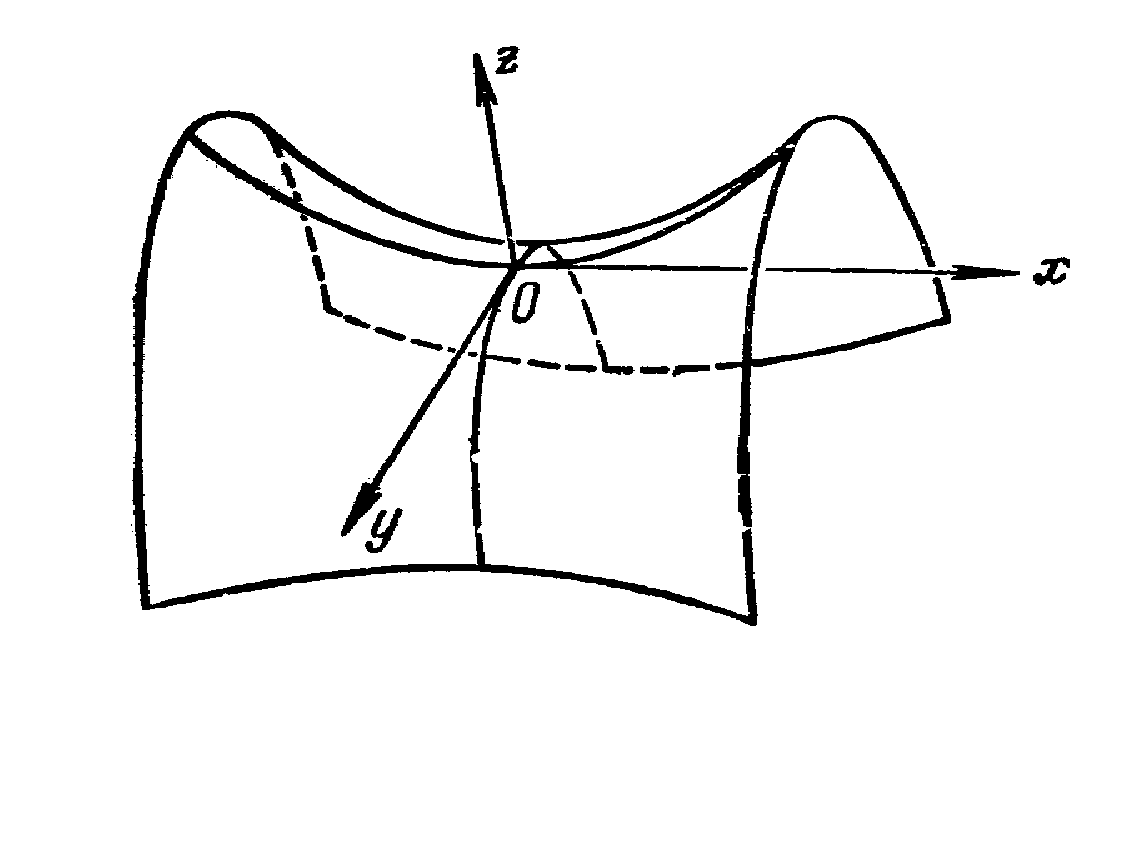
... , что и ошибки эксперимента, то итерации надо прекращать. Поскольку вблизи минимума чаще всего ~, то небольшая погрешность функции приводит к появлению довольно большой области неопределенности ~. 2. Минимум функции многих переменных 2.1 Рельеф функции Основные трудности многомерного случая удобно рассмотреть на примере функции двух переменных . Она описывает некоторую поверхность в ...







0 комментариев