Навигация
Производная в направлении вектора, перпендикулярного градиенту, равна нулю
2. Производная в направлении вектора, перпендикулярного градиенту, равна нулю.
3. Пусть функция z=f(x;у) определена на множестве D и точка М![]() (х
(х![]() ;у
;у![]() )
)![]() D. Если существует окрестность точки М
D. Если существует окрестность точки М![]() , которая принадлежит множеству D, и для всех отличных от М
, которая принадлежит множеству D, и для всех отличных от М![]() точек М выполняется неравенство
точек М выполняется неравенство
f(М)< f(М0) (f(М)> f(М0)),
то точку М![]() называют точкой локального максимума (минимума) функции z=f(x;у), а число f(М0) - локальным максимумом (минимумом) этой функции. Точки максимума и минимума функции называют её точками экстремума.
называют точкой локального максимума (минимума) функции z=f(x;у), а число f(М0) - локальным максимумом (минимумом) этой функции. Точки максимума и минимума функции называют её точками экстремума.
Теорема 5.1 (необходимые условия экстремума).
Если функция z=f(x;у) в точке М![]() ( х
( х![]() ;у
;у![]() ) имеет локальный экстремум, то в этой точке частные производные
) имеет локальный экстремум, то в этой точке частные производные ![]() ,
,![]() равны нулю или не существуют.
равны нулю или не существуют.
Точки, в которых ![]() =
=![]() = 0, называются стационарными. Стационарные точки и точки, в которых частные производные не существуют, называются критическими.
= 0, называются стационарными. Стационарные точки и точки, в которых частные производные не существуют, называются критическими.
Поэтому функция может достигать экстремальных значений только в критических точках; однако не всякая критическая точка является точкой экстремума.
Пусть в стационарной точке М![]() ( х
( х![]() ;у
;у![]() ) и некоторой её окрестности функция z=f(x;у) имеет непрерывные частные производные второго порядка. Введём обозначения:
) и некоторой её окрестности функция z=f(x;у) имеет непрерывные частные производные второго порядка. Введём обозначения:
А=![]() ( х
( х![]() ;у
;у![]() ), В=
), В=![]() ( х
( х![]() ;у
;у![]() ), С=
), С=![]() ( х
( х![]() ;у
;у![]() ),
), ![]() =АС-В2.
=АС-В2.
Теорема 5.2 (достаточные условия экстремума).
1. Если ![]() >0, то функция z=f(x;у) в точке М
>0, то функция z=f(x;у) в точке М![]() имеет экстремум, причём максимум при А<0 и минимум при А>0.
имеет экстремум, причём максимум при А<0 и минимум при А>0.
2. Если ![]() <0, то в точке М
<0, то в точке М![]() нет экстремума.
нет экстремума.
Для случая, когда количество переменных п>2, пользуются такой теоремой.
Теорема 5.3 Функция и= f(х![]() ;...;х
;...;х![]() ) имеет минимум в стационарной точке М
) имеет минимум в стационарной точке М![]() , если дифференциал второго порядка этой функции в точке М
, если дифференциал второго порядка этой функции в точке М![]() положителен d2f(М
положителен d2f(М![]() )>0, и максимум, если d2f(М
)>0, и максимум, если d2f(М![]() )<0.
)<0.
Пример. Исследовать на экстремум функцию
z=(х+2)2+(у -1)2.
Решение.

![]()
![]()
![]()
![]()
![]()
Функция имеет одну критическую точку М(-2;1).
![]()
![]()
![]() А=2, В=0,
С=2,
А=2, В=0,
С=2,
![]() =АС-В2= 2*2-02= 4>0, А>0.
=АС-В2= 2*2-02= 4>0, А>0.
Значит, в точке М(-2;1) функция имеет минимум: min z=z(-2;1)=(-2+2)2+(1-1)2=0.
Лекция 12. Тема – Интегральное исчисление функций. Первообразная. Неопределённный интеграл. Методы интегрирования.
План.
1. Первообразная функции. Неопределённный интеграл. Свойства неопределённого интеграла.
2. Таблица основных интегралов. Метод подстановки (замены переменной).
3. Интегрирование по частям. Интегралы, которые ”не берутся”.
Интеграл – одно из центральных понятий математики. Оно возникло в связи с двумя задачами: 1) о восстановлении функции по её производной; 2) о вычислении площади криволинейной трапеции. Эти задачи приводят к двум связанным между собой видам интегралов: определённого и неопределённого. Термин ”интеграл” ввёл Якоб Бернулли в 1690 году.
1. Функция F(x) называется первообразной функции f(x) на некотором промежутке, если во всех точках этого промежутка выполняется равенство F’(x)= f(x).
Например. первообразными функции f(x)=3х2 будут функции х3, х3+1, х3+0,5 и вообще F(x)= х3+С, где С – произвольная постоянная, поскольку F’(x)=( х3+С)’=3х2. Этот пример показывает, что если функция f(x) имеет одну первообразную, то она имеет их бесконечно много. Возникает вопрос: как найти все первообразные данной функции, если известна одна из них? Ответ даёт такая теорема.
Теорема 6.1 Если F(x) – первообразная функции f(x) на некотором промежутке, то всякая другая первообразная функции f(x) на этом промежутке имеет вид F(x) +С, где С – произвольная постоянная.
Множество всех первообразных F(x) +С функции f(x) называют неопределённым интегралом функции f(x) и обозначают ![]() . Таким образом, по определению
. Таким образом, по определению
![]() = F(x) +С, если F’(x)= f(x).
= F(x) +С, если F’(x)= f(x).
При этом f(x) называют подынтегральной функцией, f(x)dх – подынтегральным выражением, х – переменной интегрирования, знак ![]() - знаком интеграла, С – постоянной интегрирования.
- знаком интеграла, С – постоянной интегрирования.
Операцию нахождения первообразной функции f(x) называют интегрированием этой функции.
Операции дифференцирования и интегрирования являются обратными по отношению друг к другу.
Возникает вопрос: для каждой ли функции f(x) существует первообразная, а значит, и неопределённый интеграл? Оказывается не для каждой. Но справедлива такая
Теорема 6.2. Всякая непрерывная на промежутке [a;b] функция имеет на этом промежутке первообразную.
СВОЙСТВА НЕОПРЕДЕЛЁННОГО ИНТЕГРАЛА
1. (![]() )’= f(x).
)’= f(x).
2. ![]() = F(x) +С.
= F(x) +С.
3. d![]() = f(x)dх.
= f(x)dх.
4. ![]() =
=![]()
![]()
![]() .
.
5. Если ![]() = F(x) +С и и=
= F(x) +С и и=![]() - произвольная функция, которая имеет непрерывную производную, то
- произвольная функция, которая имеет непрерывную производную, то
![]() = F(и) +С.
= F(и) +С.
В частности,
![]() =
=![]() F(ax+b) +С.
F(ax+b) +С.
Из очень важного свойства 5 следует, что таблица интегралов остаётся верной независимо от того, является ли переменная интегрирования независимой переменной или произвольной дифференцированной функцией. Таким образом, из одной формулы можно получать много других.
Пример.
![]() =
=![]() +С
+С ![]()
![]() =
=![]() =
=![]() +С,
+С, ![]() =
=![]() =
=![]() +С,
+С, ![]() =
=![]()
![]() +С.
+С.
Похожие работы
... (x, y) выполняется неравенство: . При этом, т. е. приращение функции > 0. Определение 3: Точки локальных минимума и максимума называются точками экстремума. Условные Экстремумы При отыскании экстремумов функции многих переменных часто возникают задачи, связанные с так называемым условным экстремумом. Это понятие можно разъяснить на примере функции двух переменных. Пусть заданы функция ...
... p и q, получим некоторые наборы (в зависимости от p и q) на которых функция достигает максимума. 3. Решение задачи с использованием метода покоординатного спуска 3.1 Описание метода покоординатного спуска Изложим этот метод на примере функции трех переменных . Выберем нулевое приближение . Фиксируем значения двух координат . Тогда функция будет зависеть только от одной переменной ; ...
... , Флетчера-Ривса). Методы второго порядка, использующие, кроме того, и информацию о вторых производных функции f (x) (метод Ньютона и его модификации). Метод конфигураций (Хука - Дживса) Следует выделить два этапа метода конфигураций: 1) исследование с циклическим изменением переменных и 2) ускорение поиска по образцам. Исследующий поиск начинается в точке х0, называемой старым базисом. ...
... , что и ошибки эксперимента, то итерации надо прекращать. Поскольку вблизи минимума чаще всего ~, то небольшая погрешность функции приводит к появлению довольно большой области неопределенности ~. 2. Минимум функции многих переменных 2.1 Рельеф функции Основные трудности многомерного случая удобно рассмотреть на примере функции двух переменных . Она описывает некоторую поверхность в ...



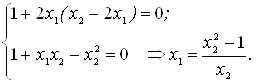




0 комментариев