Навигация
Методы оптимизации функций многих переменных
Кафедра: ИТ
МЕТОДЫ ОПТИМИЗАЦИИ ФУНКЦИЙ
МНОГИХ ПЕРЕМЕННЫХ
Екатеринбург 2007
Оглавление
Введение
Лабораторная работа № 1.
1. Методы безусловной оптимизации
1.1 Теоретический обзор. Исследование функции на безусловный экстремум
1.2 Численные методы минимизации функции
2. Порядок выполнения лабораторной работы
3. Пример выполнения лабораторной работы
4. Задания для лабораторного практикума
Лабораторная работа № 2.
1. Методы условной оптимизации
1.1 Теоретический обзор. Решение задачи минимизации со смешанными ограничениями
1.2 Седловые точки функции Лагранжа
1.3 Решение задач квадратичного программирования методом седловой точки
2. Порядок выполнения лабораторной работы
3. Пример выполнения лабораторной работы
4. Задания для лабораторного практикума
Библиографический список
Приложение
Введение
Настоящая работа является первой в серии методических указаний к лабораторным работам по дисциплинам "Методы оптимизации и нелинейное программирование" и "Методы оптимизации". Данные дисциплины читаются студентам 2-го курса специальности 230101 - Вычислительные машины, комплексы, системы и сети и направления 230100 - Информатика и вычислительная техника (бакалавры).
В указаниях рассматриваются задачи безусловной и условной нелинейной оптимизации. В теоретической части по каждой теме приводятся базовые понятия, теоремы и алгоритмы, которые потребуются для выполнения работ. Для выполнения графической и расчетной частей задач и реализации численных методов оптимизации студенты должны применить знание языков программирования и пакетов MATLAB, MATCAD, EXCEL. Выбор конкретного инструмента предоставляется самому студенту. Приведены примеры порядка выполнения и оформления лабораторных работ.
Проведенные вычисления, графические работы, анализ полученных результатов должны быть оформлены в виде отчета в соответствии со стандартными требованиями, предъявляемыми к отчетам и пояснительным запискам [1]. Сведения из теории, содержащиеся в данных методических указаниях, в отчет включать не рекомендуется.
Лабораторная работа № 1. 1. Методы безусловной оптимизации
Цель лабораторной работы - закрепление навыков исследования функций на выпуклость, решение задач на нахождение безусловного экстремума выпуклой функции аналитически и численными методами, изучение способов визуализации функций двух переменных в EXCEL и MATLAB.
1.1 Теоретический обзор. Исследование функции на безусловный экстремумРассматривается задача
f (x) → extr, x![]() Rn. (1)
Rn. (1)
Метод поиска безусловного экстремума основывается на следующих утверждениях:
Пусть функция f (x) дифференцируема в точке х*![]() Rn. Тогда если х*- локальное решение задачи (1), то
Rn. Тогда если х*- локальное решение задачи (1), то
grad f (x*) =0. (2)
Пусть функция f (x) дважды дифференцируема в точке х*![]() Rn. Тогда
Rn. Тогда
а) если х* - точка локального минимума в задаче (1), то матрица Гессе Н (х*) неотрицательно определена, т.е. ![]() р
р![]() Rn выполняется неравенство (Н (х*) р,р) ≥0;
Rn выполняется неравенство (Н (х*) р,р) ≥0;
б) если х* - точка локального минимума в задаче (1), то матрица Н (х*) неположительно определена, т.е. ![]() р
р![]() Rn выполняется неравенство (Н (х*) р,р) ≤0.
Rn выполняется неравенство (Н (х*) р,р) ≤0.
Пусть функция f (x) дважды дифференцируема в точке х*![]() Rn и
Rn и
grad f (x*) =0. Тогда
а) если матрица Н (х*) положительно определена, т.е. ![]() р
р![]() Rn, р≠0, (Н (х*) р,р) >0, то х* - точка строгого локального минимума функции f (x) на Rn;
Rn, р≠0, (Н (х*) р,р) >0, то х* - точка строгого локального минимума функции f (x) на Rn;
б) если матрица Н (х*) отрицательно определена, т.е. ![]() р
р![]() R, р≠0, (Н (х*) р,р) <0, то х* - точка строгого локального максимума функции f (x) на Rn.
R, р≠0, (Н (х*) р,р) <0, то х* - точка строгого локального максимума функции f (x) на Rn.
Если grad f (x*) =0, то х* называется стационарной точкой. Для выпуклой (вогнутой) на Rn функции стационарные точки являются точками ее глобального минимума (максимума). Строго выпуклые (вогнутые) функции имеют единственный глобальный минимум (максимум).
Критерий выпуклости функции. Дважды непрерывно дифференцируемая на выпуклом множестве Х с непустой внутренностью функция является выпуклой (вогнутой) на этом множестве в том и только том случае, когда матрица Гессе Н (х*) неотрицательно (не положительно) определена для всех х ![]() Х.
Х.
При исследовании на знакоопределенность матрицы вторых производных функции рекомендуется применять критерий Сильвестра или анализ собственных значений матрицы.
Схема поиска безусловных экстремумов функции:
Составить и решить систему алгебраических уравнений (2).
В стационарных точках (точках, являющихся решением системы (2)) исследовать на знакоопределенность матрицу вторых производных; точки, в которых Н (х) >0, являются точками глобального минимума; стационарные точки, в которых Н (х) <0, являются точками глобального максимума.
Исходя из вида исследуемой функции, проанализировать стационарные точки, в которых матрица вторых производных не является строго знакоопределенной.
Найденные точки локального экстремума исследуются на глобальный экстремум (если это возможно). В частности, если матрица Гессе неотрицательно (не положительно) определена на всем пространстве Еn, то все стационарные точки функции являются точками глобального минимума (максимума).
1.2 Численные методы минимизации функцииЧисленное решение задачи минимизации (1), как правило, связано с построением минимизирующей последовательности точек x0,x1,x2,…,xn,…, обладающих свойством
f (xk) <f (xk-1), k=0,1,… (3)
Общее правило построения минимизирующей последовательности имеет вид
x k+1=x k+t kd k, k=0,1,…,
где х0 - начальная точка поиска; dk - приемлемое направление перехода из точки xkв точку xk+1, которое обеспечивает выполнение условий (3) и называется направлением спуска; tk - величина шага. Начальная точка поиска задается исходя из физического содержания решаемой задачи и априорных данных о существовании и положении точек экстремума.
При решении вопроса о выборе численного метода рекомендуется оценить поведение линий уровня целевой функции в окрестностях предполагаемой точки экстремума. Число m = L/l, где L и l - максимальное и минимальное собственные значения гессиана функции f в предполагаемой точке экстремума x0 (характеризующее разброс собственных значений оператора f (x)), называется числом обусловленности гессиана функции f в точке x0. Если m >> 1, то функция f называется плохо обусловленной или овражной. Овражность, то есть вытянутость линий уровня вдоль одного направления, приводит к тому, что градиентные методы поиска экстремума функции сходятся медленно.
В зависимости от наивысшего порядка частных производных функции f (x), используемых для формирования dk и tk, численные методы принято делить на три группы:
Методы нулевого порядка, использующие информацию только о значениях функции f (x) (методы деформируемого многогранника, конфигураций). Эти методы могут применяться в тех случаях, когда функция задана неявно или не задана аналитически, но известен ряд значений функции или эти значения вычисляются непосредственно в ходе реализации алгоритма. Они также могут быть полезны в случаях, когда производные функции могут быть заданы аналитически, но их выражения очень громоздки.
Методы первого порядка, использующие информацию о значениях самой функции f (x) и ее первых производных (методы наискорейшего градиентного спуска, дробления шага, Гаусса-Зейделя, Флетчера-Ривса).
Методы второго порядка, использующие, кроме того, и информацию о вторых производных функции f (x) (метод Ньютона и его модификации).
Метод конфигураций (Хука - Дживса)
Следует выделить два этапа метода конфигураций:
1) исследование с циклическим изменением переменных и 2) ускорение поиска по образцам.
Исследующий поиск начинается в точке х0, называемой старым базисом. Направления поиска - координатные направления. По каждому направлению поочередно с шагом +t0 (-t0) проверяется выполнение условия (2) и в качестве нового базиса берется точка с координатами, полученными в результате удачных шагов из начальной точки по каждому направлению.
Направление от старого базиса к новому задает направление ускорения поиска: в качестве следующей точки минимизирующей последовательности проверяется точка y1=x0+l (x1-x0). Здесь l - ускоряющий множитель, задаваемый пользователем. Если полученная точка является удачной, то она берется в качестве следующей точки для исследования. В противном случае исследование ведется из точки x1.
Метод деформируемого многогранника (Нелдера - Мида).
При решении задачи поиска минимума функции f (x) методом Нелдера-Мида строится последовательность множеств из n+1 точек, которые являются вершинами выпуклого многогранника. На каждом последующем k+1-м шаге из системы точек xi (k), i=1, …,n+1, полученной на k-м шаге, выводится точка xh (k), в которой функция f (x) имеет наибольшее значение (худшая точка). Вместо xh (k) в систему вводится новая точка, выбираемая на отрезке прямой, проходящей через худшую точку и центр тяжести оставшихся n вершин многогранника:
xn+2=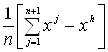 - центр тяжести;
- центр тяжести;
xn+3= xn+2+a (xn+2 - xh)
новая точка (“растянутое” отражение наихудшей вершины).
Метод дробления шага.
В данном методе строится релаксационная последовательность точек, т.е. таких точек {xk}, k=0,1,…, что f (xk) <f (xk-1), k=0,1,…. Точки последовательности {xk} вычисляются по следующему правилу:
xk+1=xk-tkgrad f (xk), k=0,1,… (4)
Начальная точка х0 и начальный шаг t0 задаются пользователем. Величина шага t0 не изменяется до тех пор, пока функция убывает в точках последовательности. Это контролируется путем проверки выполнения условия f (xk+1) - f (xk) <0 (или <-ε). Если условие убывания не выполняется, то величина шага уменьшается, как правило, вдвое, т.е. tk=tk/2.
Метод наискорейшего градиентного спуска
Как и в предыдущем методе, точки релаксационной последовательности {xk}, k=0,1,… вычисляются по правилу (4). Точка х0 задается пользователем; величина шага tk определяется из условия минимума одномерной функции φ (tk) =f (xk-tkgrad f (xk)). Задача минимизации функции φ (tk) может быть решена с использованием необходимого условия минимума ![]() =0 с последующей проверкой достаточного условия минимума
=0 с последующей проверкой достаточного условия минимума ![]() >0 или с использованием численных методов.
>0 или с использованием численных методов.
Метод сопряженных направлений (Флетчера - Ривса).
В данном методе используются свойства векторов, сопряженных относительно некоторой матрицы.
Определение. Векторы p и q называются сопряженными относительно матрицы Q, если выполняется равенство pQq=0.
Точки релаксационной последовательности {xk}, k=0,1,… вычисляются по правилу
xk+1=xk-tkdk, k=0,1,…;
dk = - grad f (xk) +βk-1 dk - 1; (5)
d0= - grad f (x0);
βk-1=║grad f (xk) ║2∕║grad f (xk-1) ║2.
Точка х0 задается пользователем; величина шага tk определяется из условия минимума функции φ (t) =f (xk-tdk). Задача минимизации одномерной функции φ (tk) может быть решена с использованием необходимого условия минимума ![]() =0 с последующей проверкой достаточного условия минимума
=0 с последующей проверкой достаточного условия минимума ![]() >0 или с использованием численных методов. Коэффициент βk-1вычисляется из условия сопряженности направлений dk и dk-1.
>0 или с использованием численных методов. Коэффициент βk-1вычисляется из условия сопряженности направлений dk и dk-1.
Метод Ньютона.
Строится последовательность точек {xk}, k=0,1,…, таких, что ![]() , k=0,1,… Точки последовательности {xk} вычисляются по правилу xk+1=xk+dk, k=0,1,… Точка х0 задается пользователем с учетом знакопостоянства и невырожденности матрицы Гессе в задаваемой начальной точке и близости выбранной точки к предполагаемой точке минимума. Направление спуска определяется для каждого значения k по формуле dk =-H-1 (xk) grad f (xk), где Н - матрица Гессе.
, k=0,1,… Точки последовательности {xk} вычисляются по правилу xk+1=xk+dk, k=0,1,… Точка х0 задается пользователем с учетом знакопостоянства и невырожденности матрицы Гессе в задаваемой начальной точке и близости выбранной точки к предполагаемой точке минимума. Направление спуска определяется для каждого значения k по формуле dk =-H-1 (xk) grad f (xk), где Н - матрица Гессе.
2. Порядок выполнения лабораторной работы
Записать необходимые условия экстремума. Аналитически или используя прикладные пакеты найти стационарные точки.
Проверить выполнение достаточных условий экстремума в найденных стационарных точках. Найти глобальный минимум функции. Оценить обусловленность задачи в точке минимума и овражность графика в окрестности точки минимума. Сделать предварительный вывод о работоспособности избранного численного метода.
Выбрать пакет, в котором будет строиться график. Рекомендации приведены в приложении. Построить график функции, задавая пределы изменения координат с учетом аналитически найденных точек минимума - максимума.
Выбрать несколько начальных точек для реализации численного метода. Задать критерий завершения итерационного процесса. Найти минимум. Сравнить результаты с аналитически найденным значением глобального минимума. Исследовать сходимость алгоритма, фиксируя точность определения минимума, количество итераций метода и количество вычислений минимизируемой функции в зависимости от задаваемой точности поиска. Результатом выполнения данного пункта должны быть выводы об объёме вычислений в зависимости от задаваемой точности и начального приближения.
3. Пример выполнения лабораторной работы[1]
Функция: ![]() min, x0= (-2,-2).
min, x0= (-2,-2).
Методы: градиентного спуска и Ньютона.
Решение: 1. Построим график функции и линии уровня (рис.1).
Примечание: при построении графика используется среда MathCAD.
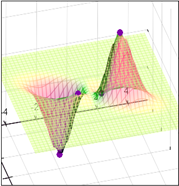
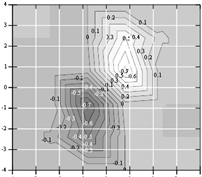
Рис.1. Графики функции ![]() и линий уровня
и линий уровня
Похожие работы
... , что и ошибки эксперимента, то итерации надо прекращать. Поскольку вблизи минимума чаще всего ~, то небольшая погрешность функции приводит к появлению довольно большой области неопределенности ~. 2. Минимум функции многих переменных 2.1 Рельеф функции Основные трудности многомерного случая удобно рассмотреть на примере функции двух переменных . Она описывает некоторую поверхность в ...
... от года-x и от номера месяца в году-y следующим образом: F(x)=50-x2+10x-y2+10y. Определите, в каком году и в каком месяце прибыль была максимальной. Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МЕТОДЫ ОПТИМИЗАЦИИ Билет № 22 1) Постановка вариационной задачи с ограничениями. Привести пример. 2) Дайте геометрическую ...
... Метод преобразования целевой функции, метод штрафных функций, табличный симплекс – метод. Список используемой литературы 1. А.Г.Трифонов. Постановка задачи оптимизации и численные методы ее решения; 2. Б. Банди. Методы оптимизации. Вводный курс., 1988; 3. Мендикенов К.К. Лекции Приложение А using System; using System.Collections.Generic; using System.ComponentModel; using System. ...
... переменных, доставляющих экстремум линейной целевой функции при m ограничениях в виде линейных равенств или неравенств. Линейное программирование представляет собой наиболее часто используемый метод оптимизации. К числу задач линейного программирования можно отнести задачи: · рационального использования сырья и материалов; задачи оптимизации раскроя; · оптимизации производственной программы ...








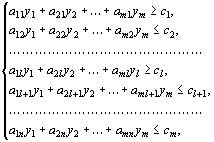

0 комментариев