Навигация
Если т и М – соответственно наименьшее и наибольшее значения функции f(x), на отрезке [a;b], то
8. Если т и М – соответственно наименьшее и наибольшее значения функции f(x), на отрезке [a;b], то
т(b-a) ![]()
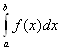
![]() M(a-b).
M(a-b).
9. (теорема о среднем значении функции).
Если функция f(x) непрерывна на отрезке [a;b], то на этом отрезке существует такая точка с, что 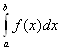 = f(с) (b-a).
= f(с) (b-a).
Число f(с)=![]()
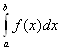 называют средним значением функции f(x) на отрезке [a;b].
называют средним значением функции f(x) на отрезке [a;b].
3. Пусть функция у= f(x) непрерывна на отрезке [a;b]. Тогда она интегрируема на любом отрезке [a;х]![]() [a;b], то есть для произвольного х
[a;b], то есть для произвольного х![]() [a;b] существует интеграл
[a;b] существует интеграл 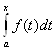 , который, очевидно, является функцией от х. Обозначим эту функцию через Ф(х)
, который, очевидно, является функцией от х. Обозначим эту функцию через Ф(х)
Ф(х)= 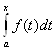 (6.3)
(6.3)
и назовём интегралом с переменным верхним пределом.
Теорема 6.4. Если функция f(x) непрерывна на отрезке [a;b], то интеграл (6.3) является дифференцированной функцией на этом отрезке, причём Ф’(х)=f(x).
Другими словами, интеграл с переменным верхним пределом является одной из первообразных подынтегральной функции f(x).
Пусть функция у= f(x) непрерывна на отрезке [a;b] и F(x) – первообразная функции f(x). Поскольку функция Ф(х) = 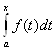 также является
первообразной функции f(x), а две первообразные одной функции отличаются только постоянным слагаемым, то
также является
первообразной функции f(x), а две первообразные одной функции отличаются только постоянным слагаемым, то
Ф(х)= F(x) +С, или 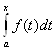 = F(x)+С. (6.4)
= F(x)+С. (6.4)
Считая в (6.4) х=а, получим
 =0= F(а)+С
=0= F(а)+С![]() С=- F(а).
С=- F(а).
Равенство (6.4) можно записать в виде
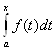 = F(x) - F(а).
= F(x) - F(а).
Заменим х на b и t на x. Получим формулу
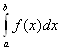 = F(b) - F(а),
= F(b) - F(а),
которая называется формулой Ньютона-Лейбница. Часто её записывают в виде
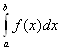 = F(x)
= F(x)![]() .
.
Формула Ньютона-Лейбница даёт удобный способ вычисления определённых интегралов.
Если функция и=и(х), v=v(x) и их производные и’(х), v’(x) непрерывны на отрезке [a;b], то справедлива формула интегрирования по частям
![]() =uv
=uv![]() -
-![]() .
.
Если функция f(x) непрерывна на отрезке [a;b], а функция х=![]() и её производная х’=
и её производная х’=![]() непрерывны на отрезке [a;b], причём
непрерывны на отрезке [a;b], причём ![]() ,
, ![]() , то справедлива формула
, то справедлива формула
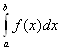 =
= .
.
Заметим, что, в отличие от неопределённого интеграла, в определённом интеграле нет необходимости делать обратную замену, поскольку появляются новые пределы интегрирования.
При определении определённого интеграла
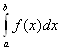
как предела интегральных сумм предусматривалось, что: 1) отрезок интегрирования [a;b] конечный и 2) подынтегральная функция f(x) на этом отрезке ограничена. Такой интеграл называется собственным, хотя слово «собственнный», как правило, опускается.
Если же хотя бы одно из двух приведенных условий нарушается, то интеграл называют несобственным. Различают два вида несобственных интеграла.
1. Несобственные интегралы с бесконечными пределами интегрирования
(несобственные интегралы І рода).
Если функция f(x) непрерывна при ![]() , то считают
, то считают
 =
=![]()
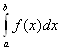 (6.5)
(6.5)
и в зависимости от существования или не существования конечного предела в правой части формулы (6.5) несобственный интеграл І рода  называют сходящимся или расходящимся. Аналогично
называют сходящимся или расходящимся. Аналогично
![]() =
=![]()
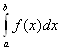 ,
, ![]() =
=![]()
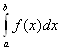 .
.
Похожие работы
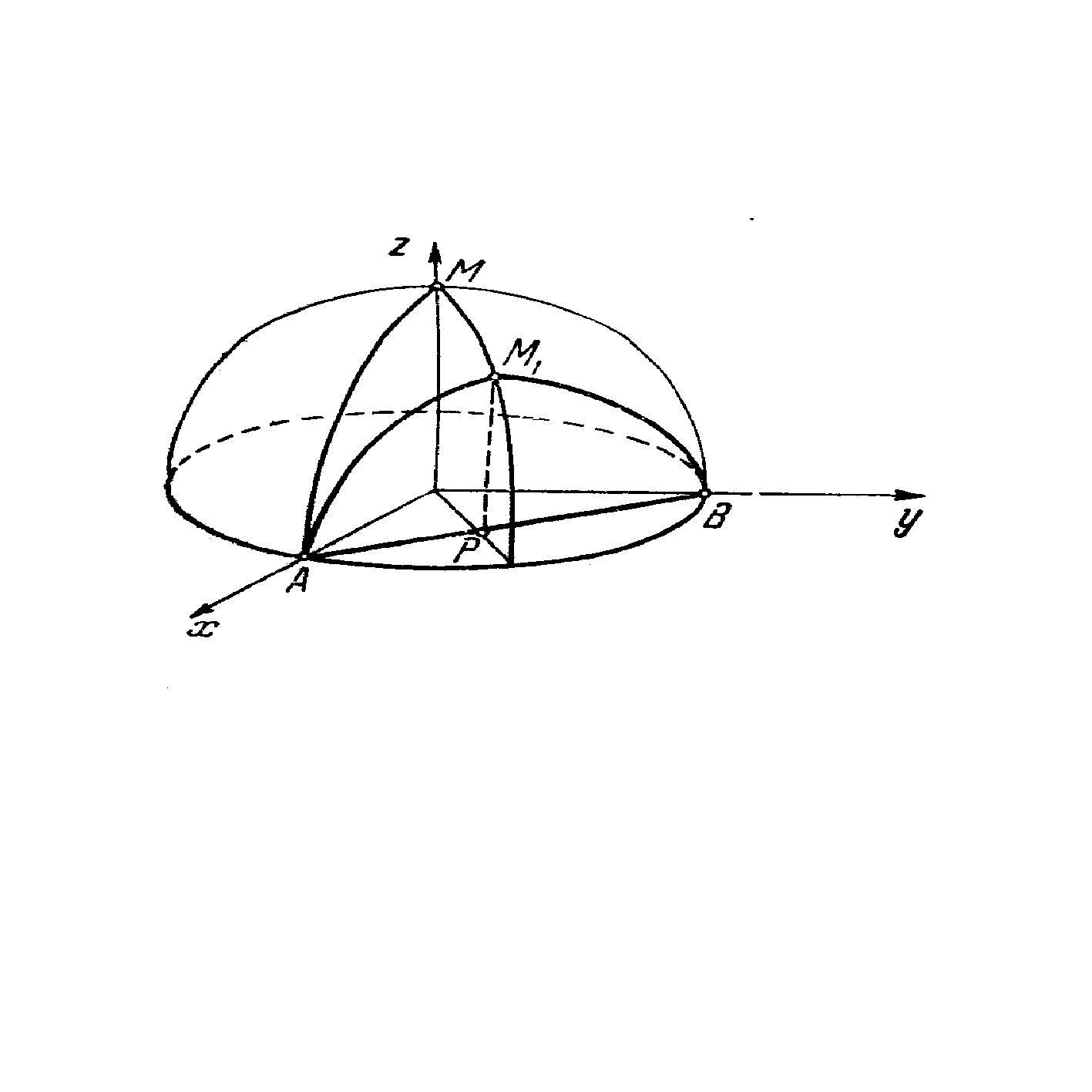
... (x, y) выполняется неравенство: . При этом, т. е. приращение функции > 0. Определение 3: Точки локальных минимума и максимума называются точками экстремума. Условные Экстремумы При отыскании экстремумов функции многих переменных часто возникают задачи, связанные с так называемым условным экстремумом. Это понятие можно разъяснить на примере функции двух переменных. Пусть заданы функция ...
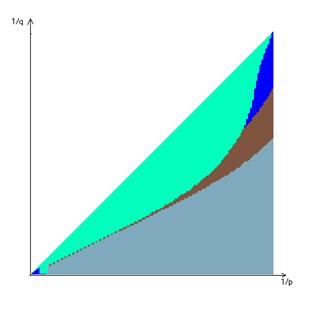
... p и q, получим некоторые наборы (в зависимости от p и q) на которых функция достигает максимума. 3. Решение задачи с использованием метода покоординатного спуска 3.1 Описание метода покоординатного спуска Изложим этот метод на примере функции трех переменных . Выберем нулевое приближение . Фиксируем значения двух координат . Тогда функция будет зависеть только от одной переменной ; ...
... , Флетчера-Ривса). Методы второго порядка, использующие, кроме того, и информацию о вторых производных функции f (x) (метод Ньютона и его модификации). Метод конфигураций (Хука - Дживса) Следует выделить два этапа метода конфигураций: 1) исследование с циклическим изменением переменных и 2) ускорение поиска по образцам. Исследующий поиск начинается в точке х0, называемой старым базисом. ...
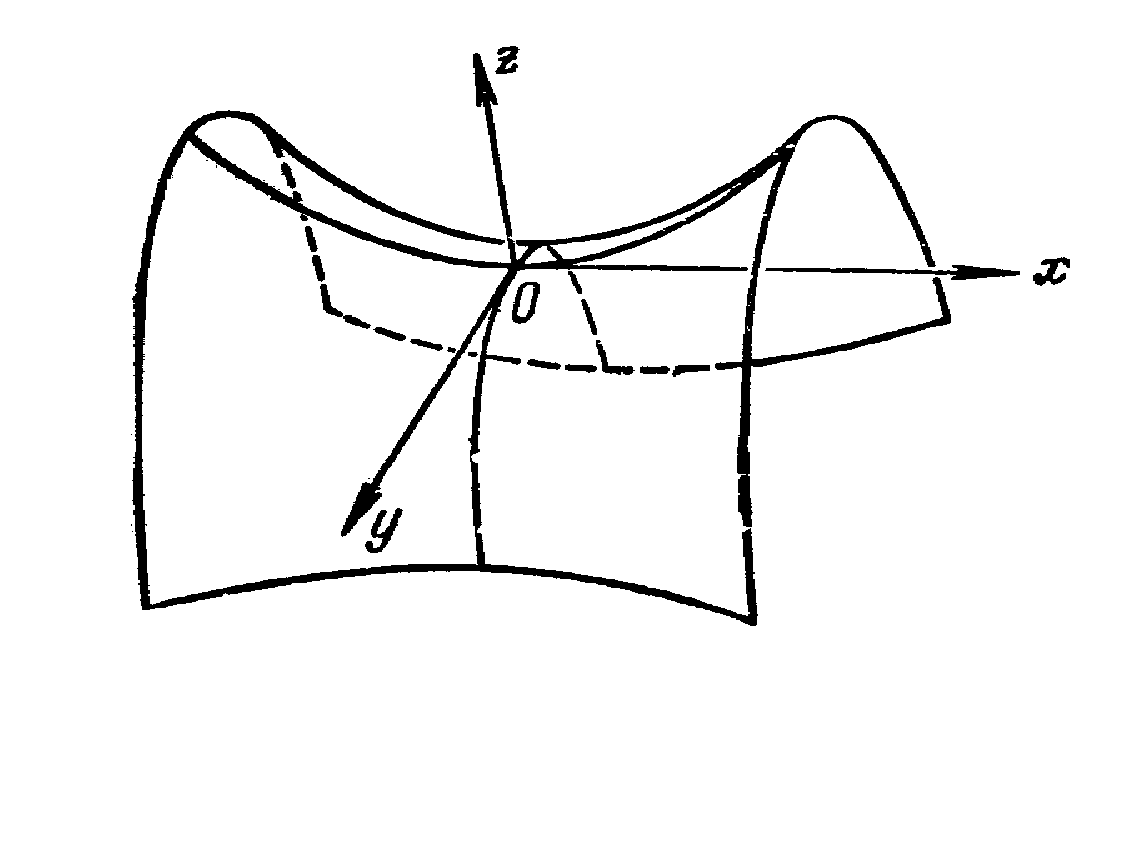
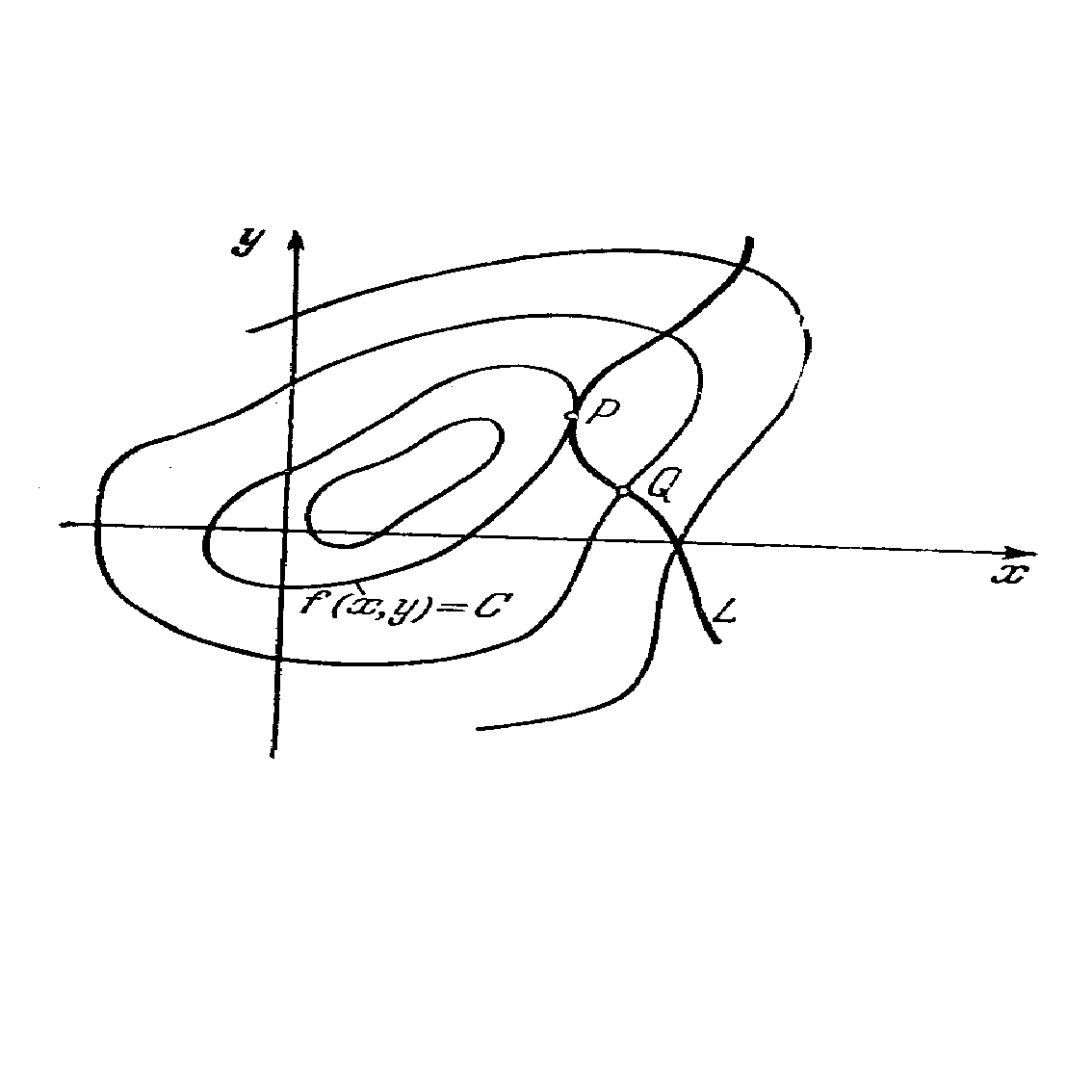
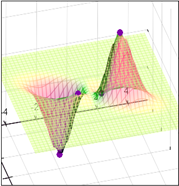
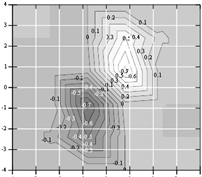
... , что и ошибки эксперимента, то итерации надо прекращать. Поскольку вблизи минимума чаще всего ~, то небольшая погрешность функции приводит к появлению довольно большой области неопределенности ~. 2. Минимум функции многих переменных 2.1 Рельеф функции Основные трудности многомерного случая удобно рассмотреть на примере функции двух переменных . Она описывает некоторую поверхность в ...



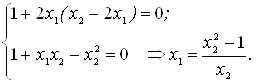




0 комментариев