Навигация
МАТЕМАТИЧЕСКИЕ МОДЕЛИ АСИНХРОННОЙ МАШИНЫ
3. МАТЕМАТИЧЕСКИЕ МОДЕЛИ АСИНХРОННОЙ МАШИНЫ
3.1 Математическое описание обобщённой машины
Обобщённая асинхронная машина содержит трёхфазную обмотку на роторе и статоре. Обмотки подключены к симметричным источникам напряжения. Математическое описание такой машины базируется на известных законах.
Уравнения равновесия ЭДС на обмотках статора и ротора базируется на втором законе Кирхгофа.
Для статора: Для ротора:
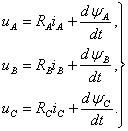
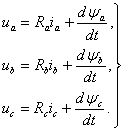 (3.1)
(3.1)
В уравнениях (3.1) фигурируют мгновенные напряжения, токи и потокосцепления статора и ротора, а также активные сопротивления обмоток. Обычно обмотки выполняются симметричными, к поэтому RА=RВ=RС=Rs - активное сопротивление статорной обмотки, Rа=Rb=Rс=RR - активное сопротивление роторной обмотки.
Вторым используемым законом является закон Ампера, который связывает потокосцепления обмоток с токами, протекающими по обмоткам:
Для статора:
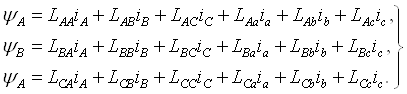 (3.2 а)
(3.2 а)
Для ротора:
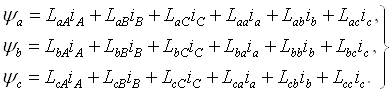 (3.2 б)
(3.2 б)
Удивительно симметричные уравнения для определения потокосцеплений показывают, что потокосцепление каждой обмотки зависит от токов во всех обмотках; эти зависимости проявляются через взаимоиндукцию. В уравнениях (3.2) LАА, LBB, LCC, Laa, Lbb, Lcc, являются собственными индуктивностями соответствующих обмоток, все остальные - взаимоиндуктивностями между соответствующими обмотками.
Третьим законом, лежащим в основе анализа, является второй закон Ньютона - закон равновесия моментов на валу машины:
![]() (3.3)
(3.3)
где J (кг×м2) - момент инерции на валу машины, учитывающий инерционность как самой машины, так и приведенной к валу инерционности рабочего механизма и редуктора, ![]() - угловая скорость вала машины,
- угловая скорость вала машины, ![]() (Н×м) - момент рабочего механизма, приведенный к валу, в общем случае он может быть функцией скорости и угла поворота,
(Н×м) - момент рабочего механизма, приведенный к валу, в общем случае он может быть функцией скорости и угла поворота, ![]() .
.
Наконец, четвертым и последним законом, лежащим в основа анализа машины, является закон, сформулированный Ленцем, как правило левой руки. Этот закон связывает векторные величины момента, потокосцепления и тока:
![]() .(3.4)
.(3.4)
Следует сразу подчеркнуть, что, несмотря на полное и строгое математическое описание, использование уравнений (3.1) - (3.4) для исследования машины встречает серьезные трудности. Из них основные:
- в уравнениях (3.3 и 3.4) фигурируют векторные величины, а в уравнениях (3.1 и 3.2) скалярные;
- количество взаимосвязанных уравнений равно 16, а количество коэффициентов - 44;
- коэффициенты взаимоиндукции между обмотками статора и ротора в уравнениях (3.2) являются функцией угла поворота ротора относительно статора, то есть уравнения (3.2) являются уравнениями с переменными коэффициентами;
- уравнение (3.4) является нелинейным, так как в нем перемножаются переменные.
3.2 Метод пространственного вектора
На пути упрощения математического описания асинхронной машины, да и вообще всех машин переменного тока, удивительно удачным и изящным оказался метод пространственного вектора, который позволил существенно упростить и сократить вышеприведенную систему уравнений; метод позволяет связать уравнения (3.1-3.4) в единую систему с векторными переменными состояния. Суть метода состоит в том, что мгновенные значения симметричных трехфазных переменных состояния (напряжения, токи, потокосцепления) можно математически преобразовать так, чтобы они были представлены одним пространственным вектором. Это математическое преобразование имеет вид (например, для тока статора):
![]() (3.5)
(3.5)
где ![]() - векторы, учитывающие пространственное смещение обмоток,
- векторы, учитывающие пространственное смещение обмоток, ![]() - симметричная трехфазная система токов статора.
- симметричная трехфазная система токов статора.
Подставив в уравнения (3.5) значение мгновенных токов, найдем математическое описание пространственного вектора статорного тока:
![]() (3.6)
(3.6)
На рис. 3.1 представлена геометрическая интерпретация пространственного вектора тока - это вектор на комплексной плоскости с модулем (длиной) Im, вращающийся с угловой скоростью w в положительном направлении. Проекции вектора ![]() на фазные оси А, В, С определяют мгновенные токи в фазах. Аналогично пространственными векторами можно представить все напряжения, токи и потокосцепления, входящие в уравнения (3.1), (3.2).
на фазные оси А, В, С определяют мгновенные токи в фазах. Аналогично пространственными векторами можно представить все напряжения, токи и потокосцепления, входящие в уравнения (3.1), (3.2).
Теперь можно переходить к упрощению уравнений.
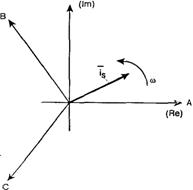
Рисунок 3.1 - Пространственный вектор тока
Шаг первый. Для преобразования уравнений (3.1) в мгновенных значениях к уравнениям в пространственных векторах умножим их на выражения: первые уравнения на ![]() , вторые – на
, вторые – на ![]() , третьи – на
, третьи – на ![]() , - и сложим раздельно для статора и ротора. Тогда получим:
, - и сложим раздельно для статора и ротора. Тогда получим:
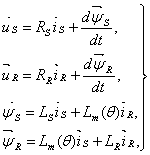 (3.7)
(3.7)
где LS, LR - собственные индуктивности статора и ротора, Lm(q) -взаимная индуктивность между статором и ротором. Таки образом, вместо двенадцати уравнений (3.1)-(3.2) получено лишь четыре уравнения (3.7).
Шаг второй. Переменные коэффициенты взаимной индукции уравнениях для потокосцеплений (3.7) являются результатом того, что уравнения равновесия ЭДС для статора записаны в неподвижно системе координат, связанной со статором, а уравнения равновесия ЭДС для ротора записаны во вращающейся системе координат, связанной с ротором. Метод пространственного вектора позволяет записать эти уравнения в единой системе координат, вращающейся произвольной скоростью wк. В этом случае уравнения (3.7) преобразуются к виду:
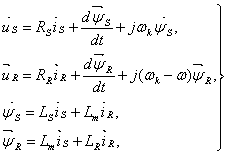 (3.8)
(3.8)
где w = р•wm, р - число пар полюсов в машине.
В уравнениях (3.8) все коэффициенты являются величинами постоянными, имеют четкий физический смысл и могут быть определены по паспортным данным двигателя, либо экспериментально.
Шаг третий. Этот шаг связан с определением момента. Момент в уравнении (3.4) является векторным произведением любой пары векторов. Из уравнения (3.8) следует, что таких пар может быть шесть ![]() . Часто в рассмотрение вводится потокосцепление взаимной индукции
. Часто в рассмотрение вводится потокосцепление взаимной индукции ![]() . В этом случае появляется ещё четыре возможности представления электромагнитного момента машины через следующие пары:
. В этом случае появляется ещё четыре возможности представления электромагнитного момента машины через следующие пары: ![]() . После выбора той или иной пары уравнение момента приобретает определенность, а количество уравнений в системе (3.8) сокращается до двух. Кроме того, в уравнениях (3.3) и (3.4) векторные величины момента и скорости могут быть заменены их модульными значениями. Это является следствием того, что пространственные векторы токов и потокосцеплений расположены и плоскости, перпендикулярной оси вращения, а векторы момента и угловой скорости совпадают с осью. В качестве примера запись уравнений момента через некоторые пары переменных состояния машины имеет вид:
. После выбора той или иной пары уравнение момента приобретает определенность, а количество уравнений в системе (3.8) сокращается до двух. Кроме того, в уравнениях (3.3) и (3.4) векторные величины момента и скорости могут быть заменены их модульными значениями. Это является следствием того, что пространственные векторы токов и потокосцеплений расположены и плоскости, перпендикулярной оси вращения, а векторы момента и угловой скорости совпадают с осью. В качестве примера запись уравнений момента через некоторые пары переменных состояния машины имеет вид:
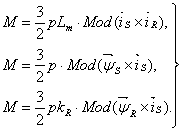 (3.9)
(3.9)
В конечном виде уравнения обобщённой асинхронной машины имеют вид:
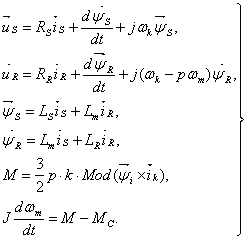 (3.10)
(3.10)
Похожие работы
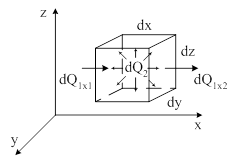
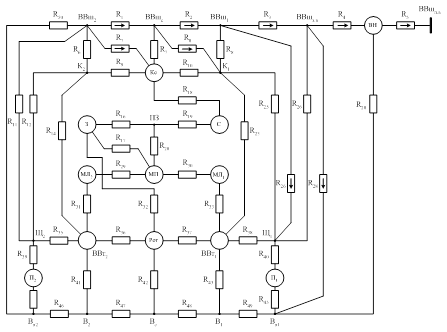
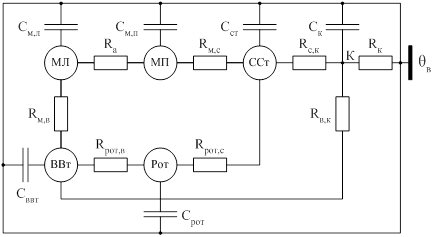
... тепловой схемы выполнялось для стационарного режима, так как коэффициенты теплоотдачи в переходном и стационарном режимах одинаковы. Полученные результаты используются в компьютерной лабораторной работе «Моделирование нагрева асинхронного двигателя в различных режимах работы». Лабораторная работа выполнена в программной среде MatLab 6.1, и в ее приложении Simulink 4. Данная работа позволяет ...


0 комментариев