Навигация
Понятия языка Лисп
2.2 Понятия языка Лисп.
2.2.1 Атомы и списки.Основная структура данных в Лиспе - символьные или S-выражения, которые определяются как атомы или списки.
Символы и числа представляют собой те объекты Лиспа, из которых строятся остальные структуры. Поэтому их называют атомами.
Символ - это имя, состоящее из букв, цифр и специальных знаков, которое обозначает какой-нибудь предмет, объект, действие из реального мира. В Лиспе символы обозначают числа, другие символы или более сложные структуры, программы (функции) и другие лисповские объекты.
Пример: х, г-1997, символ, function.
Числа не являются символами, так как число не может представлять иные лисповские объекты, кроме самого себя, или своего числового значения. В Лиспе используется большое количество различных типов чисел (целые, десятичные и т. д.) - 24, 35.6, 6.3 e5.
Символы T и NIL имеют в Лиспе специальное назначение: T обозначает логическое значение истина, а NIL - логическое значение ложь. Символы T и NIL имеют всегда одно и тоже фиксированное встроенное значение. Их нельзя использовать в качестве имен других лисповских объектов. Символ NIL обозначает также и пустой список.
Числа и логические значения T и NIL являются константами, остальные символы - переменными, которые используются для обозначения других лисповских объектов.
Список - это упорядоченная последовательность, элементами которой являются атомы или списки (подсписки). Списки заключаются в круглые скобки, элементы списка разделяются пробелами. Открывающие и закрывающие скобки находятся в строгом соответствии. Список всегда начинается с открывающей и заканчивается закрывающей скобкой. Список, который состоит из 0 элементов называют пустым и обозначают () или NIL. Пустой список - это атом. Например: (а в (с о) р), (+ 3 6).
Число T, NIL Списки
Константы
Атомы
S-выражения
Рис.2 Символьные выражения. 2.2.2 Внутреннее представление списка.
Оперативная память машины логически разбивается на маленькие области, называемые списочными ячейками. Списочная ячейка состоит из двух частей, полей CAR и CDR (головы и хвоста соответственно). Каждое из полей содержит указатель. Указатель может ссылаться на другую списочную ячейку или на другой лисповский объект, например, атом. Указатели между ячейками образуют как бы цепочку, по которой можно из предыдущей ячейки попасть в следующую и так до атомарных объектов. Каждый известный системе атом записан в определенном месте памяти лишь один раз. Указателем списка является указатель на первую ячейку списка. На одну и ту же ячейку может указывать несколько указателей, но исходить только один.
Графически списочная ячейка представляется прямоугольником (рис3), разделенным на части CAR и CDR. Указатель изображается в виде стрелки, начинающейся в одной из частей прямоугольника и заканчивающейся на изображении другой ячейки или атоме, на которые ссылается указатель.
Рис.3 Списочная ячейка.
Логически идентичные атомы содержатся в системе лишь один раз. Но логически идентичные списки могут быть представлены различными списочными ячейками. Например, список ((d c) a d c) изображается как показано на рис.4. В результате вычислений в памяти могут возникнуть структуры на которые нельзя потом сослаться. Это происходит, если структуры не сохранены с помощью функции SETQ или теряется ссылка на старое значение в связи с новым переприсваиванием.
A D C
Рис.4
A D C
рис.5
В зависимости от способа построения логическая и физическая структуры двух списков могут оказаться различными. Например, список ((d c) a d c) может иметь и другую структуру (рис5). Логическая структура всегда топологически имеет форму двоичного дерева, в то время как физическая структура может быть ациклическим графом, т. е. ветви могут снова сходиться, но никогда не могут образовывать замкнутые циклы (указывать назад).
При логическом сравнивании списков используют предикат EQUAL, сравнивающий не физические указатели, а совпадение структурного построения списков и совпадение атомов, формирующих список.
Предикат EQ можно использовать лишь для сравнения двух символов. Во многих реализациях Лиспа этот предикат обобщен таким образом, что с его помощью можно определить физическое равенство двух выражений (т. е. ссылаются ли значения аргументов на один физический лисповский объект) не зависимо от того, является ли он атомом или списком.
2.2.3 Написание программы на Лиспе.
Любая Лисп-система представляет собой небольшую программу, назначение которой - выполнение программ путем интерпретации S-выражений, подаваемых на вход. Механизм работы Лисп-системы очень прост. Он состоит из трех последовательных шагов: считывание S-выражения; интерпретация S-выражения; печать S-выражения.
Обычно, написание программы на Лиспе - написание некоторой функции, возможно весьма сложного вида, при вычислении использующей какие-либо другие функции или рекурсивно саму себя. Однако на практике часто оказывается, что более удобно решать задачи путем выполнения последовательности отдельных более или менее простых шагов с сохранением и дальнейшим использованием промежуточных результатов. Шагом в нашем случае будет вычисление некоторой функции Лиспа. Разрешая использовать переменные не только в качестве аргументов функций, мы расстаемся с чистотой функционального программирования, но вместе с тем приобретаем инструмент, в ряде случаев облегчающий написание программ и нередко повышающий эффективность их работы на ВМ с традиционной архитектурой. Наиболее широко в практическом программировании на Лиспе распространен смешанный стиль программирования: программу стараются писать функционально, но при этом соответствующие функции не делают слишком сложными, переходя везде, где это облегчает написание соответствующей функции и понимание принципа ее работы, к императивному (второму) методу программирования.
Итак, как правило, программа написанная на Лиспе, представляет собой последовательность вызовов некоторых функций, как встроенных в Лисп, так и предварительно описанных самим пользователем, а средством связи между последовательно вызываемыми функциями являются переменные, позволяющие запомнить любой объект (атом, список, точечную пару).
Все Лисп-системы имеют некоторый набор базовых функций (их мы рассмотрим в лабораторных работах), которые изначально встроены в интерпретатор. Кроме того, пользователь может определять свои собственные функции на языке Лисп, используя специальные конструкторы функций. Если атом f не удается интерпретировать как встроенную функцию языка или как функцию, определенную пользователем, большинство интерпретаторов выдают сообщение об ошибке.
Множества базовых функций различных диалектов сильно отличаются друг от друга, и их число колеблется от нескольких десятков до нескольких сотен. Встроенные функции выполняются с большей скоростью, чем функции, определенные пользователем, так как первые реализованы на том же языке, что и вся Лисп-система (Ассемблер, С, Паскаль). Чрезмерное увеличение базового набора функций приводит к уменьшению рабочей памяти, отводимой под задачи пользователя.
2.2.4 Определение функций.
Определение функций и их вычисление в Лиспе основано на лямбда-исчислении Черча. В лямбда-исчислении Черча функция записывается в следующем виде:
lambda(x1,x2,...,xn).fn
В Лиспе лямбда-выражение имеет вид
(LAMBDA (x1 x2 ... xn) fn)
Символ LAMBDA означает, что мы имеем дело с определением функции. Символы xi являются формальными параметрами определения, которые имеют аргументы в описывающем вычисления теле функции fn. Входящий в состав формы список, образованный из параметров, называют лямбда-списком.
Телом функции является произвольная форма, значение которой может вычислить интерпретатор Лиспа.
Формальность параметров означает, что их можно заменить на любые другие символы, и это не отразится на вычислениях, определяемых функцией.
Лямбда-выражение - это определение вычислений и параметров функции в чистом виде без фактических параметров, или аргументов. Для того, чтобы применить такую функцию к некоторым аргументам, нужно в вызове функции поставить лямбда-определение на место имени функции:
(лямбда-выражение а1 а2 ... аn)
Здесь ai - формы, задающие фактические параметры, которые вычисляются как обычно.
Вычисление лямбда-вызова, или применение лямбда-выражения к фактическим параметрам, производится в два этапа. Сначала вычисляются значения фактических параметров и соответствующие формальные параметры связываются с полученными значениями. Этот этап называется связыванием параметров. На следующем этапе с учетом новых связей вычисляется форма, являющаяся телом лямбда-выражения, и полученное значение возвращается в качестве значения лямбда-вызова. Формальным параметрам после окончания вычисления возвращаются те связи, которые у них, возможно были перед вычислением лямбда-вызова.
Лямбда-вызовы можно свободно объединять между собой и другими формами. Вложенные лямбда-вызовы можно ставить как на место тела лямбда-выражения, так и на место фактических параметров.
Лямбда-выражение является как чисто абстрактным механизмом для описания и определения вычислений, так и механизмом для связывания формальных и фактических параметров на время выполнения вычислений. Лямбда-выражение - это безымянная функция, которая пропадает тотчас после вычисления значения формы. Ее трудно использовать снова, так как нельзя вызвать по имени, хотя ранее выражение было доступно как списочный объект. Однако используются и безымянные функции, например при передаче функции в качестве аргумента другой функции или при формировании функции в результате вычислений, другими словами, при синтезе программ.
Лямбда-выражение соответствует используемому в других языках определению процедуры или функции, а лямбда-вызов - вызову процедуры или функции. Записывать вызовы функций полностью с помощью лямбда-вызовов не разумно, поскольку очень скоро выражения в вызове пришлось бы повторять, хотя разные вызовы одной функции отличаются лишь в части фактических параметров. Проблема разрешима путем именования лямбда-выражений и использования в вызове лишь имени.
Дать имя и определить новую функцию можно с помощью функции DEFUN:
(DEFUN имя лямбда-список тело)
DEFUN соединяет символ с лямбда-выражением, и символ начинает представлять определенные этим лямбда-выражением вычисления. Значением этой формы является имя новой функции.
В различных диалектах Лиспа вместо DEFUN используются другие имена и формы (DEFINE, DE, CSETQ и др.).
2.2.5 Рекурсия и итерация.
Будучи языком функций, символьным языком и языком списков, Лисп является и рекурсивным языком. В программировании на Лиспе рекурсия используется для организации повторяющихся вычислений. На ней же основано разбиение проблемы на подзадачи, решение которых пытаются свести к уже решенной или решаемой в данный момент задачи.
Основная идея рекурсивного определения заключается в том, что функцию можно с помощью рекуррентных формул свести к некоторым начальным значениям, к ранее определенным функциям или к самой определяемой функции, но с более «простыми» аргументами. Вычисление такой функции заканчивается в тот момент, когда оно сводится к известным начальным значениям. Разумеется, можно организовать вычисления по рекуррентным формулам и без использования рекурсии, однако при этом встает вопрос о ясности программы и доказательстве ее эквивалентности исходным формулам. Использование рекурсии позволяет легко запрограммировать вычисление по рекуррентным формулам.
В рекурсивном описании действий имеет смысл обратить внимание на следующие обстоятельства. Во-первых, процедура содержит всегда по крайней мере одну терминальную ветвь и условие окончания. Во-вторых, когда процедура доходит до рекурсивной ветви, то функционирующий процесс приостанавливается, и новый такой же процесс запускается сначала, но уже на новом уровне. Прерванный процесс каким-нибудь образом запоминается. Он будет ждать и начнет исполняться лишь после окончания нового процесса. В свою очередь, новый процесс может приостановиться, ожидать и т. д.
Так образуется как бы стек прерванных процессов, из которых выполняется лишь последний в настоящий момент времени процесс; после окончания его работы продолжает выполняться предшествовавший ему процесс. Целиком весь процесс выполнен, когда стек снова опустеет, или, другими словами, все прерванные процессы выполнятся.
Можно говорить о рекурсии по значению, когда вызов является выражением, определяющим результат функции. Если в качестве результата функции возвращается значение некоторой другой функции и рекурсивный вызов участвует в вычислении аргументов этой функции, то будем говорить о рекурсии по аргументам. Аргументом рекурсивного вызова может быть вновь рекурсивный вызов и таких вызовов может быть много.
Для обеспечения «идеологической» совместимости с другими языками программирования, а также для повышения эффективности программ при решении некоторых частных задач в язык была введена группа функций, предоставляющих возможность организации итерационной обработки информации.
В указанной группе прежде всего выделяются так называемые отображающие или MAP-функции: MAPC, MAPCAR, MAPLIST и другие. MAP-функционалы являются функциями, которые некоторым образом отображают список (последовательность) в новую последовательность или порождают побочный эффект, связанный с этой последовательностью. Каждая из них имеет более двух аргументов, значением первого должно быть имя определенной ранее или базовой функции, или лямбда-выражение, вызываемое MAP-функцией итерационно, а остальные аргументы служат для задания аргументов на каждой итерации. Естественно, что количество аргументов в обращении к MAP-функции должно быть согласовано с предусмотренным количеством аргументов у аргумента-функции. Различие между всеми MAP-функциями состоит в правилах формирования возвращаемого значения и механизме выбора аргументов итерирующей функции на каждом шаге.
Рассмотрим основные типы MAP-функций.
MAPCAR.Значение этой функции вычисляется путем применения функции fn к последовательным элементам xi списка, являющегося вторым аргументом функции. Например в случае одного списка получается следующее выражение:
(MAPCAR fn ‘(x1 x2 ... xn))
В качестве значения функционала возвращается список, построенный из результатов вызовов функционального аргумента MAPCAR
MAPLIST.MAPLIST действует подобно MAPCAR, но действия осуществляет не над элементами списка, а над последовательными CDR этого списка.
Функционалы MAPCAR и MAPLIST используются для программирования циклов специального вида и в определении других функций, поскольку с их помощью можно сократить запись повторяющихся вычислений.
Функции MAPCAN и MAPCON являются аналогами функций MAPCAR и MAPLIST. Отличие состоит в том, что MAPCAN и MAPCON не строят, используя LIST, новый список из результатов, а объединяют списки, являющиеся результатами, в один список.
LOOP.Другим типичным представителем группы итерационных функций может служить функция LOOP, имеющая в общем случае вид (LOOP expr1 expr2 ... exprN), где в качестве аргументов могут быть использованы любые синтаксически и семантически допустимые S-выражения либо специальные конструкции.
2.2.6 Функции интерпретации выражения.
Почти во всех диалектах определены функции APPLY и FUNCALL, позволяющие интерпретировать S-выражения. Обращения к этим функциям имеют следующий вид:
(APPLY fun arg)
(FUNCALL fun arg1 arg2 ... argN)
APPLY и FUNCALL вычисляют функции, являющиеся их первыми аргументами, производя связывание формальных аргументов с указанными S-выражениями arg или arg1, arg2, ... argN. В качестве значения возвращается результат применения функции fun, которая может быть встроенной или определенной функцией или лямбда-выражением.
Необходимо отметить еще одну особенность языка Лисп, которая вытекает из природы организации структур данных и программ и механизма их интерпретации. На языке легко реализовать задачи автоматического синтеза программ. Он позволяет с помощью одних функций формировать определения других функций, программно анализировать и редактировать эти определения как S-выражения, а затем исполнять их.
2.2.7 Макросредства.
Часто бывает полезно не выписывать вычисляемое выражение вручную, а сформировать его с помощью программы. Эта идея автоматического динамического программирования особенно хорошо реализуется в Лиспе. Программное формирование выражений наиболее естественно осуществляется с помощью специальных макросов. Использование макросредств, предлагаемых современными Лисп-системами, - один из самых эффективных путей реализации сложных программ. Макросы дают возможность расширять синтаксис и семантику Лиспа и использовать новые подходящие для решаемой задачи формы предложений. Они дают возможность писать компактные, ориентированные на задачу программы, которые автоматически преобразуются в более сложный, но более близкий машине эффективный лисповский код. При наличии макросредств некоторые функции в языке могут быть определены в виде макрофункций. Такое определение фактически задает закон предварительного построения тела функции непосредственно перед фазой интерпретации.
Синтаксис определения макроса выглядит так же, как синтаксис используемой при определении функций формы DEFUN:
(DEFMACRO имя лямбда-список тело)
Вызов макроса совпадает по форме с вызовом функции, но его вычисление отличается от вычисления вызова функции. Первое отличие состоит в том, что в макросе не вычисляются аргументы. Тело макроса вычисляется с аргументами в том виде, как они записаны.
Второе отличие состоит в том, что интерпретация функций, определенных как макро, производится в два этапа. На первом, называемом макрорасширением, происходит формирование лямбда-определения функции в зависимости от текущего контекста, на втором осуществляется интерпретация созданного лямбда-выражения.
Макросы отличаются от функций и в отношении контекста вычислений. Во время расширения макроса доступны синтаксические связи из контекста определеня. Вычисление же полученной в результате расширения формы производится вне контекста макровызова, и поэтому статические связи из макроса не действуют. Использование макрофункций облегчает построение языка с лиспоподобной структурой, имеющего свой синтаксис, более удобный для пользователя. Чрезмерное использование макросредств затрудняет чтение и понимание программ.
2.2.8 Функции ввода-вывода.
Современные диалекты языка Лисп, как правило, имеют развитые средства управления вводом-выводом. Основу этих средств составляют три основные функции READ, RATOM и PRINT. Первые две позволяют осуществлять операций ввода S-выражений (READ) и атомов (RATOM), последняя выполняет вывод S-выражений.
Лисповская функция чтения READ обрабатывает выражение целиком. Вызов функции осуществляется в виде
(READ)Функция не показывает, что она ждет ввода выражения. Она лишь читает выражение и возвращает в качестве значения само это выражение, после чего вычисления продолжаются.
Для вывода выражений используют функцию PRINT. Это функция с одним аргументом, которая сначала вычисляет значение аргумента, а затем выводит это значение. Функция PRINT перед выводом аргумента переходит на новую строку, а после него выводит пробел. Таким образом, значение выводится всегда на новую строку. Более подробно эти и другие функции рассмотрим в лабораторных работах.
Базовый набор функций обычно наряду с указанными функциями включает различные их модификации и дополнительные функции, позволяющие при программировании легко получить некоторые дополнительные эффекты (автоматическое дополнение печатной строки с изображением S-выражения специальными символами перевода каретки на начало следующей строки, блокировка специальных метасимволов при выводе литеральных атомов, в печатных именах которых присутствуют непечатные символы и т. д.). кроме того, практически каждый диалект содержит набор функций управления входными и выходными потоками для связи с внешними устройствами ЭВМ. Однако указанные функции являются одной из наиболее машинно-зависимых составляющих Лисп-систем, поскольку по необходимости учитывают специфику среды операционной системы.
2.3 Знания в ИИ.
2.3.1 Требования к знаниям.
Знания должны отвечать следующим требованиям:
Должны быть явными и доступными. Это главное отличие знаний от других программных продуктов.
Использовать высококачественный опыт специалистов, т, е, знания должны отражать уровень наиболее квалифицированных специалистов в данной области.
Обладать гибкостью, т. е. система может наращиваться постепенно в соответствии с нуждами бизнеса или заказчика.
Иметь систему объяснений. Интересует не только ответ, но и как машина к нему пришла.
Обладать возможностью прогнозирования. Система должна не только давать ответы на конкретно поставленные вопросы, но и показывать как они изменяются в новой ситуации.
Память должна быть инстуциональной, т. е. специалисты уходят, их опыт остается. База знаний становится постоянно обновляющимся справочником наилучших стратегий и методов.
Похожие работы
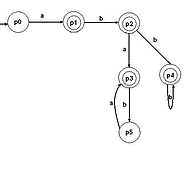
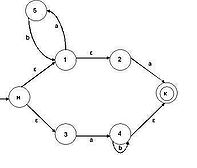
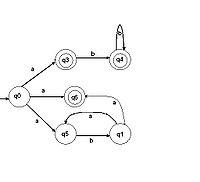
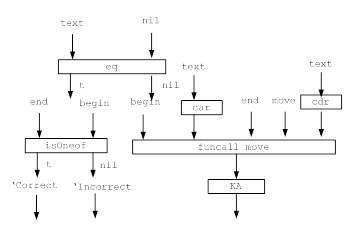
... цифр с требуемым числом разрядов и, таким образом, запомнить любое самое большое число данной разрядности. Целью данной курсовой работы является ЛИСП-реализация конечных автоматов.1. Постановка задачи Конечный автомат – автомат, проверяющий допустимость слова на ленте, и возвращающий True / False (в данном случае Correct / Incorrect). Конечный автомат может двигаться по ленте только в одном ...
... При работе пользователя с базой данных над ее содержимым выполняются следующие основные операции: выбор, добавление, модификация (замена) и удаление данных. Целью данной курсовой работы является ЛИСП – реализация основных операций над базами данных. 1 Постановка задачи Требуется разработать программу, реализующую основные операции над базами данных: выбор, добавление, модификация и удаление ...
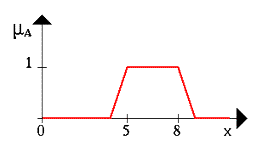
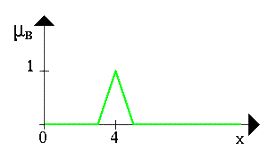
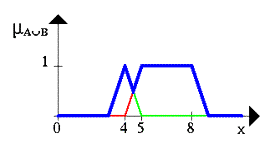
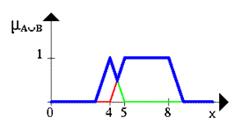
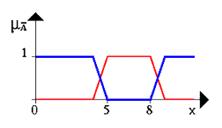
... новых рынков, биржевой игре, оценки политических рейтингов, выборе оптимальной ценовой стратегии и т.п. Появились и коммерческие системы массового применения. Целью данной курсовой работы является ЛИСП – реализация основных операций над нечеткими множествами. 1.Постановка задачи Требуется реализовать основные операции над нечеткими множествами: 1) содержание; 2) равенство; 3) ...
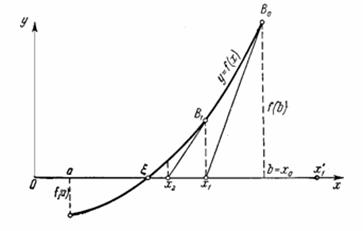
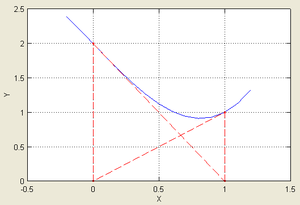
... метода Ньютона на случай мнимых корней полиномов степени выше второй и комплексных начальных приближений. Эта работа открыла путь к изучению теории фракталов. Целью данной курсовой работы является Лисп – реализация нахождения корней уравнения методом Ньютона. 1. Постановка задачи Дано уравнение: . Требуется решить это уравнение, точнее, найти один из его корней (предполагается, что ...

0 комментариев