Навигация
Применяющие функционалы
2. Применяющие функционалы.
Функции, которые позволяют вызывать другие функции, т. е. применять функциональный аргумент к его параметрам называют применяющими функционалами. Они дают возможность интерпретировать и преобразовывать данные в программу и применять ее в вычислениях.
APPLY
APPLY является функцией двух аргументов, из которых первый аргумент представляет собой функцию, которая применяется к элементам списка, составляющим второй аргумент функции APPLY:
(APPLY fn список)
_(SETQ a ‘+) р +
_(APPLY a ‘(1 2 3)) р 6
_(APPLY ‘+ ‘(4 5 6)) р 15
FUNCALL.
Функционал FUNCALL по своему действию аналогичен APPLY, но аргументы для вызываемой он принимает не списком, а по отдельности:
(FUNCALL fn x1 x2 ... xn)
_(FUNCALL ‘+ 4 5 6) р 15
FUNCALL и APPLY позволяют задавать вычисления (функцию) произвольной формой, например, как в вызове функции, или символом, значением которого является функциональный объект. Таким образом появляется возможность использовать синонимы имени функции. С другой стороны, имя функции можно использовать как обыкновенную переменную, например для хранения другой функции (имени или лямбда-выражения), и эти два смысла (значение и определение) не будут мешать друг другу:
_(SETQ list ‘+) р +
_(FUNCALL list 1 2) р 3
_(LIST 1 2) р (1 2)
3. Отображающие функционалы.
Отображающие или MAP-функционалы являются функциями, которые являются функциями, которые некоторым образом отображают список (последовательность) в новую последовательность или порождают побочный эффект, связанный с этой последовательностью. Каждая из них имеет более двух аргументов, значением первого должно быть имя определенной ранее или базовой функции, или лямбда-выражение, вызываемое MAP-функцией итерационно, а остальные аргументы служат для задания аргументов на каждой итерации. Естественно, что количество аргументов в обращении к MAP-функции должно быть согласовано с предусмотренным количеством аргументов у аргумента-функции. Различие между всеми MAP-функциями состоит в правилах формирования возвращаемого значения и механизме выбора аргументов итерирующей функции на каждом шаге.
Рассмотрим основные типы MAP-функций.
MAPCAR.Значение этой функции вычисляется путем применения функции fn к последовательным элементам xi списка, являющегося вторым аргументом функции. Например в случае одного списка получается следующее выражение:
(MAPCAR fn ‘(x1 x2 ... xn))
В качестве значения функционала возвращается список, построенный из результатов вызовов функционального аргумента MAPCAR.
_(MAPCAR ‘LISTP ‘((f) h k (i u)) р (T NIL NIL T)
_(SETQ x ‘(a b c)) р (a b c)
_(MAPCAR ‘CONS x ‘(1 2 3)) р ((a . 1) (b . 2) (c . 3))
MAPLIST.
MAPLIST действует подобно MAPCAR, но действия осуществляет не над элементами списка, а над последовательными CDR этого списка.
_(MAPLIST ‘LIST ‘((f) h k (i u)) р (T T T T)
_(MAPLIST ‘CONS ‘(a b c) ‘(1 2 3)) р (((a b c) 1 2 3) ((b c) 2 3) ((c ) 3))
Функционалы MAPCAR и MAPLIST используются для программирования циклов специального вида и в определении других функций, поскольку с их помощью можно сократить запись повторяющихся вычислений.
Функции MAPCAN и MAPCON являются аналогами функций MAPCAR и MAPLIST. Отличие состоит в том, что MAPCAN и MAPCON не строят, используя LIST, новый список из результатов, а объединяют списки, являющиеся результатами, в один список.
4. Макросы.
Программное формирование выражений наиболее естественно осуществляется с помощью макросов. Макросы дают возможность писать компактные, ориентированные на задачу программы, которые автоматически преобразуются в более сложный, но более близкий машине эффективный лисповский код. При наличии макросредств некоторые функции в языке могут быть определены в виде макрофункций. Такое определение фактически задает закон предварительного построения тела функции непосредственно перед фазой интерпретации.
Синтаксис определения макроса выглядит так же, как синтаксис используемой при определении функций формы DEFUN:
(DEFMACRO имя лямбда-список тело)
Вызов макроса совпадает по форме с вызовом функции, но его вычисление отличается от вычисления вызова функции. Первое отличие состоит в том, что в макросе не вычисляются аргументы. Тело макроса вычисляется с аргументами в том виде, как они записаны.
Второе отличие состоит в том, что интерпретация функций, определенных как макро, производится в два этапа. На первом, называемом макрорасширением, происходит формирование лямбда-определения функции в зависимости от текущего контекста, на втором осуществляется интерпретация созданного лямбда-выражения.
_(DEFMACRO setqq (x y)
(LIST ‘SETQ x (LIST ‘QUOTE y))) р setqq
_(setqq a (b c)) р (b c)
_a р (b c)
Макросы отличаются от функций и в отношении контекста вычислений. Во время расширения макроса доступны синтаксические связи из контекста определения. Вычисление же полученной в результате расширения формы производится вне контекста макровызова, и поэтому статические связи из макроса не действуют. Использование макрофункций облегчает построение языка с лиспоподобной структурой, имеющего свой синтаксис, более удобный для пользователя. Чрезмерное использование макросредств затрудняет чтение и понимание программ.
5. Задания к лабораторной работе.
1. Напишите рекурсивную функцию, определяющую сколько раз функция FIB вызывает саму себя. Очевидно, что FIB(1) и FIB(2) не вызывают функцию FIB.
2. Напишите функцию для вычисления полиномов Лежандра (P0(x)=1, P1(x)=x, Pn+1(x)= ((2*n+1)*x*Pn(x)-n*Pn-1(x))/(n+1) при n>1).
3. Напишите функцию:
вычисляющую число атомов на верхнем уровне списка (Для списка (а в ((а) с) е) оно равно трем.);
определяющую число подсписков на верхнем уровне списка;
вычисляющую полное число подсписков, входящих в данный список на любом уровне.
4. Напишите функцию:
от двух аргументов X и N, которая создает список из N раз повторенных элементов X;
удаляющую повторные вхождения элементов в список;
которая из данного списка строит список списков его элементов, например, (a b) р ((a) (b));
вычисляющую максимальный уровень вложения подсписков в списке;
единственным аргументом которой являлся бы список списков, объединяющую все эти списки в один;
зависящую от трех аргументов X, N и V, добавляющую X на N-е место в список V.
5. Напишите функцию:
аналогичную функции SUBST, но в которой третий аргумент W обязательно должен быть списком;
которая должна производить замены X на Y только на верхнем уровне W;
заменяющую Y на число, равное глубине вложения Y в W, например Y=A, W=((A B) A (C (A (A D)))) р ((2 B) 1 (C (3 (4 D))));
аналогичную функции SUBST, но производящую взаимную замену X на Y, т. е. X р Y, Y р X.
6. Вычислите значения следующих вызовов:
(APPLY ‘LIST ‘(a b));
(FUNCALL ‘LIST ‘(a b));
(FUNCALL ‘APPLY ‘LIST ‘(a b));
(FUNCALL ‘LIST ‘APPLY ‘(a b);
7. Определите функционал (A-APPLY f x), который применяет каждую функцию fi списка
f = (f1 f2 ... fn)
к соответствующему элементу xi списка
x = (x1 x2 ... xn)
и возвращает список, сформированный из результатов.
8. Определите функциональный предикат (КАЖДЫЙ пред список), который истинен в том и только в том случае, когда, являющийся функциональным аргументом предикат пред истинен для всех элементов списка список.
9. Определите функциональный предикат (НЕКОТОРЫЙ пред список), который истинен, когда предикат истинен хотя бы для одного элемента списка.
10. Определите FUNCALL через функционал APPLY.
11. Определите функционал (MAPLIST fn список) для одного списочного аргумента.
12. Определите макрос, который возвращает свой вызов.
13. Определите лисповскую форму (IF условие p q) в виде макроса.
Примеры написания функций.
;Subst - заменяет все вхождения Y в W на X.
(DEFUN subst (x y w)
(COND ((NULL w) NIL) ;проверка на окончание списка
((EQUAL ‘y ‘w) x)
((ATOM ‘w) w) ;
(t (CONS (subst x y (car w)) ;поиск в глубину
(subst x y (cdr w)))))) ;поиск в ширину
;COMPARE1 - сравнение с образцом
(defun compare1 (p d)
(cond ((and (null p) (null d)) t) ;исчерпались списки?
((or (null p) (null d)) nil) ;одинакова длина списков?
((or (equal1 (car p) '&) ;присутствует в образце атом &
(equal1 (car p) (car d))) ;или головы списков равны
(compare1 (cdr p) (cdr d))) ;& сопоставим с любым атомом
((equal1 (car p) '*) ;присутствует в образце атом *
(cond ((compare1 (cdr p) d)) ;* ни с чем не сопоставима
((compare1 (cdr p) (cdr d))) ;* сопоставима с одним атомом
((compare1 p (cdr d))))))) ;* сопоставима с несколь ;кими атомами
6. Вопросы.
1. Что такое рекурсия?
2. Назовите достоинства ее использования?
3. Что такое функционал?
4. Назовите особенности применяющих и отображающих функционалов?
5. Для чего они используются?
6. Что такое макрос?
7. Когда их используют?
Лабораторная работа №5.
Тема: Типы данных и средства работы с ними. Представление знаний.
Цель: Изучить типы данных, используемые в MuLisp, а так же научиться применять их в программах.
Точечная нотация.
Структурированные типы данных.
Представление знаний.
Задания к лабораторной работе.
Вопросы.Похожие работы
... цифр с требуемым числом разрядов и, таким образом, запомнить любое самое большое число данной разрядности. Целью данной курсовой работы является ЛИСП-реализация конечных автоматов.1. Постановка задачи Конечный автомат – автомат, проверяющий допустимость слова на ленте, и возвращающий True / False (в данном случае Correct / Incorrect). Конечный автомат может двигаться по ленте только в одном ...
... При работе пользователя с базой данных над ее содержимым выполняются следующие основные операции: выбор, добавление, модификация (замена) и удаление данных. Целью данной курсовой работы является ЛИСП – реализация основных операций над базами данных. 1 Постановка задачи Требуется разработать программу, реализующую основные операции над базами данных: выбор, добавление, модификация и удаление ...
... новых рынков, биржевой игре, оценки политических рейтингов, выборе оптимальной ценовой стратегии и т.п. Появились и коммерческие системы массового применения. Целью данной курсовой работы является ЛИСП – реализация основных операций над нечеткими множествами. 1.Постановка задачи Требуется реализовать основные операции над нечеткими множествами: 1) содержание; 2) равенство; 3) ...
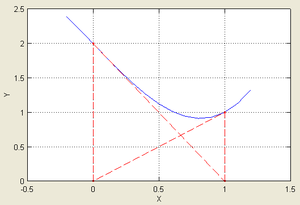
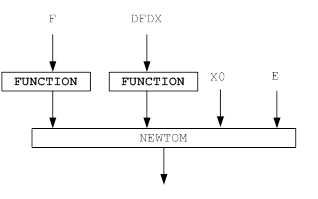
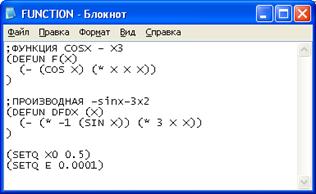
... метода Ньютона на случай мнимых корней полиномов степени выше второй и комплексных начальных приближений. Эта работа открыла путь к изучению теории фракталов. Целью данной курсовой работы является Лисп – реализация нахождения корней уравнения методом Ньютона. 1. Постановка задачи Дано уравнение: . Требуется решить это уравнение, точнее, найти один из его корней (предполагается, что ...

0 комментариев