Навигация
Последовательные вычисления
2. Последовательные вычисления.
Предложения PROG1 и PROGN позволяют работать с несколькими вычисляемыми формами:
(PROG1 форма1 ... формаN)
(PROGN форма1 ... формаN)
Эти специальные формы последовательно вычисляют свои аргументы и в качестве значения возвращают значение первого (PROG1) или последнего (PROGN) аргумента.
_(PROG1 (SETQ x 1) (SETQ y 5)) р 1
_(PROGN (SETQ j 8) (SETQ z (+x j))) р 9
3. Разветвление вычислений.
Условное предложение COND:
(COND (p1 a1)
...
(pn an))
Предикатами pi и результирующими выражениями ai могут быть произвольные формы. Выражения pi вычисляются последовательно до тех пор, пока не встретится выражение, значением которого является T. Вычисляется результирующее выражение, соответствующее этому предикату, и полученное значение возвращается в качестве значения всего предложения COND. Если истинного предиката нет то значением COND будет NIL.
Рекомендуется в качестве последнего предиката использовать символ T. Тогда соответствующее ему an будет вычисляться в том случае, если другие условия не выполняются.
Если условию не ставится в соответствие результирующее выражение, то в качестве результата выдается само значение предиката. Если же условию соответствуют несколько форм, то при его истинности формы вычисляются последовательно слева на право и результатом предложения COND будет значение последней формы.
Предложения COND можно комбинировать.
(COND ((> x 0) (SETQ рез x))
((< x 0) (SETQ x -x) (SETQ рез х))
((= х 0))
(Т ‘ошибка))
Предложение IF.
(IF условие то-форма иначе-форма)
(IF (> x 0) (SETQ y (+ y x)) (SETQ y (- y x)))
Если выполняется условие (т. е. х>0), то к значению y прибавляется значение х, иначе (x x y) (IF (< x z) (PROGN (PRINT x)
(PRINT «среднее (1)»))
(IF (> y z) (PROGN (PRINT y)
(TERPRI)
(PRINT «среднее (2)»))
(PROGN (PRIN1 z)
(PRIN1«среднее (3)»)))))
((< x y) (IF (< y z) (PROGN (PRIN1 y)
(TERPRI)
(PRIN1 «среднее (4)»))
(IF (> x z) (PROGN (PRINC x)
(PRINC «среднее (5)»))
(PROGN (PRINC z)
(TERPRI)
(PRINC «среднее (6)»)))))
(T (PRINC «ошибка ввода»))))
7. Вопросы.
1. Для чего используется предложение LET?
2. В чем его отличие от предложения LET*?
3. Чем различаются функции COND и IF?
4. Каковы возвращаемые ими значения?
5. Чем различаются функции PROG1 и PROGN?
6. Почему не желательно использовать операторы передачи управления? Чем их можно заменить?
Лабораторная работа №4.
Тема: Рекурсия в Лиспе. Функционалы и макросы.
Цель: Изучить основы программирования с применением рекурсии. Научиться работать с функционалами и макросами.
1. Рекурсия. Различные формы рекурсии.
2. Применяющие функционалы.
3. Отображающие функционалы.
4. Макросы.
5. Задание к лабораторной работе.
6. Вопросы.
1. Рекурсия. Различные формы рекурсии.
Основная идея рекурсивного определения заключается в том, что функцию можно с помощью рекуррентных формул свести к некоторым начальным значениям, к ранее определенным функциям или к самой определяемой функции, но с более «простыми» аргументами. Вычисление такой функции заканчивается в тот момент, когда оно сводится к известным начальным значениям.
Рекурсивная процедура, во-первых содержит всегда по крайней мере одну терминальную ветвь и условие окончания. Во-вторых, когда процедура доходит до рекурсивной ветви, то функционирующий процесс приостанавливается, и новый такой же процесс запускается сначала, но уже на новом уровне. Прерванный процесс каким-нибудь образом запоминается. Он будет ждать и начнет исполняться лишь после окончания нового процесса. В свою очередь, новый процесс может приостановиться, ожидать и т. д.
Будем говорить о рекурсии по значению и рекурсии по аргументам. В первом случае вызов является выражением, определяющим результат функции. Во втором - в качестве результата функции возвращается значение некоторой другой функции и рекурсивный вызов участвует в вычислении аргументов этой функции. Аргументом рекурсивного вызова может быть вновь рекурсивный вызов и таких вызовов может быть много.
Рассмотрим следующие формы рекурсии:
простая рекурсия;
параллельная рекурсия;
взаимная рекурсия.
Рекурсия называется простой, если вызов функции встречается в некоторой ветви лишь один раз. Простой рекурсии в процедурном программировании соответствует обыкновенный цикл.
Для примера напишем функцию вычисления чисел Фибоначчи (F(1)=1; F(2)=1; F(n)=F(n-1)+F(n-2) при n>2):
(DEFUN FIB (N)
(IF (> N 0)
(IF (OR N=1 N=2) 1
(+ (FIB (- N 1)) (FIB (- N 2))))
‘ОШИБКА_ВВОДА))
Рекурсию называют параллельной, если она встречается одновременно в нескольких аргументах функции:
(DEFUN f ...
...(g ... (f ...) (f ...) ...)
...)
Рассмотрим использование параллельной рекурсии на примере преобразования списочной структуры в одноуровневый список:
(DEFUN PREOBR (L)
(COND
((NULL L) NIL)
((ATOM L) (CONS (CAR L) NIL))
(T (APPEND
(PREOBR (CAR L))
(PREOBR (CDR L))))))
Рекурсия является взаимной между двумя и более функциями, если они вызывают друг друга:
(DEFUN f ...
...(g ...) ...)
(DEFUN g ...
...(f ...) ...)
Для примера напишем функцию обращения или зеркального отражения в виде двух взаимно рекурсивных функций следующим образом:
(DEFUN obr (l)
(COND ((ATOM l) l)
(T (per l nil))))
(DEFUN per (l res)
(COND ((NULL l) res)
(T (per (CDR l)
(CONS (obr (CAR l)) res)))))
Похожие работы
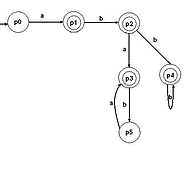
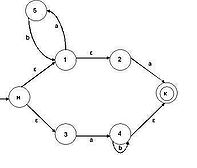
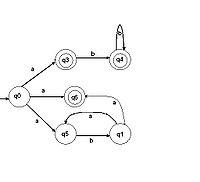
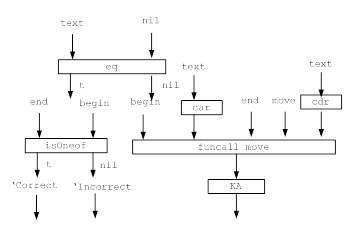
... цифр с требуемым числом разрядов и, таким образом, запомнить любое самое большое число данной разрядности. Целью данной курсовой работы является ЛИСП-реализация конечных автоматов.1. Постановка задачи Конечный автомат – автомат, проверяющий допустимость слова на ленте, и возвращающий True / False (в данном случае Correct / Incorrect). Конечный автомат может двигаться по ленте только в одном ...
... При работе пользователя с базой данных над ее содержимым выполняются следующие основные операции: выбор, добавление, модификация (замена) и удаление данных. Целью данной курсовой работы является ЛИСП – реализация основных операций над базами данных. 1 Постановка задачи Требуется разработать программу, реализующую основные операции над базами данных: выбор, добавление, модификация и удаление ...
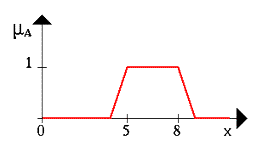
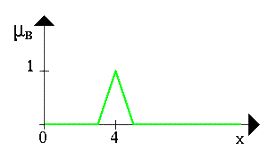
... новых рынков, биржевой игре, оценки политических рейтингов, выборе оптимальной ценовой стратегии и т.п. Появились и коммерческие системы массового применения. Целью данной курсовой работы является ЛИСП – реализация основных операций над нечеткими множествами. 1.Постановка задачи Требуется реализовать основные операции над нечеткими множествами: 1) содержание; 2) равенство; 3) ...
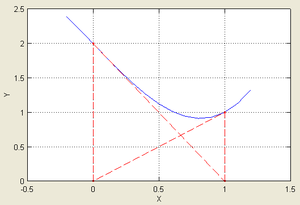
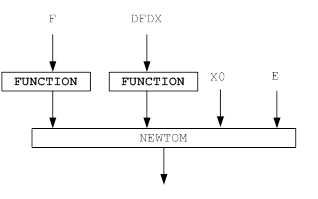
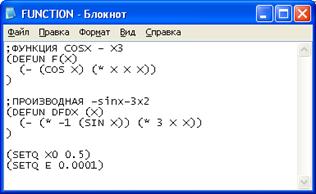
... метода Ньютона на случай мнимых корней полиномов степени выше второй и комплексных начальных приближений. Эта работа открыла путь к изучению теории фракталов. Целью данной курсовой работы является Лисп – реализация нахождения корней уравнения методом Ньютона. 1. Постановка задачи Дано уравнение: . Требуется решить это уравнение, точнее, найти один из его корней (предполагается, что ...

0 комментариев