Группы геометрических преобразований. Группы вращений, подобий, гомотетий с заданным общим центром, параллельных переносов
Арифметические функции: t(n), s(n), j(n)
Алгоритм Евклида и его применения
Линейное представление наибольшего общего делителя
Базис пространства решений однородной системы линейных уравнений - это фундаментальная система решений
Корни многочлена; схема Горнера; теорема Безу
Разложение многочлена в произведение неприводимых
Теорема о строении простого алгебраического расширения
Навигация
Базис пространства решений однородной системы линейных уравнений - это фундаментальная система решений
Программа государственного экзамена по математике для студентов математического факультета Московского городского педагогического университета
38950
знаков
13
таблиц
4
изображения
2. Базис пространства решений однородной системы линейных уравнений - это фундаментальная система решений.
3. Пространство матриц 
имеет стандартный базис из матричных единиц Eij (единица находится на месте с номером (i, j), следовательно,
dim = nm.
4. Пространства многочленов Qn[x] с рациональными коэффициентами степени не превосходящей n имеет следующие базисы:
а) стандартный базис вида 1, x, x2, . . . , xn;
б) базис Тейлора “в точке c”:
1, (x - c), (x - c)2, . . . , (x - c)n , где c - некоторое число;
в) [базис Лагранжа “в точке (c1, . . . , cn+1)”:
gi(x) = {(x - c1) . . . (x - ci)^ . . . (x - cn+1)}/ {(ci - c1) . . . (ci - ci)^ . . . (ci - cn+1)},
где c1, . . . , cn+1 - попарно различные скаляры, а знак ^ означает отсутствие указанного множителя.]
Координаты многочлена f(x)
относительно стандартного базиса - это его коэффициенты;
относительно базиса Тейлора - это строка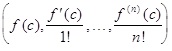 
;
[относительно базиса Лагранжа - это строка (f(c1), . . . , f(cn+1)).]
5. Вещественное линейное пространство C имеет стандартный базис (1, i).
7. Основные теоремы о системах линейных уравнений
10. Исследование системы линейных уравнений.
Пусть задана система линейных уравнений: Ax = b, где A- основная матрица, x- столбец переменных, b - столбец свободных членов. С помощью элементарных преобразований строк в основной матрице можно построить максимальную систему единичных столбцов. Кроме того, удалим из расширенной матрицы нулевые строки. Тогда можно считать, что расширенная матрица системы уравнений имеет вид:
,
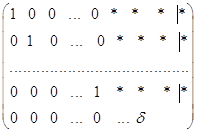где в последней строке ведущий элемент обозначен через d.
Для ненулевого числа d возможны два случая:
(а) d находится до черты, т.е. лежит в основной матрице. Следовательно, в этом случае мы можем написать общее решение совместной системы. Заметим, что все переменные будут связаны Û ранг основной матрицы равен числу переменных системы.
(б) d находится после черты; тогда система несовместна и ранг основной матрицы меньше ранга расширенной матрицы на единицу.
Тем самым, мы доказали теорему.
Теорема. Пусть d - ведущий элемент последней строки приведенной ступенчатой матрицы. Тогда
(а) система совместна Û d находится до черты;
(б) система несовместна Û d находится после черты;
(в) система является определенной Û d находится до черты и все переменные связанные;
(г) система является неопределенной Û d находится до черты и имеется хотя бы одна свободная переменная.
20. Критерии совместности и определенности.
Из приведенной теоремы немедленно вытекают следующие два критерия.
Критерий совместности (теорема Кронеккера-Капелли). Система Ax = b линейных уравнений является совместной Û ранг основной матрицы равен рангу расширенной матрицы, т.е. r(A) = r(A½b).
Критерий определенности. Система Ax = b линейных уравнений от n переменных является определенной Û ранг основной матрицы равен рангу расширенной матрицы и равен числу переменных в системе, т.е. r(A) = r(A½b) = n.
30. Связь между решениями совместной неоднородной и связанной с ней однородной системами линейных уравнений.
Допустим, что дана совместная система линейных уравнений:
| Ax = b. | (1) |
Пусть z0, z1, z2 - частные решения системы (1), z - ее общее решение. Тогда справедливы равенства Az1t = b, Az2t = b. Вычитая почленно из первого второе, на основании известных свойств, получаем: 0 = Az1t - Az2t = A(z1t - z2t) = A(z1 - z2)t, т.е. разность между двумя частными решения системы (1) является решением связанной с ней однородной системы
| Ax = 0. | (2) |
Если теперь x - общее решение системы (2), то имеем Ax t = 0, следовательно,
b = b + 0 = Az0t + Ax t = A(z0t +x t) = A(z0 +x )t,
т.е. сумма частного решения системы (1) и общего решения системы (2) является решением системы (1).
Таким образом, справедлива
Теорема. Общее решение совместной неоднородной системы (1) является суммой частного решения системы (1) и общего решения системы (2).
Поскольку общее решение однородной системы может быть записано в виде линейной комбинации ФСР, то получаем, что общее решение системы (1) можно записать в следующей параметрической форме:
z = z0 + a1x1 + a2x2 + . . . + amxm,
где z0 - какое-нибудь частное решение системы (1); x1, x2, . . . , xm - ФСР системы (2),
a1, a2, . . . , am - действительные параметры; m = n - r(A).
Похожие работы
... учебного процесса методической подготовки будущего учителя. Основное содержание исследования отражено в следующих публикациях автора: I. Монографии: 1. Абдуразаков М.М. Совершенствования содержания подготовки будущего учителя информатики в условиях информатизации образования. –Махачкала: ДГПУ, 2006. –190 с. 12 п.л. 2. Гаджиев Г.М., Абдуразаков М.М. Технология преподавания информатики. – ...
... профиля и специализации. На факультетах общественных наук предметы, входившие в минимум, изучались в расширенном объеме[4]. 2. Положение русского студенчества в конце XIX начале XX века 2.1 Образ русского студента в конце XIX начале XX века В отличие от закрытых учебных заведений, в которых учились в основном дворяне, значительное число учащихся в университетах были людьми незнатными ...
... и устойчивых требований, которые определяют характер и особенности организации коррекционно-образовательного процесса и управления познавательной деятельностью лиц с особыми образовательными потребностями. Специальная педагогика опирается на соответствующие обще- педагогические принципы организации образования и управления познавательной деятельностью, однако их реализация в системе специального ...
... покровителей, сделавших особый вклад в развитие культуры, в Европе называют медичи. Конец девятнадцатого века в России был ознаменован необычайным подъёмом культуры. В связи с этим появились в стране и те, кто этот подъём всячески поддерживал, в том числе и материально. Эти люди были в основном богатыми купцами и промышленниками, которые чувствовали необычайный прогресс в развитии культуры ...
0 комментариев