Навигация
Разбиение области в фазовой плоскости на траектории
5. Разбиение области в фазовой плоскости на траектории
Некоторые элементарные сведения о траекториях.
Лемма 6. Всяким двум решениям, отличающимся только выбором начального значения t0, соответствует одна и та же траектория.
В другой терминологии — «положением равновесия» или «точкой покоя».
Доказательство. В силу лемм 1 и 2 всякие два решения, отличающиеся выбором начальных значений t0 (но имеющие одни и те же Начальные значения ![]() ), могут быть получены одно из другого заменой t на t + С. Но если даны два решении
), могут быть получены одно из другого заменой t на t + С. Но если даны два решении
![]() (15)
(15)
![]() (16)
(16)
причем решение (15) определено на интервале (![]() , Т), а решение (16) — на интервале (
, Т), а решение (16) — на интервале (![]() — С, Т — С), то, очевидно, им соответствует одна и та же траектория (так как замена в (15) t через t +С является просто заменой обозначении переменного). Лемма доказана.
— С, Т — С), то, очевидно, им соответствует одна и та же траектория (так как замена в (15) t через t +С является просто заменой обозначении переменного). Лемма доказана.
Теорема 3. Через каждую точку области G проходит одна и только одна траектория динамической системы (1).
Доказательство. Пусть М0 (х0, у0) — произвольная точка области G.
Тогда в силу теоремы 1 (о существовании и единственности решения) при всяком t существует решение, соответствующее начальным значениям t0, x0, ![]()
![]()
Это, очевидно, и означает, что через точку х0, у0 проходит хотя бы одна траектория L.
Предположим теперь, что через одну и ту же точку М0 (х0, у0) области G проходят две различные траектории L и L*.
Пусть
![]()
— решение, соответствующее траектории L*. Это решение, очевидно, непременно должно быть таким, чтобы при некотором значении t = t* мы имели бы
![]()
но тогда в силу леммы 2 при надлежащем выборе С мы должны иметь
![]()
и, следовательно (см. лемму 6), траектории L и L* вопреки предположению не могут быть различны. Теорема доказана.
Замечание 1. Из проведенного в теореме рассуждения непосредственно вытекает, что всякие два различных решения, соответствующих одной и той же траектории, получаются друг из друга заменой t на t +С, т. е. отличаются друг от друга только выбором начального значения t0 (см. лемму 2).
Замечание 2. Пусть при каком-либо выборе решения, соответствующего траектории L, точке М0 этой траектории соответствует значение t0, а точке M1 — значение t0 +![]() . Тогда из замечания 1 следует, что если при некотором другом выборе решения, соответствующего траектории L, точке М0 соответствует значение t*, то значению t* +
. Тогда из замечания 1 следует, что если при некотором другом выборе решения, соответствующего траектории L, точке М0 соответствует значение t*, то значению t* +![]() соответствует точка
соответствует точка ![]() .
.
Замечание 3. Если траектория целиком лежит в ограниченной замкнутой области ![]() с G, то в силу теоремы 2 соответствующее ей решение определено при всех значениях
с G, то в силу теоремы 2 соответствующее ей решение определено при всех значениях
t (![]() < t <
< t <![]() )
)
В силу теоремы 3 динамическая система, заданная в области G, определяет некоторое семейство траекторий или, как мы будем говорить, некоторое разбиение области G на траектории.
Мы укажем здесь некоторые основные свойства траекторий. Выше мы уже останавливались на одном частном типе траекторий, именно, на состояниях равновесия.
Как мы видели, х = а, y=b тогда и только тогда является состоянием равновесия, когда выполняются условия Р(а, b) = Q(a, b) = 0.
Предположим теперь, что траектория L, соответствующая решению
![]()
не является состоянием равновесия. Во всех точках такой траектории, очевидно, выполняется неравенство
![]()
Действительно, если бы в какой-нибудь точке М*(х*, у*) траектории L, соответствующей значению t*, имело место равенство
![]()
т. е. одновременно
![]()
и это, очевидно, означало бы, что точка х*, у* является состоянием равновесия. Но состояние равновесия само является отдельной траекторией, и в силу теоремы 3 точка М* (х*, у*) не может принадлежать отличной от состояния равновесия траектории L.
Рассмотрим вопрос о том, могут ли быть у траектории, отличной от состояния равновесия, «самопересечения», т. е. возможно ли, чтобы существовали значения t1 и t2, t1![]() t2 такие, чтобы соответствующие им точки траектории совпадали.
t2 такие, чтобы соответствующие им точки траектории совпадали.
Ответ на этот вопрос дается следующей леммой:
Лемма 7. Пусть траектория L, соответствующая решению
![]() (
(![]() < t < T), (17)
< t < T), (17)
отлична от состояния равновесия, и пусть существуют значения t, t1 и t2 (![]() < t1 < t2 < T) такие, что
< t1 < t2 < T) такие, что
![]()
Тогда решение (17) определено при всех значениях
t (т. е. ![]() )
)
функции ![]() ,
, ![]() являются периодическими функциями t, а соответствующая траектория—простой гладкой замкнутой кривой.
являются периодическими функциями t, а соответствующая траектория—простой гладкой замкнутой кривой.
Доказательство. Пусть
![]() (18)
(18)
Рассмотрим наряду с решением (17) решение
![]() (19)
(19)
определенное на интервале
(![]() — С, Т — С)
— С, Т — С)
где С = t2 — t1 (см. лемму 1).
Из равенств (18) следует, что решения (17) и (19) удовлетворяют одним и тем же начальным условиям (при t = t1 , x = х0 , у =у0). Но тогда эти решения совпадают, а следовательно, совпадают интервалы значений t, на которых они определены. Но интервалы (![]() , Т) и (
, Т) и (![]() — С, Т — С) при С
— С, Т — С) при С![]() 0 могут совпадать лишь в том случае, когда
0 могут совпадать лишь в том случае, когда ![]() =-
=-![]() , Т =+
, Т =+![]() .
.
Таким образом, мы показали, что решения (17) и (19) определены для всех t (![]() < t <
< t < ![]() ). Далее, из совпадения решений (17) и (19) следует, что при всех t (—
). Далее, из совпадения решений (17) и (19) следует, что при всех t (—![]() < t <
< t < ![]() )
)
![]() (20)
(20)
где C = t2— t1 >0. Это, очевидно, означает, что функции ![]() (t) и
(t) и ![]() (t)— периодические функции с общим периодом 0 = t2 — t1. Пусть
(t)— периодические функции с общим периодом 0 = t2 — t1. Пусть
![]() ) (21)
) (21)
— наименьшее положительное число, при котором имеют место равенства
![]() (22)
(22)
Такое число непременно существует. Действительно, в противном случае можно было бы указать последовательность положительных чисел {![]() } таких, что
} таких, что
![]() и
и ![]()
Очевидно, тогда при любом n и любом целом |k|
![]()
или, зафиксировав какое-нибудь t0, можно написать
![]()
Таким образом, каждая из функции ![]() (t) и
(t) и ![]() (t) принимает одно и то же значение, равное соответственно
(t) принимает одно и то же значение, равное соответственно ![]() (
(![]() ) и
) и ![]() (
(![]() ) при всех следующих значениях t
) при всех следующих значениях t
![]()
где N может быть любым целым числом, а ![]() сколь угодно мало при достаточно большом n. Следовательно, какое бы значение t* мы ни взяли, либо t* =t
сколь угодно мало при достаточно большом n. Следовательно, какое бы значение t* мы ни взяли, либо t* =t![]() и тогда
и тогда ![]() , либо t* попадает в некоторый интервал (t0+(k-1)
, либо t* попадает в некоторый интервал (t0+(k-1)![]() , t0 +
, t0 +![]()
![]() ) или
) или
(t0—(k-1)![]() , t0 --
, t0 --![]()
![]() ) и в силу того, что Qn сколь угодно мало при достаточно большом n, существуют сколь угодно близкие к t* значения t', при которых
) и в силу того, что Qn сколь угодно мало при достаточно большом n, существуют сколь угодно близкие к t* значения t', при которых
![]()
Но тогда в силу непрерывности функций ![]() (t),
(t), ![]() (t) мы, очевидно, также имеем
(t) мы, очевидно, также имеем
![]()
Это означает, что функции ![]() (t),
(t), ![]() (t)— постоянные, т. е. траектория L состояние равновесия, что противоречит условию теоремы.
(t)— постоянные, т. е. траектория L состояние равновесия, что противоречит условию теоремы.
Очевидно, все точки траектории L могут быть получены при изменении t в уравнениях (17) от t0 до t0 + ![]() 0 (t0
0 (t0![]() t
t ![]() t0 -
t0 -![]() 0), где t0 — любое фиксированное число. Так как по самому определению
0), где t0 — любое фиксированное число. Так как по самому определению ![]() 0 есть наименьшее число,при котором выполняются равенства(22),то всяким двум значениям
0 есть наименьшее число,при котором выполняются равенства(22),то всяким двум значениям ![]() и t", t0
и t", t0![]() заведомо соответствуют различные точки траектории L. Это и означает, что траектория L является простой замкнутой кривой. В силу леммы 5 эта замкнутая кривая, очевидно, гладкая. Таким образом, лемма доказана.
заведомо соответствуют различные точки траектории L. Это и означает, что траектория L является простой замкнутой кривой. В силу леммы 5 эта замкнутая кривая, очевидно, гладкая. Таким образом, лемма доказана.
Решение, в котором функции ![]() (t) и
(t) и ![]() (t) — периодические функции t, называется периодическим решением. Наименьшее число
(t) — периодические функции t, называется периодическим решением. Наименьшее число ![]() 0 > 0, при котором выполняются равенства (22),— периодом этого решения.
0 > 0, при котором выполняются равенства (22),— периодом этого решения.
Траектория L, соответствующая периодическому решению, называется замкнутой траекторией. Очевидно, все решения, соответствующие данной замкнутой траектории, являются периодическими решениями с одним и тем же периодом. Всякая траектория, не являющаяся замкнутой траекторий или состоянием равновесия, называется незамкнутой траекторией.
Из леммы 7 следует, что у траекторий системы (I) не может быть «самопересечений», т. е. что всякая часть незамкнутой траектории, соответствующая значениям t в любом конечном сегменте, является простой гладкой дугой.
Таким образом, мы получили следующие основные элементарные сведения о траекториях. Траектория может быть: 1) состоянием равновесия, 2) замкнутой траекторией, 3) незамкнутой (несамопересекающейся) траекторией. Эти сведения являются предварительными, так как возможный характер незамкнутых траекторий остается невыясненным.
6. Сопоставление геометрической интерпретации в пространстве R3 и геометрической интерпретации на фазовой плоскости
Как мы уже указывали, каждому решению системы (I) соответствует в ![]() интегральная кривая.
интегральная кривая.
Траектория, очевидно, является проекцией этой интегральной кривой на плоскость (x, у). Из леммы 4 следует, что в траекторию проектируются те и только те интегральные кривые пространства ![]() , которые получаются из одной такой кривой (и, следовательно, друг из друга) сдвигом на произвольный отрезок вдоль оси t. Таким образом, устанавливается естественное соответствие между траекториями динамической системы на фазовой плоскости и интегральными кривыми в пространстве
, которые получаются из одной такой кривой (и, следовательно, друг из друга) сдвигом на произвольный отрезок вдоль оси t. Таким образом, устанавливается естественное соответствие между траекториями динамической системы на фазовой плоскости и интегральными кривыми в пространстве ![]() . При этом могут представиться следующие случаи в зависимости от характера траектории L:
. При этом могут представиться следующие случаи в зависимости от характера траектории L:
L есть состояние равновесия М (а, Ь). Соответствующая интегральная кривая в ![]() является прямой х = а, у = b, параллельной оси t и проходящей через точку М. При сдвиге вдоль оси t эта прямая переходит сама в себя.
является прямой х = а, у = b, параллельной оси t и проходящей через точку М. При сдвиге вдоль оси t эта прямая переходит сама в себя.
2) L есть замкнутая траектория, соответствующая решению с периодом ![]() 0. Соответствующие интегральные кривые имеют характер «винтовых линий» с шагом
0. Соответствующие интегральные кривые имеют характер «винтовых линий» с шагом ![]() 0 и проектируются в траекторию L. При сдвиге вдоль оси t на отрезок С каждая интегральная кривая переходит в другую кривую, если С не кратно
0 и проектируются в траекторию L. При сдвиге вдоль оси t на отрезок С каждая интегральная кривая переходит в другую кривую, если С не кратно ![]() 0, и сама в себя, если С кратно
0, и сама в себя, если С кратно ![]() 0 (рис. 3).
0 (рис. 3).
3) L — незамкнутая траектория. Каждая интегральная кривая, соответствующая траектории L, при любом сдвиге вдоль оси t, отличном от нулевого, переходит в другую интегральную кривую (рис. 4).
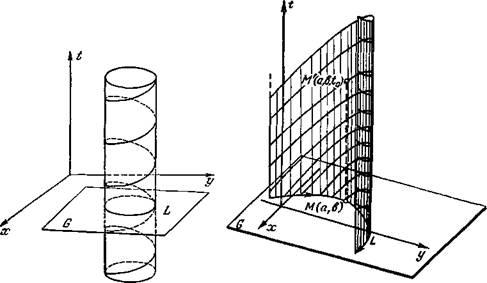
Рис. 3. Рис. 4.
Подчеркнем следующие элементарные факты. Точка, двигаясь по траектории, отличной от состояния равновесия (т. е. «изображающая точка» с координатами х = ![]() (t), y=
(t), y= ![]() (t) ), не может стремиться к точке какой-либо отличной от нее траектории при t, стремящемся к конечному значению. Действительно, в противном случае , интегральные кривые в пространстве (x, у, t) пересекались бы, что невозможно в силу теоремы 1. В частности, точка, двигаясь по траектории, отличной от состояния равновесия, может стремиться к состоянию равновесия либо при t
(t) ), не может стремиться к точке какой-либо отличной от нее траектории при t, стремящемся к конечному значению. Действительно, в противном случае , интегральные кривые в пространстве (x, у, t) пересекались бы, что невозможно в силу теоремы 1. В частности, точка, двигаясь по траектории, отличной от состояния равновесия, может стремиться к состоянию равновесия либо при t![]()
![]() , либо при
, либо при ![]()
Похожие работы
... для реализации системы бюджетирования Консультационной группы "Воронов и Максимов". Статья о проблемах выбора системы бюджетирования - в проекте "УПРАВЛЕНИЕ 3000". Бюджетный автомат Если вы решитесь на автоматизацию системы бюджетирования компании, перед вами сразу встанут вопросы: что выбрать, сколько платить, как внедрять. Примеряйте! О ЧЕМ РЕЧЬ В “Капитале” на стр. 44, 45 мы рассказали ...
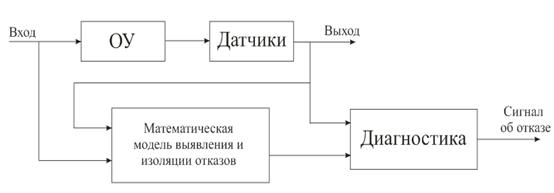
... сети могут быть использованы как классификаторы для разделения образцов рассогласований и формирования сигналов тревог. Таким образом, они могут выявлять и изолировать отказы. 3. Диагностика отказов системы регулирования уровня жидкости в баке 3.1. Постановка задачи Реализацию описанного выше метода диагностики отказов, основанного на моделях будем выполнять применительно к системе ...
... их интеграция, расширение их возможностей в новых версиях, создание новых средств и перенос их на другие аппаратные платформы и в другие ОС IBM. 12.4 Операционная система z/VM ОС z/VM [21, 24, 42] (последняя версия - V4R2) является высокопроизводительной многопользовательской интерактивной ОС, предоставляющей уникальные возможности в части выполнения различных операционных сред на одном ...
... , может приводить к большим потерям рабочего тела и раскрутке космического аппарата до недопустимых угловых скоростей. Таким образом разработка алгоритмов контроля и диагностики системы управления ориентацией космического аппарата – является актуальной задачей. В настоящей работе решается задача построения алгоритмов контроля и идентификации отказов командных приборов и исполнительных органов. ...



0 комментариев