Навигация
Динамические системы в плоской области
ТЕМА
ДИНАМИЧЕСКИЕ СИСТЕМЫ В ПЛОСКОЙ ОБЛАСТИ
1. Введение
Мы будем рассматривать системы дифференциальных уравнений вида
![]() (I)
(I)
где Р (х, у) и Q (х, у) — непрерывные функции, определенные в некоторой области G евклидовой плоскости (х, у — декартовы координаты) и имеющие в этой области непрерывные частные производные до порядка не ниже первого. Область может быть как ограниченной, так и неограниченной. В частности, область G может совпадать со всей плоскостью (х, у).
Системы вида (I) являются частным случаем систем двух дифференциальных уравнений с двумя неизвестными функциями: независимое переменное t в их правые части явно не входит. Системы дифференциальных уравнений, правые части которых не содержат явно независимое переменное, называются автономными. Автономные системы дифференциальных уравнений называются также динамическими системами.
Систему (I) мы будем называть динамической системой на плоскости или в плоской области. Мы будем также говорить, что динамическая система задана или определена в области G. В дальнейшем мы будем опускать слова «на плоскости» и «в плоской области».
Динамическая система (I), заданная в области G, называется системой класса Сn, если функции Р (х, у) и Q (я, у) являются функциями класса Сn, т. е. имеют в области G непрерывные частные производные до порядка n включительно.
Динамическая система (I) называется системой аналитического класса или аналитической системой, если функции Р и Q являются аналитическими функциями в области G.
Очевидно, всякая система класса Ck (к > 1) является одновременно системой класса Ck1, где к1 < к, в частности, системой класса C1. Аналитическая система является системой класса Ck для любого натурального к.
Все рассматриваемые в этой книге динамические системы являются системами класса ![]() . Поэтому всюду в дальнейшем под динамической системой мы будем во всяком случае всегда подразумевать систему класса
. Поэтому всюду в дальнейшем под динамической системой мы будем во всяком случае всегда подразумевать систему класса ![]() , не оговаривая этого явно.
, не оговаривая этого явно.
Изложим простейшие свойства динамических систем в плоской области. Свойства эти характерны для автономных систем дифференциальных уравнений. Неавтономные системы (т. е. системы, в правые части которых t входит явно), вообще говоря, ими не обладают .
2. Геометрическая интерпретация динамической системы (I) в пространстве -R3
Рассмотрим обычную для системы двух дифференциальных уравнений с двумя неизвестными функциями геометрическую интерпретацию, т. е. геометрическую интерпретацию в трехмерном пространстве с декартовыми координатами х, у, t.
Функции Р (х, у) и Q (х, у) нужно при этом рассматривать как функции трех переменных х, у и t. Но так как эти функции от t не зависят, то в трехмерном пространстве R3 областью определения правых частей системы (I) является бесконечная цилиндрическая область Н, образованная всеми прямыми, параллельными оси t, пересекающими плоскость (х, у) в точках области G .
Решения
![]()
системы (I) интерпретируются как кривые, расположенные в области Н. Эти кривые называются интегральными кривыми системы (I). Мы будем, здесь и всюду в дальнейшем, под решением системы дифференциальных уравнений подразумевать решение, продолженное на максимальный возможный интервал значений t.
Так как функции Р (х, у) и Q (х, у) во всяком случае являются функциями класса С1 то для системы (I) во всех точках области H выполняются условия теоремы существования и единственности, а следовательно и сама эта теорема. Мы сформулируем ее для системы (I) следующим образом:
Теорема 1. Для любой точки М0(х0,![]() )
)![]() G и для любого t0,
G и для любого t0, ![]() , существует одно и только одно решение
, существует одно и только одно решение
![]()
системы (I), удовлетворяющее начальным условиям
![]()
определенное для всех значений t в некотором определенном интервале (![]() , Т), содержащем t0.(В частности, решение может быть определено при всех значениях t, т. е. t может быть равно
, Т), содержащем t0.(В частности, решение может быть определено при всех значениях t, т. е. t может быть равно ![]() , а Т может быть равно
, а Т может быть равно ![]() ).
).
Геометрически теорема 1 означает, что через каждую точку области Н проходит интегральная кривая системы (I) и при этом только одна.
Для системы вида (I) справедлива также следующая теорема, которая существенно используется в дальнейшем:
Теорема 2. Пусть ![]() — замкнутая ограниченная область, содержащаяся в области G (
— замкнутая ограниченная область, содержащаяся в области G (![]()
![]() G),
G),
![]() (1)
(1)
— решение системы (I), определенное в интервале (![]() , Т) и такое, что при всех t на интервале (
, Т) и такое, что при всех t на интервале (![]() , Т) точка N (
, Т) точка N (![]() ,
,![]() ) все время остается в области
) все время остается в области ![]() . Тогда
. Тогда ![]() =
=![]() , T=+
, T=+![]() , т.е.решение (1) определено для всех значений t.
, т.е.решение (1) определено для всех значений t.
Доказательство. Предположим, что решение
![]()
определено при значении t - t0. Пусть ![]() — два произвольных числа, причем
— два произвольных числа, причем ![]() < t0,
< t0, ![]() > t0. Обозначим через
> t0. Обозначим через ![]() конечную цилиндрическую область пространства
конечную цилиндрическую область пространства ![]() , состоящую из всех точек М (t, x, у) таких, что
, состоящую из всех точек М (t, x, у) таких, что ![]() , а х, у таковы, что точка (х, у)
, а х, у таковы, что точка (х, у) ![]()
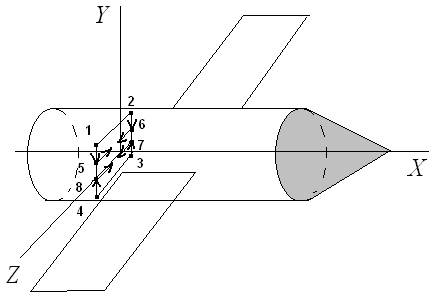
![]() (рис. 1). Интегральная кривая, соответствующая решению (1), проходит через точку М0 (t0,
(рис. 1). Интегральная кривая, соответствующая решению (1), проходит через точку М0 (t0,![]() ,
,![]() ), принадлежащую области H1. Но тогда, в силу теоремы (А') дополнения, эта интегральная кривая выходит из области
), принадлежащую области H1. Но тогда, в силу теоремы (А') дополнения, эта интегральная кривая выходит из области ![]() как при значении, большем t0, так и при значении, меньшем t0. Однако выйти из цилиндрической области
как при значении, большем t0, так и при значении, меньшем t0. Однако выйти из цилиндрической области ![]() через боковую поверхность этой области интегральная кривая не может, так как в этом случае, очевидно, нашлась бы точка N (
через боковую поверхность этой области интегральная кривая не может, так как в этом случае, очевидно, нашлась бы точка N (![]() ), лежащая вне замкнутой области
), лежащая вне замкнутой области ![]() , что противоречит условию теоремы.
, что противоречит условию теоремы.
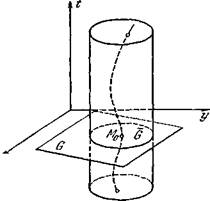
Рис. 1.
Следовательно, рассматриваемая интегральная кривая выходит из ![]() через нижнее и верхнее основания (рис. 1). Но это значит, что решение (1) определено при t =
через нижнее и верхнее основания (рис. 1). Но это значит, что решение (1) определено при t = ![]() и t =
и t =![]() . Так как
. Так как ![]() произвольны, то решение (1) определено при всех значениях t. Теорема доказана.
произвольны, то решение (1) определено при всех значениях t. Теорема доказана.
Похожие работы
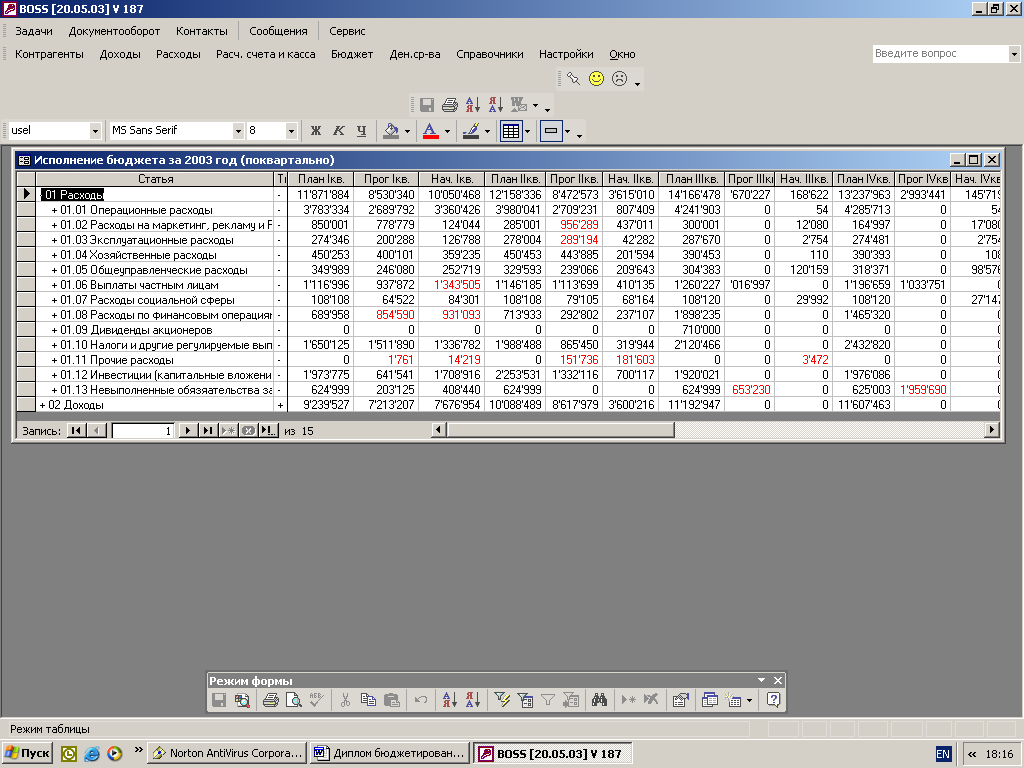
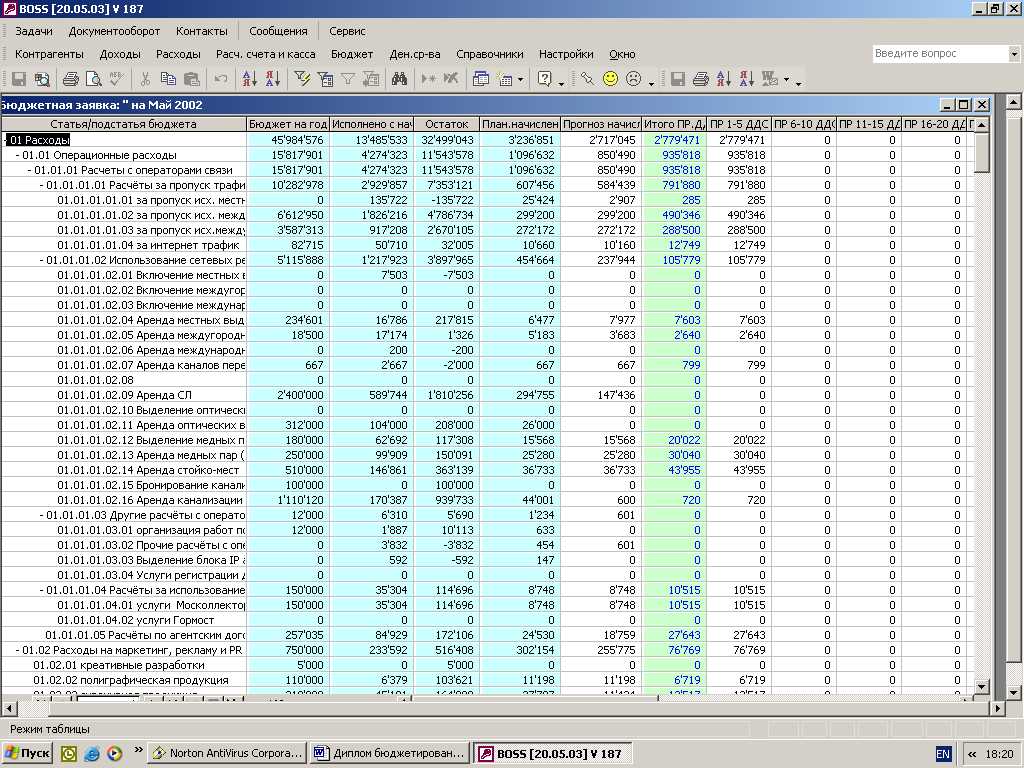
... для реализации системы бюджетирования Консультационной группы "Воронов и Максимов". Статья о проблемах выбора системы бюджетирования - в проекте "УПРАВЛЕНИЕ 3000". Бюджетный автомат Если вы решитесь на автоматизацию системы бюджетирования компании, перед вами сразу встанут вопросы: что выбрать, сколько платить, как внедрять. Примеряйте! О ЧЕМ РЕЧЬ В “Капитале” на стр. 44, 45 мы рассказали ...
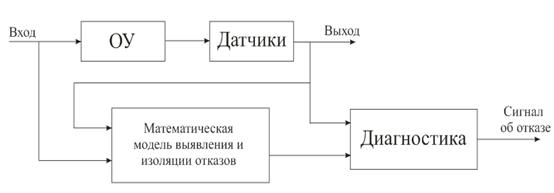
... сети могут быть использованы как классификаторы для разделения образцов рассогласований и формирования сигналов тревог. Таким образом, они могут выявлять и изолировать отказы. 3. Диагностика отказов системы регулирования уровня жидкости в баке 3.1. Постановка задачи Реализацию описанного выше метода диагностики отказов, основанного на моделях будем выполнять применительно к системе ...
... их интеграция, расширение их возможностей в новых версиях, создание новых средств и перенос их на другие аппаратные платформы и в другие ОС IBM. 12.4 Операционная система z/VM ОС z/VM [21, 24, 42] (последняя версия - V4R2) является высокопроизводительной многопользовательской интерактивной ОС, предоставляющей уникальные возможности в части выполнения различных операционных сред на одном ...
... , может приводить к большим потерям рабочего тела и раскрутке космического аппарата до недопустимых угловых скоростей. Таким образом разработка алгоритмов контроля и диагностики системы управления ориентацией космического аппарата – является актуальной задачей. В настоящей работе решается задача построения алгоритмов контроля и идентификации отказов командных приборов и исполнительных органов. ...



0 комментариев