Найдите решение по доминированию в данной игре

1.  Найдите решение по доминированию в данной игре

	a	b	c	d
A	2 5	6 2	4 1	3 0
B	1 4	4 3	1 2	2 1
C	0 1	1 1	5 1	1 5
D	3 2	1 0	2 0	4 4

Решение:

1.  В исходной игре стратегия d строго доминирует стратегию a. Больше строго или нестрого доминирующих стратегий у первого или второго игрока нет. Очевидно, что второй игрок не будет играть стратегию a и ее можно исключить.

Получаем:

	b	c	d
A	6 2	4 1	3 0
B	4 3	1 2	2 1
C	1 1	5 1	1 5
D	1 0	2 0	4 4

2.  В получившейся игре видим, что стратегия С первого игрока строго доминирует стратегию D. А также стратегия В строго доминирует стратегию А. Рассмотрим оба варианта. В первом – вычеркиваем стратегию D, во втором – стратегию А.

Получаем:

	b	c	d
A	6 2	4 1	3 0
B	4 3	1 2	2 1
C	1 1	5 1	1 5
	b	c	d
B	4 3	1 2	2 1
C	1 1	5 1	1 5
D	1 0	2 0	4 4

3.  В полученной игре в обоих вариантах получаем, что у второго игрока нет строго доминирующих стратегий. Однако в первом варианте у второго игрока есть нестрого доминирующая стратегия b (доминирует стратегию d). Во втором же варианте у второго игрока нет строго или нестрого доминирующих стратегий. Однако по-прежнему есть строго доминирующая стратегия C первого игрока, которая доминирует стратегию D.

Продолжим рассматривать 2 варианта игры: в первом варианте вычеркиваем стратегию d, а втором – стратегию D. Получим 2 игры:

	b	c
A	6 2	4 1
B	4 3	1 2
C	1 1	5 1

	b	c	d
B	4 3	1 2	2 1
C	1 1	5 1	1 5

4.  В первом варианте полученной новой игры видим, что стратегия B первого игрока строго доминирует и стратегию А и стратегию C. Во втором же варианте видим, что стратегия b второго игрока нестрого доминирует стратегию d. Исключив в первом варианте стратегию A получим новую игру, совпадающую с вариантом, если во втором варианте исключить стратегию d. Еще один вариант игры получается исключением стратегии С в первом варианте игры. Итого вновь имеем 2 возможных варианта игры.

	b	c
B	4 3	1 2
C	1 1	5 1

	b	c
A	6 2	4 1
B	4 3	1 2

5.  В первом варианте получившейся игры видим, что у второго игрока нет доминирующих стратегий. Во втором же варианте он имеет строго доминирующую стратегию b (доминирует стратегию с). Однако в первом варианте у первого игрока остается строго доминирующая стратегия B (доминирует стратегию С).

Исключим в первом варианте стратегию С, во втором – с.

	b	c
B	4 3	1 2

	b
A	6 2
B	4 3

6.  В первом варианте стратегия b второго игрока строго доминирует стратегию с. Во втором варианте стратегия B первого игрока строго доминирует стратегию А. Вычеркнув в обоих вариантах строго доминируемые стратегии, получим одинаковый вариант игры:

	b
B	4 3

На основании этого можно сделать вывод, что в исходной игре должен реализоваться исход (B, b).

2. Заполните пропуски в таблице так, чтобы в этой игре в чистых стратегиях было бы 3 равновесия по Нэшу. Найдите все равновесия в смешанных стратегиях (любым способом).

	a	b
A	7 ?	? 4
B	? 25	9 ?

Решение:

Заменим знаки вопроса на неизвестные переменные следующим образом:

	a	b
A	7 y	x 4
B	t 25	9 z

Попытаемся заполнить пропуски в таблице так, чтобы равновесия по Нэшу достигались в вариантах игры (A, a), (B, a), (B, b), а при игре (A, b) равновесие по Нэшу не достигалось. Тогда должна выполняться система неравенств (объедим их парами для каждого варианта игры):

 Откуда получаем:  

Возьмем минимальные целые числа, удовлетворяющие системе неравенств. Получим игру:

	a	b
A	7 25	6 4
B	9 25	9 5

Действительно, в данной игре варианты (A, a), (B, a), (B, b) будут являться равновесиями по Нешу, т.к. здесь ни одному из игроков не выгодно изменить свою стратегию, а при игре (A, b) каждому из игроков выгодно изменить свою стратегию.

Найдем равновесие в смешанных стратегиях. Предположим, что первый игрок с вероятностью µ играет стратегию A, соответственно с вероятностью (1 - µ) – стратегию B. Второй игрок с вероятностью ν играет стратегию a, а с вероятностью (1 - ν) - стратегию b. Тогда функции выигрыша игроков будут выглядеть следующим образом:

;

Тогда функции отклика будут следующими:

 

Имеем 2 равновесия в смешанных стратегиях. Если второй игрок играет стратегию b, то первый игрок всегда будет играть стратегию B. Если первый игрок играет стратегию А, то второй игрок будет играть стратегию a.

Решением же в доминируемых стратегиях будет (B, a).

3. Двое бегут по лыжной трассе навстречу друг другу. У каждого лыжника 2 стратегии: «уступить» (У) и «не уступить» (Н). Если один из игроков уступает другому, то его потери - 9 секунд, второй – не теряет ничего; если же лыжники сталкиваются, то оба теряют 25 секунд.

d)  Составьте платежную матрицу этой игры. Найдите равновесия в чистых стратегиях.

e)  Нарисуйте линии откликов игроков и найдите смешанные равновесия в этой игре.

f)  Допустим теперь, что у игроков теперь 3 стратегии: «не уступить», «уступить» и «уступить пол-лыжни». Если оба уступили друг другу пол-лыжни, то потери каждого 4 секунд, если же один уступил пол-лыжни, а второй - нет, то лыжники столкнутся, и потери при столкновении у уступившего – 29 секунд, у неуступившего - 4 секунды. Найдите все равновесия по Нэшу (в чистых и в смешанных стратегиях).

Решение:

a)  Составим платежную матрицу этой игры:

	У	Н
У	-9 -9	0 -9
Н	-9 0	-25 -25

В чистых стратегиях равновесия в данной игре нет.

b)  Найдем равновесие в смешанных стратегиях.

Предположим, что первый игрок с вероятностью µ играет стратегию У, соответственно с вероятностью (1 - µ) – стратегию Н. Второй игрок с вероятностью ν играет стратегию У, а с вероятностью (1 - ν) - стратегию Н.

Функции выигрыша игроков:

Соответственно функции откликов:

 

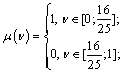
Имеем 2 точки пересечений линий, соответствующие равновесиям в смешанных стратегиях:

2.  (Н; У), то есть первый игрок всегда не уступает, а второй – уступает;

3.  (У; Н), то есть первый игрок всегда уступает, а второй – не уступает;

4.  Каждый из игроков с вероятность 16/25 уступает лыжню и с вероятностью 9/25 не уступает лыжню.

c)  Составим платежную матрицу игры:

	У	Н	УП
У	-9 -9	0 -9	-4 -9
Н	-9 0	-25 -25	-29 -25
УП	-9 -4	-25 -29	-4 -4

В чистых стратегиях равновесия нет.

4. Профсоюз заключает с фирмой соглашение на несколько лет об уровне заработной платы w>0. Профсоюз максимизирует функцию совокупной прибыли членов профсоюза (зарплата за вычетом издержек от работы): u(w,L)=wL-4*L², фирма максимизирует свою прибыль (выпуск за вычетом зарплаты): П(w,l)=7*L^0.5-wL.

d)  Найти равновесный уровень заработной платы и занятости в статической игре.

e)  Каково равновесие в динамической игре, если профсоюз достаточно мощный, чтобы навязать фирме любой уровень заработной платы, после чего фирма не может менять уровень заработной платы в течение срока контракта, но может нанимать любое количество труда L>0.

f)  Каково равновесие в динамической игре, если фирма – монополист на рынке труда, и она может установить любую заработную плату, после чего профсоюз может только регулировать численность работающих на монополиста.

Решение:

b)  Профсоюз устанавливает уровень заработной платы. В свою очередь исходя из этого значение фирма определяет количество занятых. Предположим, что профсоюз установил уровень заработной платы w^*. Тогда прибыль фирмы будет П(w^*,l)=7*L^0.5- w^*L. Максимизируем прибыль по L.

П_L’(w^*,l)= 3.5L^-0.5 – w^* = 0 при L^*=.

То есть при установлении профсоюзом уровня з/п в значение w^* фирма примет решении о найме рабочей силы в значение L^*=.

Максимизируем теперь функцию совокупной прибыли членов профсоюза u(w,L)=wL-4*L²

Подставим в функцию найденное на предыдущем шаге значение L^*.

u(w,L^*)=wL^*4*L^*2=

. , откуда .

Решение игры: .

c)  В данном случае сначала фирма устанавливает уровень з/п. После чего профсоюз принимает решение о количестве занятых, максимизируя свою прибыль. Предположим, что фирма приняла решение об уровне з/п равным w^*.

Тогда прибыль членов профсоюза будет определяться: u(w^*,L)=w^*L-4*L². Профсоюз максимизирует свою прибыль, варьируя значение L.

, откуда максимизирующий прибыль сотрудников профсоюза уровень занятости определяется как . Подставим это значение в функцию прибыли фирмы:

П(w, L^*)=7*L^*0.5-wL^*=. П_w’(w, L^*)==0 при .

Соответственно .

Решение игры: (;).

5. В этой игре с нулевой суммой найдите равновесие в осторожных стратегиях. Существует ли в этой игре равновесие по Нэшу в чистых стратегиях?

	c1	c2	c3	c4	c5
s1	5	2	3	6	4
s2	4	1	1	5	0
s3	6	0	4	9	-3

Решение:

Игра антагонистическая, значит можем найти MinMax и MaxMin и сравнить их.

MaxMin = Max (2, 0, -3) = 2 и соответствует s1.

MinMax = Min (6, 2, 4, 9, 4) = 2 и соответствует c2.

Получаем, что MinMax = MaxMin = 2, следовательно в игре существует равновесие по Нэшу в чистых стратегиях и соответсвует (s1, c2).

6. На корабле 50 пиратов делят 100 кусков золота по следующему правилу: первым дележ предлагает капитан. Если хотя бы половина команды (включая капитана) согласна, то на этом игра и заканчивается. Если нет, то капитана выбрасывают за борт и дележ предлагает следующий по старшинству и т.д. Найдите совершенное подыгровое равновесие в этой игре.

Решение:

Будем использовать метод обратной индукции. Упорядочим всех пиратов по старшинству.