Этап. Рассмотрим данный метод на задаче под названием «орлянка»

2 этап. Рассмотрим данный метод на задаче под названием «орлянка»

Пример 6.1: Два игрока независимо друг от друга называют числа, если оба числа имеют одинаковую четность, то один получает рубль, если разные, то рубль получает второй.

Решение: Данная игра представлена матрицей А

Здесь игрок 1 и 2 имеет две чистые стратегии. Решаем игру с позиции первого игрока.

Пусть его стратегия х = (α, 1-α), 0 ≤α≤1.

Вычислим хА=(α, 1-α)(1 -1)= (α- (1-α), -α+1-α)=(2α-1, 1-2α). (-1 1)

Обозначим f₂(α)=2α-1 и f₂(α)=1-2α.

Найдем max min (f₁ (α), f₂ (α))= max( min(2α-1, 1-2α)).

Для нахождения максимина приведем графическую иллюстрацию (1)

Вначале для каждого α ? [0,1] найдем min(2α-1, 1-2α). На рисунке (1) такие минимумы для каждого α ? [0,1] образуют ломанную – нижнюю огибающую MPQ. Затем на огибающей находим наибольшее значение, которое будет в точке P. Эта точка достигает при α ? [0,1], которое является решением уравнения f₁ = f₂ , т.е. 2α-1= 1-2α. Здесь α=1/2. Вторая координата точки P будет 2*1/2-1=0. итак P(1/2, 0). В смешанном расширении данной игры max( min(2α-1, 1-2α))=0.

Максиминная стратегия первого игрока х_н = (α, 1-α)=(1/2, 1/2). По аналогичной схеме найдем минимаксную стратегию второго игрока. Его стратегию обозначим y=(β, 1-β), 0≤β≤1.

Вычислим Аy=( 2β-1, 1-2β).

Обозначим f₁(β)= 2β-1, f₂(β)= 1-2β

Найдем min max (f₁(β), f₂(β))= min (max (2β-1, 1-2β)).

Проведем геометрическую иллюстрацию на рисунке 2.

Для каждого β?[0,1] найдем min(2β-1, 1-2β).

На рисунке (2) такие минимумы для каждого β ? [0,1] образуют ломанную – верхнюю огибающую RST. Затем на огибающей находим наименьшее значение, которое будет в точке S. Координаты точки S(1/2,0).

В смешанном расширении данной игры min (max (2β-1, 1-2β))=0.

Y^В=( β, 1-β)=(1/2, 1/2) и выполняется условие, что

V_H = max min а_ij =min max а_ij = V^в. Значит цена игры V^* =0 и седловая точка равна (х^*, у^*) = ((1/2, 1/2), (1/2, 1/2)).

Ответ: (х^*, у^*)=((1/2, 1/2), (1/2, 1/2)), V^* =0.

3 этап. Учитель повторяет последовательность решения данной задачи графоаналитическим методом. Дает домашнее задание.

Домашнее задание: придумать каждому ученику 1 задачу, чтобы она решалась графоаналитическим методом.

Задача:

Графоаналитическим методом найти цену и седловую точку матричной игры, заданную матрицей выигрыша первого игрока.

> with(simplex):

> A := Matrix(4,4, [[4, 2,3,-1],[-4,0,-2,2],[-5,-1,-3,-2],[-5,-1,-3,-2]]);

 

>

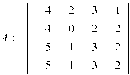
C:={ A[1,1]*x+A[1,2]*y+A[1,3]*z+A[1,4]*t <=1,

A[2,1]*x+A[2,2]*y+A[2,3]*z+A[2,4]*t <=1,

A[3,1]*x+A[3,2]*y+A[3,3]*z+A[3,4]*t

<=1,A[4,1]*x+A[4,2]*y+A[4,3]*z+A[4,4]*t <=1};

 

Ø X:=maximize(f,C ,NONNEGATIVE );

> f_max:=subs(X,f);

>

> XX:=X*V;

>

Ø C1:={ A[1,1]*p1+A[2,1]*p2+A[3,1]*p3+A[4,1]*p4 >=1,

Ø A[1,2]*p1+A[2,2]*p2+A[3,2]*p3+A[4,2]*p4 >=1,

Ø A[1,3]*p1+A[2,3]*p2+A[3,3]*p3+A[4,3]*p4

Ø >=1,A[1,4]*p1+A[2,4]*p2+A[3,4]*p3+A[4,4]*p4 >=1};

Ø Y:=minimize(f1,C1 ,NONNEGATIVE);

>

>

Ø YY:=V*Y;

>

> VV:=XX*V*L;

 

Занятие №3 Решение систем неравенств графическим методом

 

Тип урока: урок изучения нового материала.

Вид урока: Лекция, урок решения задач.

Продолжительность: 2 часа.

Цели:1) Изучить графический метод.

2) Показать применение программы Maple при решении систем неравенств графическим методом.

3)Развить восприятие и мышление по данной теме.

План занятия: 1 этап: изучение нового материала.

2 этап: Отработка нового материала в математическом пакете Maple.

3 этап: проверка изученного материала и домашнее задание.

Ход занятия.

1 этап: Графический метод заключается в построении множества допустимых решений ЗЛП, и нахождении в данном множестве точки, соответствующей max/min целевой функции.

В связи с ограниченными возможностями наглядного графического представления данный метод применяется только для систем линейных неравенств с двумя неизвестными и систем, которые могут быть приведены к данному виду.

Для того чтобы наглядно продемонстрировать графический метод, решим следующую задачу:

1.  На первом этапе надо построить область допустимых решений. Для данного примера удобнее всего выбрать X2 за абсциссу, а X1 за ординату и записать неравенства в следующем виде:

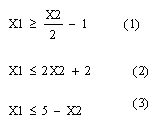
Так как  и  графики и область допустимых решении находятся в первой четверти. Для того чтобы найти граничные точки решаем уравнения (1)=(2), (1)=(3) и (2)=(3).

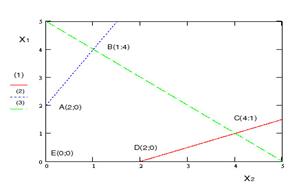
Как видно из иллюстрации многогранник ABCDE образует область допустимых решений.

Если область допустимых решений не является замкнутой, то либо max(f)=+ ∞, либо min(f)= -∞.