Навигация
Понятие управляемости системы
3.6. Понятие управляемости системы
Пусть линейный многомерный процесс описывается векторным дифференциальным уравнением
dx(t)/dt=Ax(t)+Dm(t), (10)
где x – n-мерный вектор состояния; m – r-мерный вектор, представляющий управляющие воздействия; A – квадратная матрица коэффициентов n-го порядка; D – матрица управления размера nxr.
Матрица A может быть приведена к диагональной матрице (или в общем случае к жордановой форме)

где lш – собственные значения матрицы A, которые предполагаются все различными.
Применяя подстановку x=Tz, исходное уравнение запишется в канонической форме
dz(t)/dt=Lz(t)+Dm(t),
где D=T-1D=[dij]nxr.
Вектор z в полученной формуле будем называть каноническим вектором состояния. Будем считать, что в предыдущих матричных выражениях собственные значения li расположены в порядке возрастания их модулей, комплексные li – в порядке возрастания их аргументов, векторы-столбцы матрицы T – нормализованы, то есть выбраны так, что евклидова длина их равна единице.
Запишем полученное выражение в развернутой форме, то есть в виде системы дифференциальных уравнений первого порядка:
![]()
Эти уравнения показывают, что управляющее воздействие mk не будет оказывать какого-нибудь влияния на движение по координате zj, если
![]()
то есть когда djk=0 для k=1, 2, …, r. Запись в такой форме означает, что все элементы j-й строки матрицы D все равны нулю. Отсюда следует вывод, что неуправляемыми координатами системы являются все те канонические координаты, которые соответствуют нулевым строкам матрицы D. Равенство нулю всех элементов этих строк матрицы D делает невозможным управление по соответствующим координатам. Это означает также, что изменение координат происходит независимо от управляющих воздействий и, следовательно, целиком определяется начальными условиями и возмущениями. Можно сказать, что эти координаты развязаны от управления.
Приведенное рассмотрение позволяет дать следующее определение управляемости: процесс, описываемый уравнением (10), является полностью управляемым, если матрица D не содержит строк, элементы которых равны нулю; координаты, соответствующие ненулевым строкам D, считаются управляемыми.
3.7. Описание непрерывных систем с помощью одного дифференциального уравнения
Непрерывную систему часто описывают дифференциальным уравнением относительно ее выхода y(t) и входа r(t):
![]()
или, вводя оператор дифференцирования p=d/dt,
![]()
Здесь мы ввели функцию F(t)=B(p)v(t), потому что, как правило, входное воздействие на систему известно. Такая система называется системой «вход–выход».
Многочлен A(p) называется собственным оператором системы, а M(p) – входным оператором.
Введем понятие передаточной функции системы. Отношение входного оператора М(р) к собственному оператору D(р) назовем передаточной функцией W(р) системы, описываемого линейным дифференциальным уравнением с постоянными коэффициентами
![]()
Решение этой системы совершенно аналогично решению линейного неоднородного дифференциального уравнения с постоянными коэффициентами.
3.8. Переход от системы дифференциальных уравнений к одному уравнению
Введем оператор дифференцирования Lij=anijpn+a(n-1)ijpn-1+…+a1ijp1+a0ij. Тогда любую систему дифференциальных уравнений (в том числе и систему уравнений, описывающих систему «вход–состояние–выход») можно представить в виде
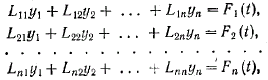
Так как операторы Lij зависят только от p, то решение можно получить, используя формулы Крамера:
![]()
где D(p) – дифференциальный оператор, определяемый определителем:

![]() – оператор, определяемый ki-ым алгебраическим дополнением.
– оператор, определяемый ki-ым алгебраическим дополнением.
3.9. Переход от одного уравнения к системе дифференциальных уравнений
Пусть дана линейная система с постоянными параметрами, одним входом и выходом:
![]()
где p=d/dt. Непосредственно из схемы моделирования следует
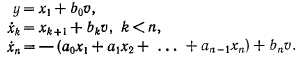 (11)
(11)
Дифференцируя y, получим
![]()
Последующая подстановка px1 из полученных уравнений дает
![]()
Согласно приводимой процедуре вторая и старшие производные y равны

Подставив полученные выражения для y, py, …, pn-1y и выражения (11) в исходное уравнение и сопоставляя с выражением для pny, получим выражения для ai и bi:

bi , по-видимому, можно также записать в виде

Значит, bi можно определить, умножив обе части этого выражения на обратную матрицу коэффициентов. Согласно полученным выражениям, одна из форм матриц A, B, C, D для системы вида «вход–состояние–выход» имеет вид
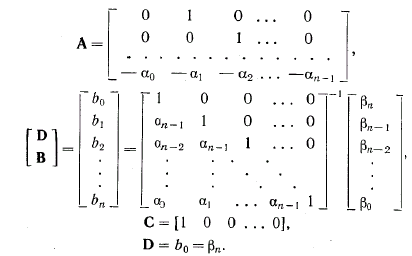
Приведенные уравнения состояния соответствуют так называемому стандартному виду системы.
Список литературы:
1. Чемоданов Б К. Математические основы теории систем.
2. Ю. Ту. Современная теория управления.
Похожие работы
... . , т.е. таких уравнений, у которых правая часть не является ненпрерывной по x функций рассмотрены в статье [5]. Теория систем автоматического управления, описываемых дифференциальными уравнениями с разрывными правыми частями рассматривается в книгах [13, 14, 15]. В работе С.В. Емельянова [13] излагается один из разделов теории автоматичесеого управления – теория систем с переменной структурой, ...
... популяции обязательно вырождаются, причем независимо от начального распределения особей по возрасту. В завершение рассмотрим пример. Одной из классических моделей динамики популяций является так называемая логистическая модель или модель Ферхюльста, которая описывается дифференциальным уравнением с начальным условием , где , см., например, [5, c. 14]. Если учитывать ограниченность времени жизни ...
... в руки инженера эффективную вычислительную процедуру решения задачи оптимизации управления, хорошо приспособленную к использованию ЭВМ. Этот метод мы рассмотрим более подробно. 2.4. Метод динамического программирования 2.4.1. Дискретная форма вариационной задачи Преодоление рассмотренных трудностей решения вариационной задачи лежит на путях использования эффективных вычислительных методов ...
... - α) / (2 + α)) yk - 1 + (α/ (2 + α)) (xk + xk - 1). (9) В лабораторной работе производится оценка ошибок цифрового моделирования для каждого из этих методов. Моделирование линейных замкнутых систем Нужно быть очень внимательным при выборе интервала дискретизации, когда моделируются замкнутые системы. В этих системах текущее значение входного процесса сравнивается со ...




0 комментариев