Навигация
2.7.5. Формула Коши
При помощи формулы Коши можно выразить решение линейной неоднородной системы дифференциальных уравнений через некоторую фундаментальную систему решений соответствующей однородной линейной системы.
Рассмотрим неоднородную линейную систему дифференциальных уравнений (2), записанную в векторном виде
![]()
Соответствующая ей однородная система (3)
![]()
Пусть x1, x2, …, xn – фундаментальная система решения системы уравнений (3). Образуем матрицу X1(t), столбцы которой являются этими решениями:

Определитель матрицы Х1(t) представляет собой определитель Вронского. Он отличен от нуля для всех tÎ[a, b]. Следовательно, существует обратная матрица X-11(t) при каждом tÎ[а, b]. Составим матрицу
X(t, t0) = X1(t)X1-1(t0)
Столбцы этой матрицы также образуют фундаментальную систему решений системы уравнений (3). Отметим, что X(t, t0)=![]() Назовем матрицу X(t, t0) фундаментальной матрицей системы (3). Эта матрица удовлетворяет матричному уравнению
Назовем матрицу X(t, t0) фундаментальной матрицей системы (3). Эта матрица удовлетворяет матричному уравнению
![]()
Решение x(t) системы уравнений (3), удовлетворяющее начальным условиям x(t0)=x0, можно записать в виде
![]()
Тогда можно показать, что следующая формула, называемая формулой Коши, позволяет найти решение x(t) неоднородной системы (2), удовлетворяющее начальным условиям x(t0)=x0, если известна фундаментальная матрица X(t, t0) однородной системы (3):
![]()
Следует отметить, что если матрица А постоянная, т. е. рассматриваемая система дифференциальных уравнений является системой линейных уравнений с постоянными коэффициентами
![]()
то решение этой системы x(t), удовлетворяющее начальным условиям x(t0)=x0, запишется в виде
![]()
где X (f) — матрица, столбцы которой состоят из фундаментальной системы решений однородной системы уравнений xt'=Ах, причем X (t0) = E.
2.7.6. Линейное уравнение n-го порядка
Линейное уравнение n-го порядка имеет вид
![]()
где a0(t), …, an(t) — непрерывные функции для tÎ(a, b), причем а0(t)¹0. Соответствующее этому уравнению однородное уравнение имеет вид
![]()
Эти уравнения путем введения вспомогательных функций
![]()
можно свести соответственно к системам уравнений

или в векторной форме,

Пусть начальные условия этой системы имеют вид
![]()
Эта система имеет единственное решение

Для нахождения частного решения ф(t) данного уравнения можно использовать метод вариации произвольных постоянных. При этом система алгебраических уравнений для нахождения сi'(t) имеет следующий вид:

Определитель этой системы есть определитель Вронского для линейно независимой системы решений x1 ,…, xn, поэтому W(t)¹0, и данная система имеет единственное решение. Интегрируя полученные значения для c'i(t), найдем ci(t) и тогда искомое решение
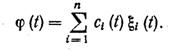
Решение x(t) исходного уравнения, удовлетворяющее заданным условиям, найдется по формуле Коши
![]()
где
![]()
где ci(t) определяются из системы уравнений

Определитель этой системы представляет собой определитель Вронского фундаментальной системы решений x1, …, xn и поэтому не равен нулю. Эта система имеет единственное решение c1(t), …, cn(t). Следовательно, решение x1(t, t) определяется единственным образом.
Похожие работы
... . , т.е. таких уравнений, у которых правая часть не является ненпрерывной по x функций рассмотрены в статье [5]. Теория систем автоматического управления, описываемых дифференциальными уравнениями с разрывными правыми частями рассматривается в книгах [13, 14, 15]. В работе С.В. Емельянова [13] излагается один из разделов теории автоматичесеого управления – теория систем с переменной структурой, ...
... популяции обязательно вырождаются, причем независимо от начального распределения особей по возрасту. В завершение рассмотрим пример. Одной из классических моделей динамики популяций является так называемая логистическая модель или модель Ферхюльста, которая описывается дифференциальным уравнением с начальным условием , где , см., например, [5, c. 14]. Если учитывать ограниченность времени жизни ...
... в руки инженера эффективную вычислительную процедуру решения задачи оптимизации управления, хорошо приспособленную к использованию ЭВМ. Этот метод мы рассмотрим более подробно. 2.4. Метод динамического программирования 2.4.1. Дискретная форма вариационной задачи Преодоление рассмотренных трудностей решения вариационной задачи лежит на путях использования эффективных вычислительных методов ...
... - α) / (2 + α)) yk - 1 + (α/ (2 + α)) (xk + xk - 1). (9) В лабораторной работе производится оценка ошибок цифрового моделирования для каждого из этих методов. Моделирование линейных замкнутых систем Нужно быть очень внимательным при выборе интервала дискретизации, когда моделируются замкнутые системы. В этих системах текущее значение входного процесса сравнивается со ...




0 комментариев