Навигация
Понятие пространства состояний
3.2. Понятие пространства состояний
С точки зрения анализа и синтеза систем представляется целесообразным разделить все переменные, характеризующие систему, на три группы:
1) входные переменные или входные воздействия mi, представляющие сигналы, генерируемые системами, внешними по отношению к исследуемой, и влияющие на поведение системы;
2) выходные переменные или переменные, характеризующие реакцию системы yj, позволяющие описать некоторые аспекты поведения системы, представляющие интерес для исследователя;
3) переменные (координаты) состояния или промежуточные переменные xk, характеризующие динамическое поведение исследуемой системы.
Величины mi, yj и xk предполагаются функциями времени. Для удобства оперирования с многомерными величинами совокупность входных переменных представим в виде вектора входа, совокупность выходных переменных – в виде вектора выхода, и совокупность переменных состояния – в виде вектора состояния:
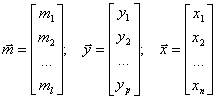 .
.
Множество всех значений, которые может принять вектор входа m в момент t, образует пространство входа системы. Множество всех значений, которые может принять вектор выхода y в момент t, образует пространство выхода системы. Множество всех значений, которые может принять вектор состояния x в момент t, образует пространство состояний системы.
3.3. Описание непрерывных систем с помощью системы дифференциальных уравнений
В любой момент времени t состояние системы является функцией начального состояния x(t0) и вектора входа m(t0, t), то есть
x(t)=F[x(t0); m(t0; t)],
где F – однозначная функция своих аргументов. Вектор выхода в момент t является также функцией x(t0) и m(t0; t) и может быть записан как
y(t)=z[x(t0); m(t0; t)].
Эти два уравнения часто называют уравнениями состояния системы. Для систем, описываемых дифференциальными уравнениями, эти уравнения могут быть записаны в следующей общей форме:
x(t)=F[x(t); m(t)],
y(t)=z[x(t); m(t)].
Такое описание системы носит название «вход–состояние–выход».
Если система описывается линейными дифференциальными уравнениями, то уравнения состояния системы сводятся к следующим:
dx(t)/dt=A(t)x(t)+D(t)m(t);
y(t)=B(t)x(t)+G(t)m(t),
где A(t) – матрица коэффициентов; D(t) – матрица управления; B(t) – матрица выхода; G(t) – матрица обхода системы.
Решение этой системы будем искать в форме
x(t)=p(t–t0)C1(t), (7)
где p(t–t0)=exp A(t–t0) – матрица перехода процесса, а С1(t) – вектор, зависящий от времени, заменяющий вектор начального состояния x0 в уравнении движения при отсутствии внешних воздействий. Дифференцируя это выражение по t, получаем
dx(t)/dt=Ax(t)+p(t–t0)dC1(t)/dt.
Если формула (7) является решением однородного уравнения, то величины в правых частях однородного уравнения и полученной формулы должны быть одинаковы. Отсюда
Dm(t)=p(t–t0)dC1(t)/dt.
Решая это уравнение относительно С1(t), получаем
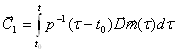
Учитывая это выражение и определение матрицы перехода уравнение (7) приведем к виду

При t=t0, p(t–t0)=I и С2=x(t0). Отсюда находим

3.4. Описание систем переменными состояния
Линейная стационарная система может быть описана совокупностью линейных дифференциальных уравнений первого порядка с постоянными коэффициентами, которую можно представить в следующей векторно-матричной форме:
dv(t)/dt=Av(t),
где A – матрица коэффициентов; v(t) – вектор-столбец, представляющий собой входные переменные mi и координаты xk системы
![]()
Если входные переменные рассматривать совместно с переменными состояния системы, то есть включить их в число координат системы, то вектор v можно считать вектором состояния системы увеличенной размерности.
3.5. Понятие наблюдаемости системы
Перепишем еще раз выражение для вектора выхода линейного многомерного процесса:
y(t)=Bx(t)+Gm(t), (8)
где y – p-мерный вектор, представляющий выходные переменные; B – матрица выхода размером pxn; G – матрица обхода системы размера pxr.
Пусть матрица B имеет вид

а матрица обхода G задана в виде

Тогда, развертывая формулу (8), получаем p выражений
![]() (9)
(9)
Координату состояния принято называть наблюдаемой, если она может быть определена или для нее может быть получена оценка по измеримым выходным переменным. Анализ уравнений (9) показывает, что координата xk может быть определена или для нее может быть получена оценка по измеримым выходным переменным y1, y2, …, yi, …, yp, если коэффициенты bik для i=1, 2, …, p не все равны нулю. Другими словами, xk является наблюдаемой координатой, если элементы k-го столбца матрицы выхода не все равны нулю. Если это условие не соблюдается, то координату xk называют ненаблюдаемой. Таким образом, линейный процесс является наблюдаемым, если матрица выхода B не содержит столбцов, элементы которых равны нулю.
Похожие работы
... . , т.е. таких уравнений, у которых правая часть не является ненпрерывной по x функций рассмотрены в статье [5]. Теория систем автоматического управления, описываемых дифференциальными уравнениями с разрывными правыми частями рассматривается в книгах [13, 14, 15]. В работе С.В. Емельянова [13] излагается один из разделов теории автоматичесеого управления – теория систем с переменной структурой, ...
... популяции обязательно вырождаются, причем независимо от начального распределения особей по возрасту. В завершение рассмотрим пример. Одной из классических моделей динамики популяций является так называемая логистическая модель или модель Ферхюльста, которая описывается дифференциальным уравнением с начальным условием , где , см., например, [5, c. 14]. Если учитывать ограниченность времени жизни ...
... в руки инженера эффективную вычислительную процедуру решения задачи оптимизации управления, хорошо приспособленную к использованию ЭВМ. Этот метод мы рассмотрим более подробно. 2.4. Метод динамического программирования 2.4.1. Дискретная форма вариационной задачи Преодоление рассмотренных трудностей решения вариационной задачи лежит на путях использования эффективных вычислительных методов ...
... - α) / (2 + α)) yk - 1 + (α/ (2 + α)) (xk + xk - 1). (9) В лабораторной работе производится оценка ошибок цифрового моделирования для каждого из этих методов. Моделирование линейных замкнутых систем Нужно быть очень внимательным при выборе интервала дискретизации, когда моделируются замкнутые системы. В этих системах текущее значение входного процесса сравнивается со ...




0 комментариев