Навигация
Операция сопряжения и ее свойства
3. Операция сопряжения и ее свойства.
Для данного комплексного числа z=x+iy число x-iy (отличающееся от z лишь знаком при мнимой части) называется сопряженным и обозначается символом z. Переход от числа z к числу z называется сопряжением, а сами эти числа сопряженными (друг к другу), т.к. (z)=z. Из определения следует, что только действительное число сопряжено самому себе. Геометрически сопряженные числа изображаются точками, симметричными относительно действительной оси (рис.2).
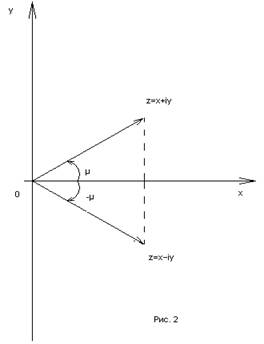
Отсюда следует, что |z|=|z|, argz=-argz. Кроме того,
![]() z+z=2x=2Rez;
z+z=2x=2Rez;
z-z=2iy=2iImz;
zz=x2+y2=|z|2,
а также: z1+z2=z1+z2; z1z2=z1z2; (z1/z2)=z1/z2; P(z)=P(z), где Р (z) – любой многочлен с действительными коэффициентами; (P(z)/Q(z))=(P(z)/Q(z)), где P и Q – многочлены с действительными коэффициентами.
4. Извлечение корней.
Извлечение корня из комплексного числа есть действие, обратное возведению в степень. С его помощью по данной степени (подкоренное число) и данному показателю степени (показатель корня) находят основание (корень). Иначе говоря, это действие равносильно решению уравнения zn=a для нахождения z. В множестве комплексных чисел действие извлечения корня всегда выполнимо, хотя причем и неоднозначно: в результате получается столько значений, каков показатель корня. В частности, квадратный корень имеет ровно два значения, которые можно найти по формуле:
√a=√α+iβ=±((√|a|+α)/2 ± i(√|a|-α)/2)), где знак «+» в скобках берется при β>0, «-» - при β<0.
5. Геометрический смысл алгебраических операций.
Пусть даны два комплексных числа z1 и z2. В результате сложения этих чисел получается число z3, изображаемое вектором 0С диагонали параллелограмма 0АСВ (по правилу параллелограмма сложения векторов): z1+z2=0A+0B=0C=z3.
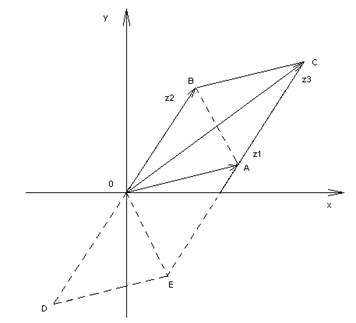 Рис.3
Рис.3
Разность (z1-z2) данных чисел, соответствующая их вычитанию, можно рассматривать как сумму вектора 0А, изображающего число z1 и вектора 0D=--0В, противоположного вектору 0В (симметричного ему относительно начала координат): z1-z2=z1+(-z2)=0A+0D=0E=BA. Таким образом, разности (z1-z2) данных чисел соответствует вектор ВА другой диагонали параллелограмма 0АСВ.
Для иллюстрации остальных алгебраических действий над комплексными числами более удобна тригонометрическая форма.
Умножение. Пусть даны два комплексных числа z1=r1(cosφ1+isinφ1) и z2=r2(cosφ2+isinφ2). Перемножая их получим z1z2=r1r2(cos(φ1+φ2)+isin(φ1+φ2)). Следовательно, при умножении комплексных чисел их модули перемножаются, а аргументы складываются. Это правило верно и для любого числа сомножителей.
Деление. Если требуется разделить z1 на z2, то выполняем следующие преобразования: z1/z2=(z1z2)/(z2z2)=(r1(cosφ1+isinφ1)r2(cosφ2-isinφ2))/ (r2(cosφ2+isinφ2)r2(cosφ2-isinφ2))=(r1/r2)(cos(φ1-φ2)+isin(φ1-φ2)), т.е. при делении двух комплексных чисел их модули делятся, а аргументы вычитаются.
Возведение в степень. Умножая число z=r(cosφ+isinφ) само на себя «n» раз, получаем согласно правилу умножения zn=rn(cosφ+isinφ)n=rn(cosnφ+isinnφ). Таким образом, при возведении комплексного числа в степень «n» в ту же степень возводимся его модуль, а аргумент умножается на «n» (на показатель степени). В частном случае, если r=1, то предыдущее равенство принимаем вид (cosφ+isinφ)n= cosnφ+isinnφ (9). Полученная формула называется формулой Муавра (1667-1754).
Извлечение корня. Пусть а=reiφ, z=ρeiσ. Решаем уравнение zn=a для вычисления n√a: ρneinσ=reiφ. Отсюда с учетом того, что аргументы чисел отличаются на целое кратное числу 2π, получаем: ρn=r, nσ-φ=2πK, или ρ=n√r; σK+1=(φ+2πK)/n (причем К=0,1,2…n-1). Таким образом, zk=n√r(cosφ+isinφ)=n√r((cosφ+2Kπ)/n+isin(φ+2Kπ)/n)) (10), где n√r , - арифметический корень, а К=0,1,2,…,n-1; т.е. корень степени n в множестве комплексных чисел имеет “n” различных значений zk (исключение представляет z=0. В этом случае все значения корня равны между собой и равны нулю).
Заметим также, что разность между аргументами соседних чисел zk+1 и zk постоянна и равна 2π/n: σk+1-σk=(φ+2π(K+1))/n-(φ+2πK)/n=2π/n. Отсюда следует, что все значения n√a располагаются на комплексной плоскости в вершинах некоторого правильного n-угольника с центром в начале координат.
IV. Применение комплексных чисел к решению алгебраических уравнений 3-ей и 4-ой степеней.
Похожие работы
... повышенным риском как для заемщиков, так и для кредиторов (18, 38). Таким образом, наиболее серьезными и объективными препятствиями для успешного и быстрого развития системы ипотечного кредитования в России является экономическая нестабильность, проблемы формирования среднего класса, низкий уровень жизни населения. Кроме того, государство должно оказать зримую государственную поддержку банкам, ...
... предполагает: использование различных, взаимодополняющих источников информации; сочетание ретроспективного анализа с прогнозом показателей, характеризующих конъюнктуру рынка; применение совокупности различных методов анализа и прогнозирования. При изучении конъюнктуры товарного рынка ставится задача не только определения состояния рынка на тот или иной момент, но и предсказания вероятного ...
... актов, направленных на сокращение ядерного вооружения, борьбу с «боевым» терроризмом и его финансированием. 1.2 Преодоление отсталости слаборазвитых стран Другая острейшая глобальная проблема современности заключается в преодолении отсталости в развитии большей части человечества. Отсталость – результат пересечения, теснейшего взаимодействия всех глобальных проблем, и чем глубже мы ...
... ". В соответствии с которой, последние могут представлять собой как раздельные, так и комплексные исследования рынка и маркетинговой деятельности фирмы. Принципиальной особенностью маркетингового исследования, отличающей его от сбора и анализа внутренней и внешней текущей информации, является его целевая направленность на решение определенной проблемы или комплекса проблем маркетинга. Эта ...





0 комментариев