Войти на сайт

Забыли пароль?
Регистрация

Навигация

Главная Рефераты Математика

Метод Ньютона

Итерационные методы решения систем нелинейных уравнений
Метод Ньютона Модификации метода ньютона Другие итерационные методы решения систем нелинейных уравнений Программная реализация итерационных методов Метод градиентного спуска Метод Ньютона Модифицированный метод Ньютона
37732
знака
2
таблицы
12
изображений
Скачать работу
Похожие
Заказать работу
Итерационные методы решения систем нелинейных уравнений Читать далее: Модификации метода ньютона

2.3 Метод Ньютона

Основная идея метода Ньютона состоит в выделении из уравнений линейных частей, которые являются главными при малых приращениях аргументов. Это позволяет свести исходную задачу к решению последовательности линейных систем.

Рассмотрим систему уравнений

 

в предположении, что  – непрерывно-дифференцируемые функции.

Полагая

,

прейдём к векторной записи

 (3.1)

Опишем общий шаг метода. Пусть уже получено приближение  проведём линеаризацию вектор-функции  в окрестности точки  - разложим функцию  в ряд Тейлора, оставив только два первых члена в силу малости отклонения приближения  от корня:


.

Здесь 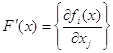– матрица Якоби для вектор-функции .

Очередное приближение  определяется как решение линейной системы , т.е.

Если матрица Якоби  не вырожденна, то решение системы линейной системы можно записать в явном виде, что приводит к стандартной формуле метода Ньютона

 (3.2)

Таким образом, в основе метода Ньютона лежит идея линеаризации вектор-функции  в окрестности каждого приближения (на каждой итерации), что позволяет свести решение системы (3.1) к последовательному решению линейных систем.

Через уже известное приближение  к корню  можно записать, что , где . Тогда после линеаризации получим систему уравнений, линейную относительно . Таким образом, на каждом шаге мы будем находить приращения , и новое приближение к решению по формулам:

 – система линейных уравнений


Рассмотрим вопрос о сходимости метода Ньютона. Точное условие сходимости метода Ньютона для решения систем нелинейных уравнений имеет довольно сложный вид. можно отметить очевидный результат: в достаточно малой окрестности корня итерации сходятся, если матрица Якоби невырожденная, причём сходимость квадратичная.

Приведём ряд теорем, выполнение условий которых должно обеспечивать сходимость метода Ньютона.

Пусть в пространстве  выбрана некоторая векторная норма  и согласованная с ней матричная норма .

Теорема (о сходимости). Пусть

1)                вектор-функция  определена и непрерывно-дифференцируема в области

 

где  – решение уравнения (3.1),

2) для всех  существует обратная матрица , причём

3)для всех

4)

Тогда метод Ньютона (3.2)

1)

2)

3)

Доказательство. Докажем первое утверждение теоремы с помощью индукции. По условию . Допустим, что . Поскольку , то . Рассмотрим условие 3) теоремы для  

.

Согласно формуле (3.2)

,

Кроме того . Тогда предыдущее неравенство принимает вид

Следовательно,

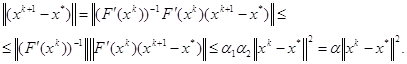
Таким образом, имеет место неравенство

 (3.3)

По предположению индукции . Поскольку в силу условия 4)

, то

Это значит, что для , и шаг индукции реализован. Превое утверждение теоремы доказано.

Продолжим доказательство. Положим перепишем оценку (3.3) после умножения на в виде . Покажем, что

 (3.4)

Будем рассуждать по индукции. При  неравенство (3.4.) очевидно. Допустим, что оно справедливо для некоторого . Тогда

Переход  завершен, т.е. неравенство (3.4) справедливо для всех . Перепишем его в исходных обозначениях

Получили утверждение 3). При этом

, т.е. .

Это значит, что имеет место сходимость:  

Замечание 1. Неравенство (3.3) при условии  означает, что последовательность  сходится к решению  с квадратичной скоростью.

Замечание 2. Поскольку , то из утверждения 3) следует оценка погрешности метода Ньютона

Теорема. Если fi(x) непрерывны, вместе с первыми производными в выпуклой области G, содержащей решение системы $X^{\ast}$и при $x= X^{\ast}$матрица Fx не вырождена, то существует такая окрестность что при любом метод Ньютона сходится к $x^{\ast}$.$\Box$

$x^0\in R$

Доказательство. Рассмотрим

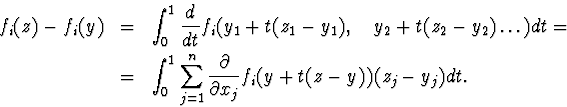
\begin{eqnarray*}f_i(z)-f_i(y)&=&\int^1_0\frac{d}{dt}f_i(y_1+t(z_1-y_1),\quady... ...um^n_{j=1}\frac{\partial}{\partial x_j}f_i(y+t(z-y))(z_j-y_j)dt.\end{eqnarray*}

Введем и матрицу и матрицу. Очевидно, что F(x,x)= F(x), то есть имеем

$F_{ij}(y,z)=\int^1_0\frac{\partial}{\partial x_j}f_i(y+t(z-y))dt$,$F(y,z)=\{F_{ij}\}$
 

 (12)


Есть тождества

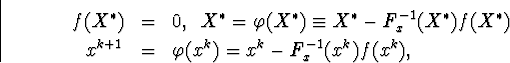
\begin{eqnarray*}f(X^{\ast})&=&0,\enskip X^{\ast}=\varphi(X^{\ast})\equiv X^{\... ...st})f(X^{\ast})\\ x^{k+1}&=&\varphi(x^k)=x^k-F^{-1}_x(x^k)f(x^k),\end{eqnarray*}

Тогда.

\begin{displaymath}x^{k+1}-X^{\ast}=\big[E-F^{-1}_x(x^k)F(X^{\ast},x^k)\big](x^k-X^{\ast}).\end{displaymath}

Вблизи окрестности $X^{\ast}$для любого найдется такое x0, что если,. то

Тогда

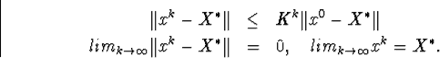
\begin{eqnarray*}\Vert x^k-X^{\ast}\Vert& \leq &K^k\Vert x^0-X^{\ast}\Vert\\ li... ...}\Vert x^k-X^{\ast}\Vert&=&0,\quad lim_{k\to\infty}x^k=X^{\ast}.\end{eqnarray*}

На начальное приближение x0 наложено труднопроверяемое условие.

$\{\Vert x-x^0\Vert\leq\rho\}$Теорема Канторовича. Если функции fi(x) непрерывны вместе со своими 1 -ми и 2 -ми производными в некоторой выпуклой области G, содержащей точку x0 вместе с ее окрестностью и выполнены следующие условия:

в точке x0 существует матрица F-1 такая

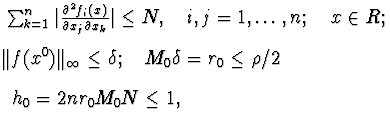
\begin{displaymath}\Vert F^{-1}_x(x^0)\Vert _{\infty}\leq M_0\end{displaymath}

 

то последовательность xk+1=xk-f-1x(xk)F(xk) сходится к $X^{\ast}$.$X^{\ast}$является единственным решением системы f(x)=0 в области и имеет место оценка

\begin{displaymath}\Vert X^{\ast}-x^k\Vert _1\leq(\frac{1}{2})^{k-1}h^{2^k}_0r_0.\end{displaymath}$\Box$

Докажем 3 неравенства

а) $\Vert f(x+\Delta x)-f(x)\Vert _{\infty}\leq F_x(\xi)\Vert\Vert\Delta x\Vert$

б)$\Vert F_x(x+\Delta x)-F_x(x)\Vert\leq nN\Vert\Delta x\Vert$

в) $\Vert f(x+\Delta x)-f(x)-F_x(x)\Delta x\Vert\leq\frac{1}{2}nN\Vert\Delta x\Vert^2_{\infty}$

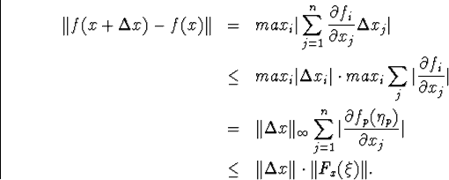
\begin{eqnarray*}\Vert f(x+\Deltax)-f(x)\Vert&=&max_i\vert\sum^n_{j=1} \frac{\... ...ial x_j}\vert\\ &\leq&\Vert\Deltax\Vert\cdot\Vert F_x(\xi)\Vert.\end{eqnarray*}


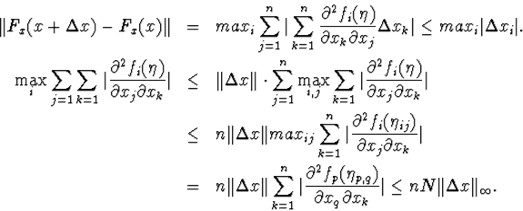
б)\begin{eqnarray*}\Vert F_x(x+\Deltax)-F_x(x)\Vert&=&max_i\sum^n_{j=1}\vert\sum... ...partial x_q\partial x_k}\vert\leq nN\Vert\Deltax\Vert _{\infty}.\end{eqnarray*}

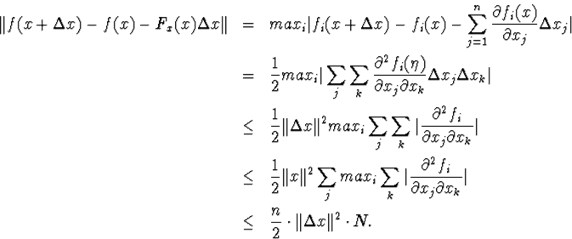
\begin{eqnarray*}\Vert f(x+\Delta x)-f(x)-F_x(x)\Delta x\Vert&=&max_i\vert f_i... ...al x_k}\vert\\ &\leq&\frac{n}{2}\cdot\Vert\Delta x\Vert^2\cdot N.\end{eqnarray*}

в)

\begin{displaymath}\Vert x^1-x^0\Vert=\Vert F^{-1}_x(x^0)f(x^0)\Vert\leq\Vert F^{-1}_x\Vert\Vert f(x^0)\Vert\leqM_0\delta=r_0<\frac{\rho}{2}.\end{displaymath} 

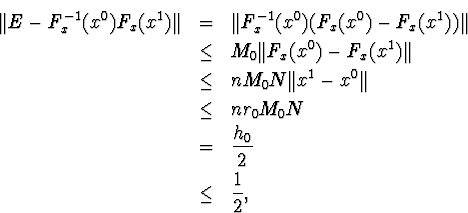
\begin{eqnarray*}\Vert E-F^{-1}_x(x^0)F_x(x^1)\Vert&=&\Vert F^{-1}_x(x^0)(F_x(x... ...0\Vert\\ &\leq&nr_0M_0N\\ &=& \frac{h_0}{2}\\ &\leq&\frac{1}{2},\end{eqnarray*} 

т.е. матрица F-1x(x0)Fx(x1) невырождена, и


\begin{displaymath}\Vert\big[F^{-1}_x(x^0)F_x(x^1)\big]^{-1}\Vert\leq\frac{1}{1-h_0/2}\leq 2.\end{displaymath}

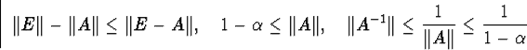
\begin{displaymath}\Vert E\Vert-\Vert A\Vert\leq\Vert E-A\Vert,\quad1-\alpha\l... ...rt A^{-1}\Vert\leq\frac{1}{\Vert A\Vert}\leq\frac{1}{1-\alpha}\end{displaymath}

\begin{displaymath}F^{-1}_x(x^1)=\big[F^{-1}_x(x^0)F_x(x^1)\big]^{-1}F^{-1}_x(x^0)\end{displaymath} и

\begin{displaymath}\Vert F^{-1}_x(x^1)\Vert\leq 2\cdot M_0.\end{displaymath}

Fx(x0)(x1-x0)+f(x0)=0

\begin{displaymath}\Vert f(x^1)\Vert\leq\Vert f(x^1)f(x^0)-F_x(x_0)(x^1-x^0)\Vert\leq\frac{1}{2}nN\cdot r^2_0\end{displaymath}

\begin{displaymath}\Vert F^{-1}(x^1)f(x^1)\Vert\leq\frac{1}{2} nN\cdotr^2_0\cdot 2M_0=(M_0nr_0N)r_0=\frac{h_0r_0}{2}\leq\frac{r_0}{2}.\end{displaymath}

Покажем, что при всех k имеют место неравенства:

 (А)

\begin{displaymath}\Vert F^{-1}_x(x^k)\Vert\leq 2M_0;\quad \Vert f(x^k)\Vert\leq\frac{nNr^2_0}{2^{2k-1}}h^{2^k-2}_0\leq\frac{nNr^2_0}{2^{2k-1}}.\end{displaymath}

\begin{displaymath}\Vert F^{-1}_x(x^k)f(x^k)\Vert\leq\frac{r_0}{2^k} \mbox{, при }k=1\mbox{ ужепоказали.}\end{displaymath}

Пусть имеет место m=k-1

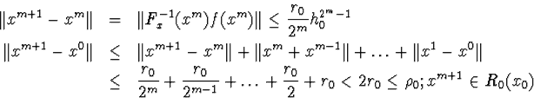
\begin{eqnarray*}\Vert x^{m+1}-x^m\Vert&=&\Vert F^{-1}_x(x^m)f(x^m)\Vert\leq\fr... ...1}}+\ldots+\frac{r_0}{2}+r_0<2r_0\leq\rho_0; x^{m+1}\in R_0(x_0)\end{eqnarray*}

Повторим неравенства

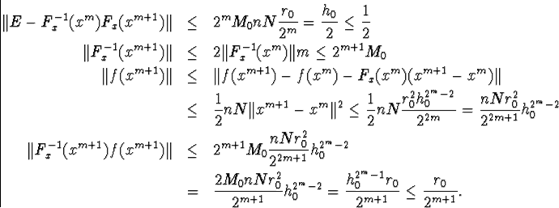
\begin{eqnarray*}\Vert E-F^{-1}_x(x^m)F_x(x^{m+1})\Vert&\leq& 2^mM_0nN\frac{r_0... ...{2^m-2}_0=\frac{h^{2^m-1}_0r_0}{2^{m+1}}\leq\frac{r_0}{2^{m+1}}.\end{eqnarray*}

Неравенство (А) показывает, что в круге R последовательность xk является фундаментальной, т.е. имеется предел.

Оценим сходимость

\begin{eqnarray*}\Vert x^{k+p}-x^k\Vert&\leq&\Vert x^{k+p}-x^{k+p-1}\Vert+\ldot... ...\ldots+\frac{1}{2^{p-1}}\big]\leq\frac{r_0}{2^{k-1}}h^{2^k-1}_0,\end{eqnarray*}т.е.,

устремляя правая часть не меняется,, т.е. при очень хорошая сходимость.


Итерационные методы решения систем нелинейных уравнений Читать далее: Модификации метода ньютона
Информация о работе «Итерационные методы решения систем нелинейных уравнений»
Раздел: Математика
Количество знаков с пробелами: 37732
Количество таблиц: 2
Количество изображений: 12
Скачать

Похожие работы

Решение систем нелинейных уравнений методом Бройдена
Скачать
15003
0
14

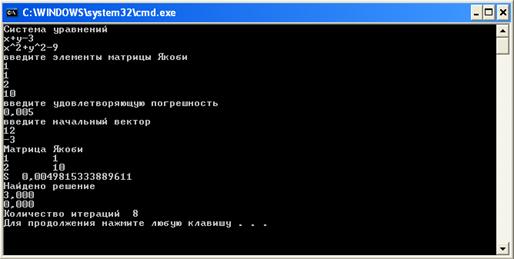
... метод Бройдена, написана программа реализующая его. СПИСОК ЛИТЕРАТУРЫ 1.    С.Л. Подвальный, Л.В. Холопкина. Вычислительная математика- учебное пособие ВГТУ, 2004 - 147 с. 2.    Методы решения систем нелинейных уравнений. Метод Ньютона. Его реализации и модификации. - Электрон. дан. – Режим доступа: www.exponenta.ru/educat/referat/XVkonkurs/15/index.asp. ПРИЛОЖЕНИЕ Текст программы ...

Нахождение корня нелинейного уравнения. Методы решения системы нелинейных уравнений
Скачать
10711
0
8

... –0.6 = 0 9. 10. ( x -1)3 + 0.5ex = 0 11. 12. x5 –3x2 + 1 = 0 13. x3 –4x2 –10x –10 = 0 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. x 4- 2.9x3 +0.1x2 + 5.8x - 4.2=0 25. x4+2.83x3- 4.5x2-64x-20=0 26. МЕТОДЫ РЕШЕНИЯ СИСТЕМЫ НЕЛИНЕЙНЫХ УРАВНЕНИЙ 1.         Постановка задачи Пусть требуется решить систему n ...

Исследование метода простой итерации и метода Ньютона для решения систем двух нелинейных алгебраических уравнений
Скачать
14674
0
13

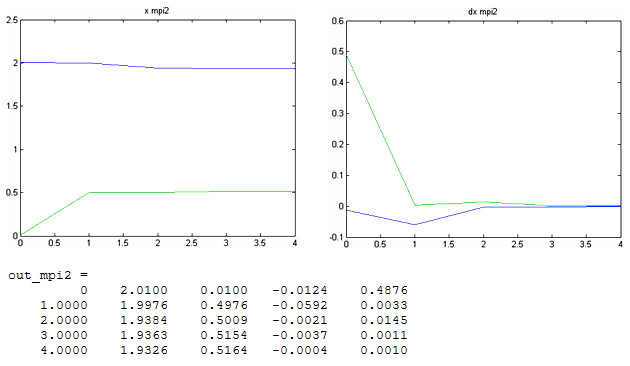
... 1040, мы все еще получаем сходимость, при количестве итераций порядка 130.   4 Анализ результатов, выводы Целью нашего исследование было сравнение методов простой итерации и Ньютона для решения систем из двух нелинейных уравнений по числу итераций, времени сходимости в зависимости от выбора начального приближения к решению и допустимой ошибки. Зависимость этих параметров от выбора начального ...

Экзаменационные билеты по численным методам за первый семестр 2001 года
Скачать
33577
0
0

... с помощью рекурентных соотношений? 104) Приведите конечно-разностные выражения для первой производной. 105) Подынтегральная функция y = f(x) задана таблицейВзяв h = 0,3, вычислить интеграл  на отрезке [0,3; 0,9] методом Симпсона. Зав. кафедрой --------------------------------------------------   Экзаменационный билет по предмету ЧИСЛЕННЫЕ МЕТОДЫ Билет № 22 106) Как ...

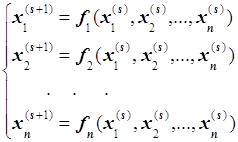
0 комментариев

Разделы
Главная Новости Рефераты Статьи Вузы
Инфо
О проекте Соглашение
Следите за новостями
VK
© 2009-2024 Образовательная социальная сеть KazEdu.com

Наверх