Навигация
Исследование метода простой итерации и метода Ньютона для решения систем двух нелинейных алгебраических уравнений
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»Кафедра экономической информатики
Курсовая работа
по дисциплине «Численные методы»
на тему: «Исследование метода простой итерации и метода Ньютона для решения систем двух нелинейных алгебраических уравнений»
Выполнил
Студент: Обухова Т.С.
Факультет ФБ
Группа ФБИ-72
Преподаватель: Сарычева О.М.
Новосибирск
2009
СОДЕРЖАНИЕ
ВВЕДЕНИЕ
1 Постановка задачи. Математическое описание методов
1.1 Метод простой итерации
1.2 Метод Ньютона
2 Описание программного обеспечения
3 Описание тестовых задач
4 Анализ результатов, выводы
ЗАКЛЮЧЕНИЕ
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
ВВЕДЕНИЕ
Очень часто в различных областях экономики приходится встречаться с математическими задачами, для которых не удается найти решение классическими методами или решения выражены громоздкими формулами, которые не приемлемы для практического использования. Поэтому большое значение приобрели численные методы. В большинстве случаев численные методы являются приближенными, так как с их помощью обычно решаются задачи, аппроксимирующие исходные. В ряде случаев численный метод строится на базе бесконечного процесса, который в пределе сводится к искомому решению. Однако реально предельный переход не удается осуществить, и процесс, прерванный на некотором шаге, дает приближенное решение. Кроме того, источниками погрешности являются несоответствие математической модели изучаемому реальному явлению и погрешность исходных данных.
Решение систем нелинейных алгебраических уравнений – одна из сложных и до конца не решенных задач. Даже о расположении и существовании корней систем нелинейных уравнений почти ничего нельзя сказать. Большинство методов решения систем нелинейных уравнений сходятся к решению, если начальное приближение достаточно близко к нему, и могут вообще не давать решения при произвольном выборе начального приближения. Условия и скорость сходимости каждого итерационного процесса существенно зависят от свойств уравнений, то есть от свойств матрицы системы, и от выбора начальных приближений.
Численный метод, в котором производится последовательное, шаг за шагом, уточнение первоначального грубого приближения решения, называется итерационным. Итерационные методы дают возможность найти решение системы как предел бесконечного вычислительного процесса, позволяющего по уже найденным приближениям к решению построить следующее, более точное приближение. Плюсом таких методов является самоисправляемость и простота реализации на ЭВМ. В точных методах ошибка в вычислениях приводит к накопленной ошибке в результате, а в случае сходящегося итерационного процесса ошибка в каком-либо приближении исправляется в последующих итерациях, и такое исправление требует, как правило, только нескольких лишних шагов единообразных вычислений. Для начала вычислений итерационных методом требуется знание одного или нескольких начальных приближений к решению.
В данной курсовой работе необходимо рассмотреть два из множества существующих итерационных методов - метод простой итерации и метод Ньютона (классический) для решения систем линейных алгебраических уравнений.
1 Постановка задачи. Математическое описание методов
При определенных условиях ЭО в установившемся режиме описывается системой нелинейных АУ вида . Если при этом входной сигнал ![]() известен, то для определения соответствующего значения
известен, то для определения соответствующего значения ![]() необходимо решить систему нелинейных АУ вида:
необходимо решить систему нелинейных АУ вида:
![]() (1)
(1)
Которая в нашем случае представляет собой систему из двух нелинейных уравнений с двумя неизвестными вида:
![]() (2)
(2)
Обобщенный алгоритм решения системы (1) определяется формулой
![]() ,
,
где:
G – вектор-функция размерности n, которая определяется способом построения итерационного процесса;
p – количество предыдущих точек значений X, используемых в данном итерационном процессе.
Если в итерационном процессе используется только одна предыдущая точка (p=1), то
![]()
Рассмотрим подробнее два таких метода – метод простой итерации и метод Ньютона.
1.1 Метод простой итерации
Пусть дана система (2), корни которой требуется найти с заданной точностью.
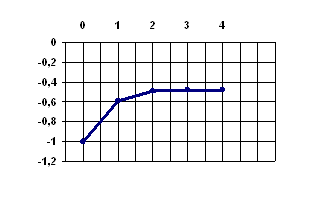
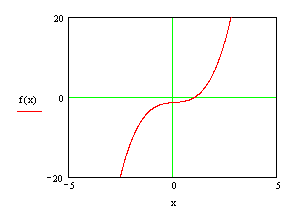
Предположим, что система допускает лишь изолированные корни. Число этих корней и их приближенные значения можно установить, построив кривые ![]() и
и ![]() и определив координаты их точек пересечения (либо из существующих представлений о функционировании экономического объекта).
и определив координаты их точек пересечения (либо из существующих представлений о функционировании экономического объекта).
Для применения метода итераций система (2) приводится к виду
![]() (3)
(3)
Функции ![]() и
и ![]() называются итерирующими. Алгоритм решения задается формулами:
называются итерирующими. Алгоритм решения задается формулами:
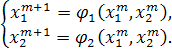 (n=0, 1, 2, …),
(n=0, 1, 2, …),
где ![]() - некоторое начальное приближение.
- некоторое начальное приближение.
Для приведения системы (2) к виду (3) используем следующий прием. Положим
![]() (
(![]() ). (4)
). (4)
Коэффициенты ![]() найдем как приближенные решения следующей системы уравнений:
найдем как приближенные решения следующей системы уравнений:

Характеристики метода:
1. Сходимость.
Локальная, то есть метод сходится при выборе начальных приближений достаточно близко к точному решению. Насколько близко необходимо выбирать начальное приближение, исследуем в практической части.
2. Выбор начального приближения
Начальные значения переменных должны выбираться близко к точным.
3. Скорость сходимости линейная.
4. Критерий окончания итераций.
Определяется по формуле:
![]() ,
,
1.2 Метод Ньютона
Пусть дана система (2). Согласно методу Ньютона последовательные приближения вычисляются по формулам
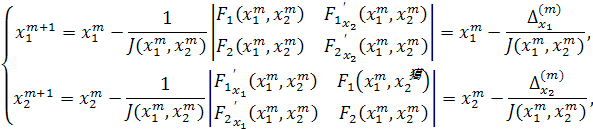
Где
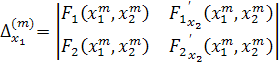 ,
, 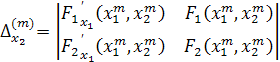 ,
,
а якобиан
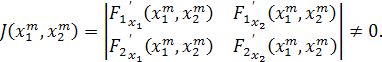
Характеристики метода:
1. Сходимость.
Локальная, то есть метод сходится при выборе начальных приближений достаточно близко к точному решению. Насколько близко необходимо выбирать начальное приближение, исследуем в практической части.
2. Выбор начального приближения
Начальные значения переменных должны выбираться близко к точным.
3. Скорость сходимости квадратичная.
4. Критерий окончания итераций.
Аналогично методу простой итерации:
![]() ,
,
2 Описание программного обеспечения
метод итерация ньютон нелинейное уравнение
Программное обеспечение представлено в виде двух основных модулей – mpi2.m (метод простой итерации) и kmn2.m (классический метод Ньютона) и трех вспомогательных модулей – funF.m (матрица системы), funJ.m (матрица Якоби для системы), head.m (головная программа).
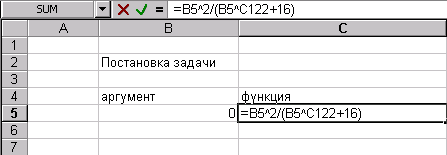
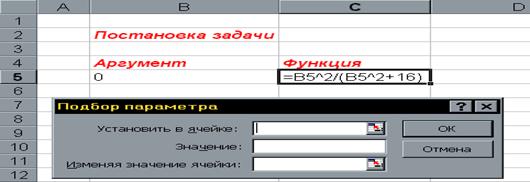
Головная программа – модуль head.m
Используемые переменные:
x0 – вектор начальных приближений;
edop – допустимая ошибка вычислений;
Текст программы:

Исходная система уравнений – модуль funF.m
Входные параметры:
x – вектор - текущее приближение к решению;
Выходные параметры:
F – вектор значений функции, полученных в точке x
Текст программы:
function [F]=funF(x)
F=[![]() ;
; ![]() ];
];
В векторе содержатся функции F1 и F2 по строкам.
Матрица Якоби – модуль funJ.m
Входные параметры:
x – вектор - текущее приближение к решению;
Выходные параметры:
J – матрица Якоби, полученная в точке x
Текст программы:
function[j]=funJ(x)
j=[![]()
![]() ;
;
![]()
![]() ];
];
В матрице содержатся частные производные функций F1 и F2 по x1 и x2.
Метод простой итерации – модуль mpi2.m
Входные параметры:
x0 – вектор начальных приближений;
edop – допустимая ошибка вычислений;
Используемые переменные:
F – вектор функции, полученный в некоторой точке;
J – матрица Якоби, вычисленная от начальных условий;
dx - вектор ошибки на каждом шаге итерационного процесса;
alpha, beta, gamma, delta – параметры используемые для приведения системы (2) к виду (3);
nf, ndx – нормы вектора функции и вектора ошибки соответственно;
x - вектор решения системы на каждом шаге итерационного процесса.
Выходные параметры:
xout – матрица размерности n×2 значений решения системы, составленная по строкам из решений на m-ном шаге;
dxout – матрица размерности n×2 значений ошибки решения, составленная по строкам из ошибок на m-ном шаге;
mout – вектор, составленный из номеров итераций на каждом шаге.
Текст программы:

Классический метод Ньютона – модуль mpi2.m
Входные параметры:
x0 – вектор начальных приближений;
edop – допустимая ошибка вычислений;
Используемые переменные:
F – вектор функции, полученный в некоторой точке;
J – матрица Якоби, вычисленная в некоторой точке;
dx - вектор ошибки на каждом шаге итерационного процесса
delta – вектор промежуточных значений, используемых для расчета dx
nf, ndx – нормы вектора функции и вектора ошибки соответственно;
x - вектор решения системы на каждом шаге итерационного процесса.
Выходные параметры:
xout – матрица размерности n×2 значений решения системы, составленная по строкам из решений на m-ном шаге;
dxout – матрица размерности n×2 значений ошибки решения, составленная по строкам из ошибок на m-ном шаге;
mout – вектор, составленный из номеров итераций на каждом шаге.
Текст программы:

Похожие работы
... точке приближенного решения, т. е. Последовательные приближения (4) строятся по формулам: , (9) где – начальное приближение к точному решению . 4.5 Метод Зейделя на основе линеаризованного уравнения Итерационная формула для построения приближенного решения нелинейного уравнения (2) на основе линеаризованного уравнения (7) имеет вид: 4.6 Метод наискорейшего спуска Методы ...
... . Специалист для которого MS Excel является именно тем средством которое позволяет облегчить и ускорить его работу, должен знать и уметь использовать в повседневной работе новейшие экономико-математические методы и модели, предлагаемые новыми прикладными программами. Традиционный способ изучения экономико-математических методов заключается не только в определении их назначения и сути, ...
... 35437 x4=0.58554 5 x1=1.3179137 x2=-1.59467 x3=0.35371 x4=0.58462 6 x1=1.3181515 x2=-1.59506 x3=0.35455 x4=0.58557 5. Сравнительный анализ различных методов численного дифференцирования и интегрирования 5.1 Методы численного дифференцирования 5.1.1 Описание метода Предположим, что в окрестности точки xiфункция F (x) дифференцируема достаточное число раз. ...
... на языке Turbo Pascal 7.0 для решении систем линейных алгебраических уравнений, используя метод простой итерации. 1.2 Математическая формулировка задачи Пусть А – невырожденная матрица и нужно решить систему где диагональные элементы матрицы А ненулевые. 1.3 Обзор существующих численных методов решения задачи Метод Гаусса В методе Гаусса матрица СЛАУ с помощью равносильных ...
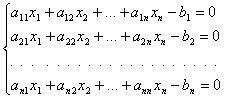
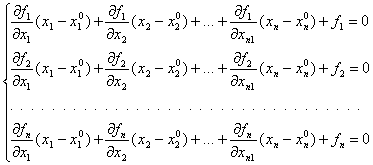
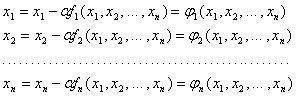
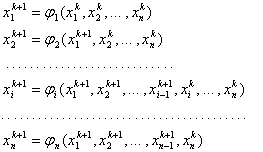
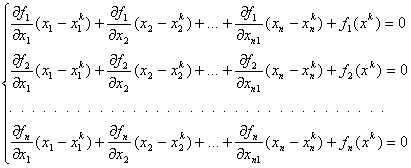


0 комментариев