Навигация
Численные методы решения обыкновенных дифференциальных уравнений
3.1.3.1. Численные методы решения обыкновенных дифференциальных уравнений
3.1.3.1.1. Решение задачи Коши. Дано обыкновенное дифференциальное уравнение первого порядка
![]()
Требуется найти решение ![]() этого уравнения, удовлетворяющее начальному условию
этого уравнения, удовлетворяющее начальному условию ![]() на интервале
на интервале ![]() .
.
Численное решение задачи Коши состоит в нахождении значений ![]() в точках
в точках ![]() отрезка
отрезка ![]() , где
, где ![]() – шаг интегрирования. Число разработанных методов решения задачи Коши очень велико. Можно выделить две группы методов:
– шаг интегрирования. Число разработанных методов решения задачи Коши очень велико. Можно выделить две группы методов:
Одношаговые методы, в которых для нахождения следующей точки на кривой ![]() требуется информация лишь об одном предыдущем шаге.
требуется информация лишь об одном предыдущем шаге.
Одношаговыми являются метод Эйлера и методы Рунге–Кутта.
2. Многошаговые методы (методы прогноза и коррекции), в которых для отыскания следующей точки кривой ![]() требуется информация более чем об одной из предыдущих точек. К числу таких методов относятся методы Милна, Хемминга, Адамса-Башфорта.
требуется информация более чем об одной из предыдущих точек. К числу таких методов относятся методы Милна, Хемминга, Адамса-Башфорта.
3.1.3.1.2. Метод Эйлера. Метод Эйлера – это простейший метод, позволяющий интегрировать дифференциальные уравнения первого порядка. Однако на основе этого метода легче понять алгоритмы других, более эффективных методов.
Метод Эйлера основан на разложении ![]() в ряд Тейлора в окрестности
в ряд Тейлора в окрестности ![]() .
.
Запишем ряд Тейлора:
![]()
При малом ![]() членами высоких порядков можно пренебречь. Тогда:
членами высоких порядков можно пренебречь. Тогда:
![]()
Таким образом, получим значение зависимой переменной ![]() при малом смещении
при малом смещении ![]() от начальной точки
от начальной точки ![]() . Этот процесс можно продолжить, используя соотношение
. Этот процесс можно продолжить, используя соотношение
![]()
или
![]()
3.1.3.1.3. Модифицированный метод Эйлера (метод Эйлера – Коши). Тангенс угла наклона касательной к кривой ![]() известен в
известен в ![]() и равен
и равен ![]() , но он меняется с изменением независимой переменной, и в точке
, но он меняется с изменением независимой переменной, и в точке ![]() наклон касательной уже не такой, как в
наклон касательной уже не такой, как в![]() , т.е. на интервале
, т.е. на интервале ![]() вносится погрешность.
вносится погрешность.
Точность метода Эйлера можно существенно повысить, улучшив аппроксимацию производной. Это можно сделать, использовав среднее значение производной в начале и конце интервала.
В модифицированном методе Эйлера сначала вычисляется значение функции в следующей точке по методу Эйлера.
![]() ,
,
которое используется для приближенного вычисления значения производной в конце интервала, т.е.
![]() .
.
Вычислив среднее значение производной между полученным в начале и в конце интервала, найдем более точное значение ![]() :
:
![]()
Принцип, на котором основан модифицированный метод Эйлера, можно пояснить иначе. Вернемся к разложению в ряд Тейлора:
![]()
Попытаемся сохранить член с ![]() ; для этого
; для этого ![]() аппроксимируем конечной разностью:
аппроксимируем конечной разностью:
![]()
Подставив это выражение в ряд Тейлора, получим:
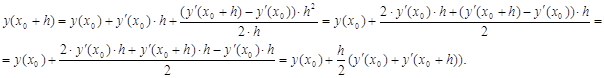
Это выражение совпадает с ранее полученным.
Данный метод является методом второго порядка, поскольку в нем используется член ряда Тейлора, содержащий ![]() .
.
3.1.3.1.4 Метод Рунге – Кутта. Точность одношаговых методов можно повысить, если осуществить более точную аппроксимацию производной на интервале ![]() , т.е. использовать члены более высоких порядков в разложении Тейлора.
, т.е. использовать члены более высоких порядков в разложении Тейлора.
Чтобы удержать в ряде Тейлора член ![]() – го порядка, необходимо вычислять
– го порядка, необходимо вычислять ![]() – ю производную зависимой переменной. При использовании модифицированного метода Эйлера для получения второй производной в конечно – разностной форме достаточно было знать наклоны кривой на концах рассматриваемого интервала. Чтобы вычислить третью производную в конечно– разностном виде, необходимо иметь значения второй производной по меньшей мере в двух точках. Для этого необходимо дополнительно определить наклон кривой в некоторой промежуточной точке интервала
– ю производную зависимой переменной. При использовании модифицированного метода Эйлера для получения второй производной в конечно – разностной форме достаточно было знать наклоны кривой на концах рассматриваемого интервала. Чтобы вычислить третью производную в конечно– разностном виде, необходимо иметь значения второй производной по меньшей мере в двух точках. Для этого необходимо дополнительно определить наклон кривой в некоторой промежуточной точке интервала ![]() , т.е. между
, т.е. между ![]() и
и ![]() . Очевидно, чем выше порядок вычисляемой производной, тем больше дополнительных вычислений потребуется внутри интервала.
. Очевидно, чем выше порядок вычисляемой производной, тем больше дополнительных вычислений потребуется внутри интервала.
Метод Рунге-Кутта дает набор формул для расчета координат внутренних точек, требуемых для реализации этой цели.
Алгоритм Рунге-Кутта первого порядка является методом Эйлера.
Алгоритм Рунге-Кутта второго порядка является модифицированным методом Эйлера (методом Эйлера – Коши). Для вычисления ![]() получаем формулы:
получаем формулы:
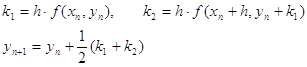
Наиболее распространенный вариант метода – метод четвертого порядка точности. Для вычисления ![]() получаем формулы:
получаем формулы:

3.1.3.1.5 Автоматический выбор шага. В приведенных выше методах величина шага изменения ![]() предполагалась постоянной. Очевидно, что при интегрировании с малой величиной шага мы будем получать более точное решение.
предполагалась постоянной. Очевидно, что при интегрировании с малой величиной шага мы будем получать более точное решение.
Однако, указать заранее приемлемую величину шага сложно. Если шаг выбрать большой, то будет недостаточной точность результатов. Если же шаг выбрать очень малый, то это увеличивает число шагов и время решения.
Поэтому некоторые программы интегрирования, применяемые на практике, снабжены процедурой автоматического выбора шага. В результате этого на участках плавного изменения интегральной кривой шаг автоматически увеличивается, а при резких изменениях функции шаг уменьшается.
3.1.3.1.6. Общая характеристика одношаговых методов. Чтобы получить информацию в новой точке, нужно иметь данные о предыдущей точке.
В основе всех одношаговых методов лежит разложение функции в ряд Тейлора, в котором сохраняются члены, содержащие степени до ![]() включительно. Целое число
включительно. Целое число ![]() называют порядком метода. Погрешность на шаге имеет порядок
называют порядком метода. Погрешность на шаге имеет порядок ![]() .
.
Все одношаговые методы не требуют действительного вычисления производных – вычисляется лишь сама функция (правая часть уравнения). Могут потребоваться значения функции в промежуточных точках, что влечет дополнительные затраты времени.
Похожие работы
уле . Т.о. имеем: Минимальная энергия: Найдем управление по следующей формуле: Тогда оптимальное управление . 3.2 Оптимальная L – проблема моментов в пространстве состояний Система задана в виде: Решение ДУ имеет вид: , при имеем: . Составим моментные уравнения: Подставляя необходимые данные в выше приведенные формулы, получим следующие ...
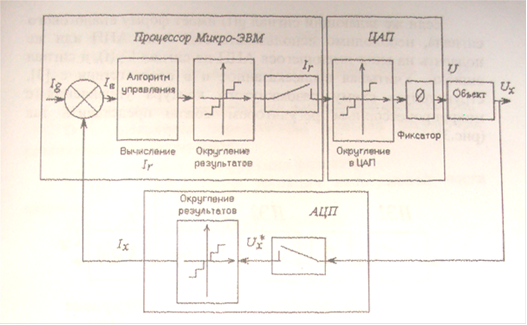
... , Полученные данные будут составлять так называемую неизменяемую часть системы. Получим, что передаточная функция такой неизменяемой части системы имеет вид 2. Структурная схема САУ с микропроцессорным регулятором Поскольку микропроцессорный регулятор построен на базе Микро-ЭВМ и может обрабатывать сигналы только дискретной формы" а сигнал на выходе объекта Ux и регулирующий сигнал Ur - ...
... цепи W1(s) = Wp(s) представлено как параллельное соединение простейших звеньев. 2.9 Неопределенность моделей систем управления Математические модели не отражают исчерпывающим образом динамические свойства систем управления в силу идеализации и упрощений, неизбежных при моделировании, неточной реализации алгоритмов управления и изменений характеристик объектов и других элементов в ...
... , на нерегулируемые его влияние не распространяется. Учет по центрам ответственности позволяет оценить деятельность подразделения и его руководителя, обеспечивает оперативный учет, анализ и контроль, а также предоставление информации о затратах. Задачи анализа затрат на качество обусловливают введение двух отчетных форм: - сводный отчет о затратах на качество, содержащий полную информацию о ...




0 комментариев