Навигация
Получение формулы Ньютона. Определим рекуррентное соотношение для нахождения корня методом Ньютона
2.1.3.3.2. Получение формулы Ньютона. Определим рекуррентное соотношение для нахождения корня методом Ньютона.
Уравнение касательной в точке ![]() можно получить как уравнение прямой, проходящей через заданную точку
можно получить как уравнение прямой, проходящей через заданную точку ![]() и имеющей угловой коэффициент
и имеющей угловой коэффициент ![]() :
:
![]()
В точке ![]() пересечения касательной с осью Х, величина
пересечения касательной с осью Х, величина ![]() равняется нулю:
равняется нулю:
![]()
Отсюда
![]()
В общем случае для вычисления последующего приближения ![]() к корню по известному предыдущему
к корню по известному предыдущему ![]() формула Ньютона имеет вид:
формула Ньютона имеет вид:
![]()
К такому же результату можно придти, используя разложение в ряд Тейлора:
![]()
Члены, содержащие ![]() во второй и более высоких степенях, отбрасываются; используется соотношение
во второй и более высоких степенях, отбрасываются; используется соотношение ![]() . Предполагается, что переход от
. Предполагается, что переход от ![]() к
к ![]() приближает значение функции к нулю так, что
приближает значение функции к нулю так, что ![]() т.е. точка
т.е. точка ![]() выбирается такой, что значение функции в ней равняется нулю:
выбирается такой, что значение функции в ней равняется нулю:
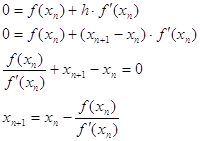
Полученная точка ![]() является точкой пересечения касательной в точке
является точкой пересечения касательной в точке ![]() с осью Х. Поскольку кривая
с осью Х. Поскольку кривая ![]() отлична от прямой, то значение функции
отлична от прямой, то значение функции ![]() скорее всего не будет в точности равно нулю (это результат отбрасывания членов высшего порядка в ряде Тейлора). Поэтому вся процедура повторяется, причем вместо
скорее всего не будет в точности равно нулю (это результат отбрасывания членов высшего порядка в ряде Тейлора). Поэтому вся процедура повторяется, причем вместо ![]() используется
используется ![]() .
.
Одно из преимуществ метода Ньютона – это то, что его можно распространить на решение систем нелинейных уравнений со многими переменными.
2.1.4. Решение систем нелинейных алгебраических и трансцендентных уравнений
2.1.4.1. Постановка задачи. Система n нелинейных уравнений с n неизвестными имеет вид:
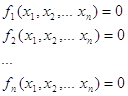 (2.2)
(2.2)
где ![]() – неизвестные;
– неизвестные;
![]() – заданные функции n переменных.
– заданные функции n переменных.
Решением системы НАТУ называется совокупность чисел ![]() , которые, будучи поставлены на место неизвестных
, которые, будучи поставлены на место неизвестных ![]() ,обращают каждое уравнение системы в тождество. Система (2.2) может иметь несколько решений. Нахождение решения системы уравнений является значительно более сложной задачей, чем решение одного уравнения. Для систем НАТУ не существует каких–либо приемов, используя которые получали бы приближенные значения корней. В некоторых случаях в результате построения графиков с последующим определением координат точек пересечения можно получить приближенные значения корней. Для уточнения корней всегда применяются итерационные методы, чаще всего метод Ньютона.
,обращают каждое уравнение системы в тождество. Система (2.2) может иметь несколько решений. Нахождение решения системы уравнений является значительно более сложной задачей, чем решение одного уравнения. Для систем НАТУ не существует каких–либо приемов, используя которые получали бы приближенные значения корней. В некоторых случаях в результате построения графиков с последующим определением координат точек пересечения можно получить приближенные значения корней. Для уточнения корней всегда применяются итерационные методы, чаще всего метод Ньютона.
2.1.4.2. Метод Ньютона для решения систем НАТУ. Представим все n уравнений в виде рядов Тейлора:
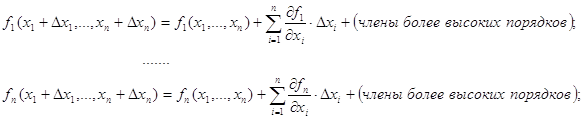 (2.3)
(2.3)
Задача сводится к отысканию такой совокупности приращений ![]() , при которой
, при которой ![]() близки к корню, т.е. левые части уравнений (2.3) обращаются в нули. Отбросив члены более высоких порядков, получим систему линейных алгебраических уравнений (СЛАУ) относительно
близки к корню, т.е. левые части уравнений (2.3) обращаются в нули. Отбросив члены более высоких порядков, получим систему линейных алгебраических уравнений (СЛАУ) относительно ![]() :
:
 (2.4)
(2.4)
Систему линейных уравнений (5.4) можно записать в матричном виде:
 (2.5),
(2.5),
где матрица коэффициентов (А) состоит из частных производных функций по всем переменным, а вектор свободных членов (В) – из функций с противоположным знаком. Матрица в левой части (2.5) называется матрицей Якоби или якобианом.
Найденные из системы (2.5) значения ![]() используются как поправки для получения очередного
используются как поправки для получения очередного ![]() – го приближения к решению:
– го приближения к решению:
 (2.6)
(2.6)
Таким образом, для выполнения одной итерации методом Ньютона решают СЛАУ (2.5) относительно вектора поправок ![]() . Получив значение вектора поправок
. Получив значение вектора поправок ![]() (
(![]() ), получим очередное приближение к корням
), получим очередное приближение к корням ![]() (
(![]() ) (2.6) и т.д. до тех пор, пока все получаемые поправки
) (2.6) и т.д. до тех пор, пока все получаемые поправки ![]() не будут достаточно малы, что свидетельствует о близости приближенного решения к истинному
не будут достаточно малы, что свидетельствует о близости приближенного решения к истинному ![]() (
(![]() ).
).
Следует обратить внимание на то, что проверку поправок ![]() на каждом шаге итерации на условие
на каждом шаге итерации на условие ![]() <
<![]() (
(![]() ) необходимо выполнять для значений поправок всех корней (
) необходимо выполнять для значений поправок всех корней (![]() .
.
Пример: Найти методом Ньютона решение системы уравнений
![]()

Решение. Очевидно, 
Для формирования матрицы Якоби получим частные производные:
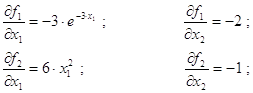
Подставив в (2.5) в качестве: матрицы коэффициентов (А) – частные производные функций и вектора свободных членов (В) – функции с противоположным знаком, получим запись СЛАУ в виде:
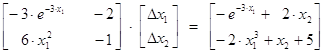 (2.7)
(2.7)
Задавшись некоторым начальным приближением ![]() (
(![]() ) и, подставив его вместо
) и, подставив его вместо ![]() (
(![]() ) в систему (2.7), решим полученную систему линейных уравнений (например, матричным способом
) в систему (2.7), решим полученную систему линейных уравнений (например, матричным способом ![]() ) и получим значение поправок
) и получим значение поправок ![]() . Если поправки не будут достаточно малы (т.е. условие
. Если поправки не будут достаточно малы (т.е. условие ![]() <
<![]() не выполняется), то вычисляется очередное приближение к корням:
не выполняется), то вычисляется очередное приближение к корням: 
С полученным ![]() затем повторяют те же операции, что и с
затем повторяют те же операции, что и с ![]() для получения
для получения ![]() и, если необходимо,
и, если необходимо, ![]() и т.д. до тех пор, пока все получаемые поправки
и т.д. до тех пор, пока все получаемые поправки ![]() не будут достаточно малы, что свидетельствует о близости приближенного решения к истинному.
не будут достаточно малы, что свидетельствует о близости приближенного решения к истинному.
Похожие работы
уле . Т.о. имеем: Минимальная энергия: Найдем управление по следующей формуле: Тогда оптимальное управление . 3.2 Оптимальная L – проблема моментов в пространстве состояний Система задана в виде: Решение ДУ имеет вид: , при имеем: . Составим моментные уравнения: Подставляя необходимые данные в выше приведенные формулы, получим следующие ...
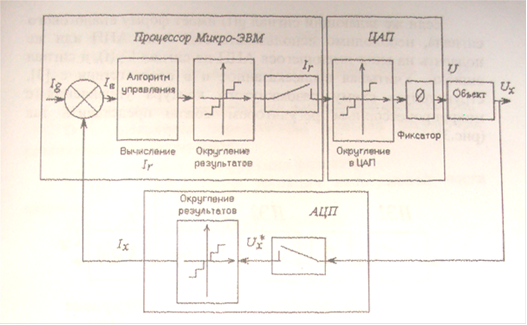
... , Полученные данные будут составлять так называемую неизменяемую часть системы. Получим, что передаточная функция такой неизменяемой части системы имеет вид 2. Структурная схема САУ с микропроцессорным регулятором Поскольку микропроцессорный регулятор построен на базе Микро-ЭВМ и может обрабатывать сигналы только дискретной формы" а сигнал на выходе объекта Ux и регулирующий сигнал Ur - ...
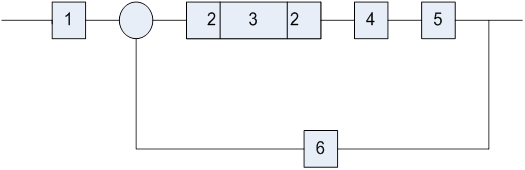
... цепи W1(s) = Wp(s) представлено как параллельное соединение простейших звеньев. 2.9 Неопределенность моделей систем управления Математические модели не отражают исчерпывающим образом динамические свойства систем управления в силу идеализации и упрощений, неизбежных при моделировании, неточной реализации алгоритмов управления и изменений характеристик объектов и других элементов в ...
... , на нерегулируемые его влияние не распространяется. Учет по центрам ответственности позволяет оценить деятельность подразделения и его руководителя, обеспечивает оперативный учет, анализ и контроль, а также предоставление информации о затратах. Задачи анализа затрат на качество обусловливают введение двух отчетных форм: - сводный отчет о затратах на качество, содержащий полную информацию о ...




0 комментариев