Навигация
Тезис (главная цель доказательства - установить истинность тезиса). Форма выражения тезиса - суждение
1. Тезис (главная цель доказательства - установить истинность тезиса). Форма выражения тезиса - суждение.
2. Аргументы (основания) доказательства - положения, на которые опирается доказательство и из которых при условии их истинности необходимо следует истинность доказываемого тезиса. Форма выражения аргументов - суждения. Связывая аргументы, приходим к умозаключению, которые строятся по определенным правилам. Аргументы, на которые можно опереться при доказательстве: аксиомы, определения, ранее доказанные теоремы.
3. Демонстрация - логический процесс взаимосвязи суждений, в результате которого осуществляется переход от аргументов к тезису.
Известно, что имея некоторую (прямую) теорему (P => G), можно образовать новые теоремы, и не одну:
G => P - обратная;
__
P => G - противоположная;
__
G => P - контрапозитивная (обратная противоположной или противоположнообратная).
Между этими четырьмя видами теорем существует тесная связь:
__
а) (P =>G) и (G => P) - одновременно истинны или ложны;
__
б) (G =>P) и (P => G) - одновременно истинны или ложны.
Изучая какую-либо теорему школьного курса математики, учитель должен придерживаться следующей последовательности:
1. Постановка вопроса (создание проблемной ситуации).
2. Обращение к опыту учащихся.
3. Высказывание предположения.
4. Поиск возможных путей решения.
5. Доказательство найденного факта.
6. Проведение доказательства в максимально простой форме.
7. Установление зависимости доказанной теоремы от ранее известных.
Процесс изучения школьниками теоремы включает следующие этапы: мотивация изучения теоремы; ознакомление с фактом, отраженным в теореме; формулировка теоремы и выяснение смысла каждого слова в формулировке теоремы; усвоение содержания теоремы; запоминание формулировки теоремы; ознакомление со способом доказательства; доказательство теоремы; применение теоремы; установление связей теоремы с ранее изученными теоремами.
При доказательстве математических утверждений используются разные абстрактно-дедуктивные математические методы.
Для того, чтобы учащиеся овладели прямым и косвенным доказательствами, необходимо сформировать у них определенную последовательность умений:
- умение искать доказательство,
- умение проводить доказательство,
- умение оформлять доказательство теоремы.
Функции и графикиПусть даны две переменные х и у. Говорят, что переменная у является функцией от переменной х, если задана такая зависимость между этими переменными, которая позволяет для каждого, значения х однозначно определить значение у.
Примеры функций:
1. y = kx+b.
2. у= |х|.
3. у = х2.
4. у= 1/х, х>0
5. у = √х.
В каждом из этих примеров указана формула, позволяющая для каждого значения переменной х однозначно вычислить значение переменной у.
Для того чтобы задать функцию, нужно:
1) указать множество всех возможных значений переменной х. Это множество, которое мы будем обозначать D, называют областью определения функции;
2) указать правило, по которому каждому числу х из множества D сопоставляется число у, определяемое числом х. Это число у называется значением функции в точке х. Переменную х называют аргументом.
Функция обычно обозначается одной буквой, например f. Значение функции f в точке х обозначается f (х).
Итак, если задана функция f, то задано множество чисел D и каждому числу x![]() D сопоставлено число y = f(x).
D сопоставлено число y = f(x).
Пусть задана функция f. с областью определения D. Рассмотрим координатную плоскость. По оси абсцисс будем откладывать значение аргумента, а по оси ординат — значение функции. Для каждого числа x![]() D можно вычислить y = f(x) и построить точку М (х; f (х)). Множество всех таких точек образует кривую, называемую графиком функции / в заданной системе координат.
D можно вычислить y = f(x) и построить точку М (х; f (х)). Множество всех таких точек образует кривую, называемую графиком функции / в заданной системе координат.
Итак, графиком функции f называется множество точек плоскости с координатами (х; f(х)), где х пробегает область определения функции f.
На рисунке 2 изображены графики функций, которые были приведены в качестве примера в начале параграфа.
Рассмотренные нами ранее простейшие зависимости определяют три важнейшие функции:
![]()
Эти функции являются стандартными примерами функций из трех классов, с которыми мы будем часто сталкиваться в дальнейшем: линейных, дробно-линейных и квадратичных.
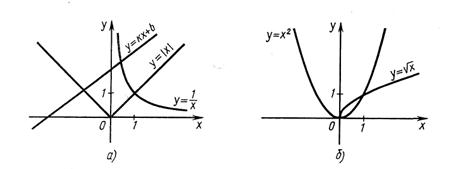
Рис. 2
Для того чтобы определить переменную у как функцию от переменной х, нужно задать множество значений аргумента х и указать правило вычисления значений у в зависимости от х. Сначала обсудим, как задается правило вычисления значений. Во всех приведенных ранее примерах правило вычисления задавалось формулой, содержащей определенные операции.
Обучаясь математике, мы знакомились с различными действиями, операциями над числами. Например, используя только сложение и умножение, мы можем из числа х получить новые числа, скажем 3х, 3х + 5, х3 + 3х + 5 и т. д. Уже такого рода выражения, многочлены, могут служить для построения довольно богатого запаса функций.
Использование деления сильно расширяет этот запас, позволяет образовать выражения вида![]() и т. п. Функции, которые строятся как отношения многочленов, называют рациональными.
и т. п. Функции, которые строятся как отношения многочленов, называют рациональными.
Операция деления отличается от сложения и умножения тем, что она не всегда определена — в знаменателе дроби нельзя ставить нуль. Поэтому, например, в выражение ![]() можно подставить любые числа, кроме х=1 и х=-1, при которых знаменатель равен нулю.
можно подставить любые числа, кроме х=1 и х=-1, при которых знаменатель равен нулю.
Появление новых операций и введение специальных знаков для их обозначения приводят к дальнейшему обогащению наших возможностей — извлечение корня, переход к модулю числа и т. п.
Например, пусть f (х) равно числу —1, если х<0, равно нулю, если х = 0, и равно 1, если х>0. Этими словами мы описали некоторое правило вычисления, применимое к любому числу. Обозначим число f (х), найденное по этому правилу, через sgn х (от латинского слова signum, что означает «знак»). Теперь мы с помощью символа для обозначения новой операции можем строить новые формулы, например ![]()
Если функция задана формулой и не указано никаких ограничений, ее областью определения считается множество всех значений аргумента, при которых выполнимы все операции, участвующие в этой формуле. Это множество называют естественной областью определения данной функции.
Так, естественной областью определения функции ![]() является множество чисел х, для которых
является множество чисел х, для которых ![]() , т. е. промежуток [— 1; 1].
, т. е. промежуток [— 1; 1].
Еще раз обратим внимание на то, что две важные операции — деление и извлечение корня четной степени — выполнимы не всегда (нельзя разделить на нуль, нельзя извлечь корень четной степени из отрицательного числа). Это ограничение надо помнить и учитывать при нахождении области определения функции, в задании которой участвуют указанные операции.
Значения функции ![]() вычисляются путем последовательного выполнения операций: возведение в квадрат, прибавление единицы, извлечение квадратного корня. Можно сказать, что функция
вычисляются путем последовательного выполнения операций: возведение в квадрат, прибавление единицы, извлечение квадратного корня. Можно сказать, что функция ![]() является «сложной функцией», составленной из более простых: и=х2, u = u+l, у=√u.
является «сложной функцией», составленной из более простых: и=х2, u = u+l, у=√u.
Итак, правила вычисления значений функции могут задаваться формулами, полученными с помощью известных нам ранее действий над числами.
Другой важный способ задания функции — табличный. В таблице можно непосредственно указать значения функции, однако лишь для конечного набора значений аргумента.
Вычисление значений функции может быть запрограммировано в калькуляторе. Вычислительное устройство может служить для вас способом задания новой функции. Современные вычислительные машины снабжены клавишами, позволяющими немедленно вычислить значения многих полезных функций.
Наконец, часто функцию задают с помощью графика. Графический способ задания функции очень удобен: он дает возможность наглядно представить свойства функции. Приведем примеры.
На рисунке 3 изображены вольтамперные характеристики некоторых электрических элементов, т.е. графически заданные зависимости напряжения от силы тока. Они получены не по готовой формуле, а экспериментально.
На рисунке 4 изображена кардиограмма работы человеческого сердца. Ее можно считать графиком изменения электрического потенциала на волокнах сердечной мышцы во время сердечного цикла.

Рассмотрим функцию y = f(x), график которой изображен на схеме II. Что можно сказать о свойствах функции f, глядя на график?
1) Спроектируем точки графика на ось х. Мы получим отрезок [а; б]. Этот промежуток является областью определения функции. Действительно, каждая прямая, параллельная оси у, проходящая через точку этого отрезка, пересекает график ровно в одной точке; вертикальные прямые, проходящие через точки х вне отрезка [а; б], график не пересекают.
2) Рассмотрим точки пересечения графика с осью х. На чертеже это х1, х2, х3, х4. В этих точках функция обращается в нуль. Числа х1, х2, х3, х4.являются решениями уравнения f(x) = 0 и называются корнями функции (или ее нулями).
3) Корни функции f разбивают область определения на промежутки, в каждом из которых функция сохраняет постоянный знак. Функция положительна на промежутках [а;х1), (х1;х2), (х4;b] и отрицательна на промежутках (х1;х2), (х3;х4).
Объединение промежутков представляет [а;х1), (х2;х3), и (х4;b] собой решение неравенства f (х) > 0, а объединение промежутков (х1; х2) и (х3;х4).— решение неравенства f(x)<0.
4) График функции можно сравнить с профилем дороги, которая то поднимается в гору, то опускается в ложбину. Самые верхние и самые нижние точки этой дороги («вершины») играют важную роль при описании графика. Они соответствуют значениям аргумента, обозначенным на графике т1, т2, т3.
Производная и ее применениеЧасто нас интересует не значение какой-либо величины, а ее изменение. Например, сила упругости пружины пропорциональна удлинению пружины; работа есть изменение энергии; средняя скорость — это отношение перемещения к промежутку времени, за который было совершено это перемещение, и т. д.
При сравнении значения функции f в некоторой фиксированной точке х0 со значениями этой функции в различных точках х, лежащих в окрестности х0, удобно выражать разность f (х) — f (х0) через разность х — х0, пользуясь понятиями «приращение аргумента» и «приращение функции». Объясним их смысл.
Пусть х — произвольная точка, лежащая в некоторой окрестности фиксированной точки х0. Разность х — х0 называется приращением независимой переменной (или приращением аргумента) в точке х0 и обозначается ∆х;. Таким образом,
∆х=х-х0,
откуда следует, что х=х0+∆х
Говорят также, что Первоначальное значение аргумента х0 получило приращение ∆х. Вследствие этого значение функции f изменится на величину
f(x) – f(x0) = f(x0+∆х) – f(x0)
Эта разность называется приращением функции f в точке х0, соответствующим приращению ∆х, и обозначается символом ∆f (читается «дельта эф»), т. е. по определению
∆f = f(x0+∆х) – f(x0)
откуда
f(x) = f(x0+∆х) = f(x0) ∆f
Обратите внимание: при фиксированном x0 приращение ∆f есть функция от ∆х.
∆f называют также приращением зависимой переменной и обозначают через ∆у для функции y = f(x).
Пример: Дан куб с ребром а. Выразим погрешность ∆V, допущенную при вычислении объема этого куба, если погрешность при измерении длины ребра равна ∆х. По определению приращения х = a + ∆x, тогда
![]()
Рассмотрим график функции y = f(x). Геометрический смысл приращений ∆х и ∆f (приращение ∆f обозначают также ∆у) можно понять, рассмотрев рисунок 80.
Прямую l, проходящую через любые две точки графика функции l, называют секущей к графику f. Угловой коэффициент k секущей, проходящей через точки (х0; y0) и (х; у), равен ![]() .
.
Его удобно выразить через приращения ∆х и ∆у.
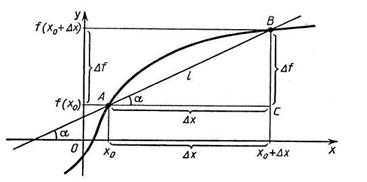
(Напомним, что угловой коэффициент прямой y = kx+b равен тангенсу угла а, который эта прямая образует с осью абсцисс.)
С помощью введенных обозначений приращений удобно также выражать среднюю скорость движения за промежуток времени [t0;t0+∆t]. Если точка движется по прямой и известна ее координата х(t), то
![]()
Эта формула верна и для ∆t<0 (для промежутка [t0 + ∆t; t0]). В самом деле, в этом случае перемещение точки равно х (t0) — x(t0 + ∆x); длительность промежутка времени равна —∆t, и, следовательно,
![]()
Аналогично выражение ![]() называют средней скоростью изменения функции на промежутке с концами x0 и x0+∆х.
называют средней скоростью изменения функции на промежутке с концами x0 и x0+∆х.
Вспомним пример из механики. Если в начальный момент времени t = 0 скорость тела равна 0, т. е. u (0) = 0, то при свободном падении тело к моменту времени t пройдет путь
![]() (1)
(1)
Формула (1) была найдена Галилеем экспериментально. Дифференцированием находим скорость:
![]() (2)
(2)
Второе дифференцирование дает ускорение:
![]()
т. е. ускорение постоянно.
Более типично для механики иное положение: известно ускорение точки a(t) (в нашем случае оно постоянно), требуется найти закон изменения скорости u (t), а также найти координату s (t). Иными словами, по заданной производной u′(t), равной a (t), надо найти u (t), а затем по производной s′(t), равной u (t), найти s (t).
Для решения таких задач служит операция интегрирования, обратная операции дифференцирования.
Определение. Функция F называется первообразной для функции f на заданном промежутке, если для всех х из этого промежутка
F'(x)=f(x).
Показательная и логарифмическая функции
1. Определение корня. С понятием квадратного корня из числа, а вы уже знакомы: это такое число, квадрат которого равен а. Аналогично определяется корень п-й степени из числа а, где п — произвольное натуральное число.
Определение. Корнем п-й степени из числа а называется такое число, п-я степень которого равна а.
Пример 1. Корень третьей степени из числа 27 равен 3, так как З3 = 27. Числа 2 и - 2 являются корнями шестой степени из числа 64, поскольку 26 = 64 и (- 2)6 = 64.
Согласно данному определению корень п-я степени из числа а — это решение уравнения хп = а. Число корней этого уравнения зависит от п и а. Рассмотрим функцию f (х) = хп. Как известно, на промежутке [0; ∞) эта функция при любом п возрастает и принимает все значения из промежутка [0; ∞). По теореме о корне уравнение хп = а для любого а![]() [0; оо) имеет неотрицательный корень и притом только один. Его называют арифметическим корнем п-й степени из числа an обозначают
[0; оо) имеет неотрицательный корень и притом только один. Его называют арифметическим корнем п-й степени из числа an обозначают ![]() ; число п называется показателем корня, а само число а — подкоренным выражением. Знак корня √ называют также радикалом.
; число п называется показателем корня, а само число а — подкоренным выражением. Знак корня √ называют также радикалом.
Определение. Арифметическим корнем п-й степени из числа а называют неотрицательное число, п-я степень которого равна а.
При четных п функция f(x) = xn четна. Отсюда следует, что если а>0, то уравнение хп = а, кроме корня х1 = ![]() , имеет также корень х2 = -
, имеет также корень х2 = - ![]() ,. Если а = 0, то корень один: х = 0; если а<0, то это уравнение корней не имеет, поскольку четная степень любого числа неотрицательна.
,. Если а = 0, то корень один: х = 0; если а<0, то это уравнение корней не имеет, поскольку четная степень любого числа неотрицательна.
Итак, при четном п существуют два корня п-й степени из любого положительного числа а; корень п-й степени из числа 0 равен нулю; корней -четной степени из отрицательных чисел не существует.
При нечетных значениях п функция f(x) = xn возрастает на всей числовой прямой; ее область значений — множество всех действительных чисел. Применяя теорему о корне, находим, что уравнение хп — а имеет один корень при любом а и, в частности, при а<0. Этот корень для любого значения а (в том числе и а отрицательного) обозначают ![]()
Итак, при нечетном п существует корень п-й степени из любого числа а и притом только один.
Для корней нечетной степени справедливо равенство
![]()
В самом деле,
![]()
т.е. число —![]() есть корень n-й степени из — а. Но такой корень при нечетном п единственный. Следовательно,
есть корень n-й степени из — а. Но такой корень при нечетном п единственный. Следовательно, ![]()
Равенство ![]() (при нечетном п) позволяет выразить корень нечетной степени из отрицательного числа через арифметический корень той же степени. Например,
(при нечетном п) позволяет выразить корень нечетной степени из отрицательного числа через арифметический корень той же степени. Например,![]() .
.
Замечание. Для любого действительного х
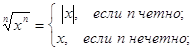
Замечание. Удобно считать, что корень первой степени из числа а равен а. Как вы уже знаете, корень второй степени из числа называют квадратным корнем, а показатель 2 корня при записи опускают (например, корень квадратный из 7 обозначают просто ![]() ) Корень третьей степени называют кубическим корнем.
) Корень третьей степени называют кубическим корнем.
2. Основные свойства корней. Напомним известные вам свойства арифметических корней л-й степени.
Для любого натурального п, целого k и любых неотрицательных чисел а и b выполнены равенства:

Докажем свойство 10. По определению ![]() — это такое неотрицательное число, п-я степень которого равна ab. Число
— это такое неотрицательное число, п-я степень которого равна ab. Число ![]() ·
·![]() неотрицательно. Поэтому достаточно проверить справедливость равенства (
неотрицательно. Поэтому достаточно проверить справедливость равенства (![]() ·
·![]() )п=ab которое вытекает из свойств степени с натуральным показателем и определения корня n-й степени: (
)п=ab которое вытекает из свойств степени с натуральным показателем и определения корня n-й степени: (![]() ·
·![]() )п=(
)п=(![]() )n(
)n(![]() )n=ab
)n=ab
Аналогично доказываются следующие три свойства:

Докажем теперь свойство 50. Заметим, что n-я степень числа (![]() )k равна ak:
)k равна ak:
![]()
По определению арифметического корня (![]() )k=
)k=![]() k (так как
k (так как ![]() ).
).
Похожие работы
... Z целых чисел можно записать на языке свойств в виде Z N или N или =0, где N - множество чисел, противоположных натуральным. 4. Характеристика основных этапов изучения математических понятий Методика работы над определением предполагает: 1) знание определения; 2) обучение распознавания объекта, соответствующего данному определению; 3) построение различных контрпримеров. Например, понятие ...
х средств усвоения курса математики в средней школе. Осуществление преемственности между обучением в начальных классах и в средней школе очень важно. Уже в младших классах надо проводить определенную работу по формированию умения строить правильные дедуктивные умозаключения. В процессе обучения дедуктивным умозаключениям, обращаясь к наблюдению, сравнению, то есть доступным для них операциям, ...
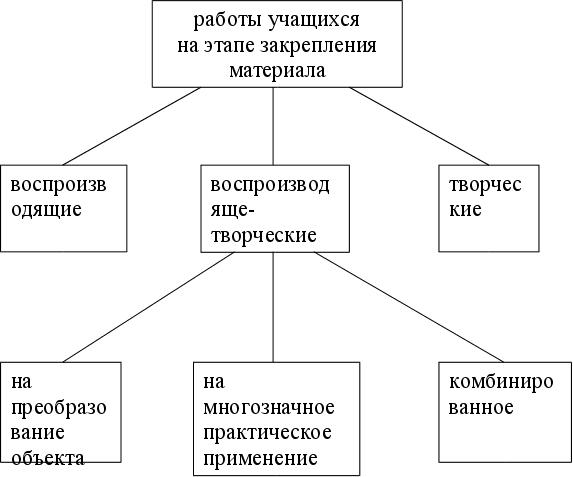
... , творческая познавательная деятельность учащихся всё более и более сближается с научно-исследовательской работой. Глава II. Пути формирования познавательного интереса младших школьников на уроках русского языка через использование творческих заданий§ 1. Воспроизводящие и творческие работы учащихся на отдельных этапах учебного процесса на уроках русского языка В практике обучения русскому ...
... дроби, использовать знания по оперированию единицами величины, при решении задач. развивающие: развивать логическое мышление, память, внимание, умение оперировать обыкновенными дробями. воспитательные: воспитывать любовь к математике, дисциплинированность, самостоятельность, аккуратность. Ход урока. I. Организация класса - Здравствуйте, ребята! Приготовитесь к уроку. ...
0 комментариев