Этап. Постановка (формулировка) задачи (проблемы)

1 этап. Постановка (формулировка) задачи (проблемы).

На этом этапе аналитик должен трансформировать слова заказчика "хочу, чтобы было так" в четко сформулированную задачу. В 99% случаях заказчик не только не может предоставить, но и понятия не имеет о тех данных, которые необходимы аналитику для успешного разрешения проблемы. Оно и понятно – ведь у него нет соответствующего образования. (На самом деле, такое образование заказчику и не нужно, ведь он обратился к грамотному специалисту-аналитику, выпускнику ЗГИА! J) Все необходимое аналитик должен добыть себе сам. Так будет лучше по всем показателям – и по времени и, что немаловажно, по искажению информации (формулировка задачи с чьих-то слов уже априори чревато ошибками). Аналитику необходимо увидеть и изучить проблему "изнутри", для этого ему нужно "внедриться" в сложившуюся ситуацию. Зачастую аналитику надо "внедриться" и поработать на всех ключевых постах в организации заказчика, столкнувшейся с проблемой. На это может уйти от нескольких дней до месяцев.

2 этап. Построение математической модели задачи.

Здесь четко поставленная и сформулированная жизненная проблема формализуется математически.

1)  Определяются переменные – переменные величины (их может быть как несколько, так и одна), изменение которых влияет на конечный результат задачи. Наборы различных конкретных значений переменных называются альтернативами (также во многих литературных источниках набор переменных называется планом).

2)  Определяются ограничения, которые накладываются на переменные. Пересечение всех полученных ограничений задает допустимое множество. Набор переменных, которые удовлетворяют всем ограничениям, называется допустимым планом.

3)  Определяется критерий, по которому должны отбираться альтернативные решения (планы). Такой критерий называется целевой функцией.

Задача состоит в том, чтобы найти такой набор переменных (выбрать такую альтернативу), чтобы они принадлежали допустимому множеству (т.е. удовлетворяли всем ограничениям задачи) и чтобы целевая функция от этих переменных принимала свое оптимальное значение. Такой набор переменных называется оптимальным планом. Понятно, что оптимальный план должен быть допустимым, поэтому и ищется оптимальный план только среди допустимых планов.

Описанными первыми двумя этапами занимается дисциплина "математическое моделирование", являющаяся составной частью исследования операций.

3 этап. Решение математической модели задачи.

Решением математических моделей задач занимается дисциплина "математическое программирование".

В исследовании операций нет единого общего метода решений всех математических моделей. Многолетние исследования позволили обобщить и сгруппировать схожие типы моделей в определенные классы задач. Методы решения данных классов задач составляют отдельные разделы математического программирования, со временем они даже трансформировались в отдельные дисциплины. Дадим краткий обзор некоторых из них.

1) Линейное программирование. В этом классе задач и целевая функция и все ограничения являются линейными функциями. К таким задачам относятся:

задача о плане производства;

задача о диете;

и др.

2) Целочисленное программирование. В этих задачах целевая функция и все ограничения также являются линейными. Все переменные должны принимать только целочисленные значения. К таким задачам относятся:

транспортная задача;

задача о назначениях;

и др.

3) Динамическое программирование. Применяется, когда исходную задачу можно разбить на меньшие подзадачи и решать их пошагово. К таким задачам относятся:

задача коммивояжера;

задача об управлении запасами;

задача о ранце;

и др.

4) Нелинейное программирование. В этом классе задач либо целевая функция, либо все или некоторые ограничения являются нелинейными функциями.

Еще раз акцентируем внимание, что выше приведены лишь некоторые основные разделы математического программирования. Кроме указанных разделов еще существуют теория графов, теория расписаний, сетевое планирование, системы массового обслуживания, теория марковских процессов и др. Каждый раздел математического программирования – это отдельная сформировавшаяся дисциплина, требующая достаточно углубленного теоретического и, особенно, практического изучения.

4 этап. Принятие решений.

На этой стадии аналитик (лицо, принимающее решение) на основе пройденных предыдущих этапов должен принять оптимальное решение. Это и является предметом изучаемого курса "Теория принятия решений".

Само собой разумеется, что студенты, приступившие к изучению курса "Теория принятия решений" ранее должны были изучить и, что немаловажно, успешно сдать и математическое моделирование, и математическое программирование. Без этого необходимого условия ЛПР вряд ли примет оптимальное решение. Невозможно ведь учиться в пятом классе, до этого не выучив во втором классе таблицы умножения! Равно как и невозможно быть директором роддома, не зная, откуда берутся дети.

Принятие решения – это задача управленческого типа. Под ней понимается задача выбора лицом, принимающим решение (ЛПР) наилучшего способа (исхода) из некоторого конечного множества допустимых вариантов (альтернатив). После принятия решения изучаемая система переходит в новое состояние, на которое будет реагировать окружающая среда. Окружающей средой может быть военная, экономическая, финансовая, техническая или какая-либо другая обстановка. При этом возможны такие случаи:

1)  ЛПР знает реакцию окружающей среды на выбор им той или иной альтернативы, т.е. он знает насколько "полезной" или "вредной" для его системы будет реакция окружающей среды на выбор им той или иной альтернативы. Такая ситуация называется задачей принятия решения в условиях определенности. В условиях определенности математическое программирование дает точное решение поставленной задачи. Поэтому необходимости выбирать из нескольких вариантов попросту нет. Таким образом, в условиях определенности "Теория принятия решений" не используется, такими задачами занимается математическое программирование.

2)  ЛПР знает вероятность реакции окружающей среды на выбор им той или иной альтернативы. Такая ситуация называется задачей принятия решения в условиях риска.

3)  ЛПР ничего не знает о реакции окружающей среды на выбор им той или иной альтернативы. Такая ситуация называется задачей принятия решения в условиях неопределенности.

При этом предполагается, что в перечисленных случаях окружающая среда реагирует на принятое ЛПР решение беспристрастно (как природа), не преследуя никаких своих целей.

4)  Однако зачастую бывают ситуации, когда в качестве окружающей среды может выступать, например, конкурирующая фирма, военный противник, конкурент на выборах и т.п. В этом случае такая окружающая среда будет реагировать уже совсем не беспристрастно, а сугубо в своих интересах. Такая ситуация называется задачей принятия решения в условиях противодействия.

Раздел 2. Принятие решения в условиях риска 2.1 Постановка задачи

Рассмотрим следующую ситуацию.

Представьте что вы – глава пенсионного фонда Украины. На счета пенсионного фонда Украины поступают налоговые отчисления по достаточно большой процентной (большей, чем в большинстве развитых странах) ставке. По расчетам этих денег должно хватить на выплату пенсий сегодняшним пенсионерам и на накопление для выплат сегодняшним налогоплательщикам, по достижении ими пенсионного возраста. Ваша непосредственная обязанность, как главы пенсионного фонда обеспечить выполнение этих двух задач. Первая задача – выплата текущих пенсий – это чисто техническое задание. Будем считать, что с ним вы блестяще справитесь.

А что делать с накоплениями? Если эти деньги не трогать и "заморозить", то через несколько лет ввиду инфляции сегодняшний налогоплательщик получит сущие гроши. Естественным выходом (так делают во всем мире) будет эти средства во что-нибудь вложить (инвестировать).

Допустим, что вы, как инвестор, имеете возможность вложить средства пенсионного фонда Украины в один из четырех финансовых институтов: акции кампании г-на Сороса, в депозит Bank of America, в облигации госказначейства США и в золото. Эти четыре альтернативы (ваши возможные стратегии) обозначим А1, А2, А3, А4 .

Допустим, окружающая среда (В), в данном случае, ситуация на финансовом рынке на момент завершения депозита может принять одно из пяти определенных состояний. Эти пять состояний обозначим В1, В2, В3, В4, В5 .

Из многолетних статистических данных известны приближенные вероятности (Q) этих состояний: q1, q2, q3, q4, q5 .

Инвестиционная привлекательность проекта вложения средств определяется как конечная рентабельность. Оценка рентабельности считается известной для каждой стратегии инвестора и каждого состояния окружающей среды. Эти данные представлены в матрице, называемой матрицей выигрышей инвестора (игрока А),

где аij – это рентабельность инвестиционного проекта при выборе Аi-той альтернативы и при Вj-том состоянии окружающей среды.

От вас, как главы пенсионного фонда Украины, требуется выбрать наилучший вариант вложения средств налогоплательщиков.

Отметим, что понятие наилучшего исхода в различных условиях трактуется по-разному. Для различных условий принятия решений разработаны различные критерии выбора ЛПР наилучшего исхода. Решим данную задачу с помощью различных критериев.

2.2 Критерий Байеса

 

Критерий Байеса (принцип математического ожидания) предполагает полное доверие ЛПР известным вероятностям состояний окружающей среды. Следовательно, данная задача – это задача принятия решения в условиях риска.

Показатель эффективности стратегии Аi по критерию Байеса находится по формуле:

Z =  ,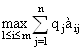

гдеm – количество строк матрицы, заданной в условии;

n – количество столбцов матрицы, заданной в условии;

qj – заданные вероятности ;

аij – элементы матрицы, заданной в условии.

Для случая оптимизации потерь критерий будет таким:

Z =  #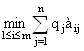

Заметим, что 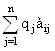 – это математическое ожидание стратегии Аi . Таким образом, исходную матрицу необходимо дополнить справа еще одним столбцом, в который нужно внести значения математических ожиданий всех стратегий:

Пример вычислений для первой строки:

 = 0,33 + 0,27 + 0,153 + 0,115 + 0,256 = 0,6 + 1,4 + 0,45 + 1,5 + 1,5 = 5,75

Далее в добавленном столбце нужно найти наибольший элемент (наибольшее математическое ожидание). Строка, в которой он стоит и будет оптимальной стратегией. Необходимо заметить, что наибольших элементов может быть несколько, тогда и оптимальных стратегий соответственно будет несколько.

В нашем случае наибольший элемент 5,95 (в матрице он выделен). Таким образом, в нашем примере оптимальной стратегией будет А3, т.е. средства фонда вам нужно вложить в третий проект.

Ответ А3 .

2.3 Критерий Лапласа (Бернулли)

 

Критерий Лапласа (принцип недостаточного основания) предполагает недоверие ЛПР известным вероятностям состояний окружающей среды. Вероятности состояний окружающей среды считаются одинаковыми и равными  . Следовательно, данная задача – это задача принятия решения в условиях риска с вероятностями  .

Показатель эффективности стратегии Аi по критерию Лапласа находится аналогично критерию Байеса с вероятностями  :

Z =  =  ,

Заметим, что нет необходимости вычислять эти математические ожидания. Достаточно просто просуммировать элементы строк матрицы и выбрать из них максимальную сумму:

Z =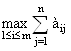

Для случая оптимизации потерь критерий будет таким:

Z =  #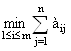

Таким образом, исходную матрицу необходимо дополнить справа еще одним столбцом, в который нужно внести значения сумм элементов строк всех стратегий:

Далее в добавленном столбце нужно найти наибольший элемент. Строка, в которой он стоит и будет оптимальной стратегией. Необходимо заметить, что наибольших элементов может быть несколько, тогда и оптимальных стратегий соответственно будет несколько.

В нашем случае наибольший элемент в добавленном столбце 34 (в матрице он выделен). Таким образом, в нашем примере оптимальной стратегией будет А1 , т.е. инвестор должен выбрать для вложения первый проект.

Ответ А1 .

2.4 Критерий Гермейера

Критерий Гермейера применяется для задач принятия решений в условиях риска.

Он применяется в основном для решения задач выбора для оптимизации величины потерь или затрат. Такие задачи довольно часто встречаются в хозяйственной практике. Матрица потерь, задаваемая в условии, будет содержать отрицательные элементы (потери выражаются отрицательными величинами). Если в матрице помимо отрицательных будут и положительные элементы, то исходная матрица потерь преобразуется в матрицу, содержащую только отрицательные элементы по правилу:

аij – с ,

где с – некое выбранное ЛПР положительное число.

Следует иметь в виду, что оптимальное решение зависит от выбора с.

Критерий Гермейера применяется и для оптимизации величины прибыли (как в нашей задаче), т.е. для положительных матриц.

В общем случае Гермейер предложил ввести в рассмотрение матрицу с такими элементами:

Построим новую матрицу для нашего примера:

Далее к этой матрице применяется принцип максимина. Показатель эффективности стратегии Аi при этом находится по формуле:

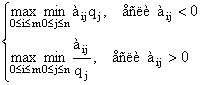
Таким образом, новую матрицу необходимо дополнить справа еще одним столбцом, в который нужно внести наименьшие значения элементов каждой строки.

Затем из элементов добавленного столбца нужно выбрать наибольший. Строка, в которой он стоит и будет оптимальной стратегией.

В нашем случае наибольший элемент в добавленном столбце 16 (в матрице он выделен). Таким образом, в нашем примере оптимальной стратегией будет А3, т.е. инвестор должен выбрать для вложения третий проект.

Ответ А3 .

2.5 Критерий Ходжа-Лемана

Критерий Ходжа-Лемана привносит фактор определенной субъективности при принятии решения.

Решение принимается в условиях риска. Однако у ЛПР есть некое недоверие к распределению вероятностей состояний окружающей среды. Поэтому ЛПР вводит некий "коэффициент доверия" l к вероятностям состояний окружающей среды (0 £ l £ 1). Чтобы сильно не рисковать, обычно таким коэффициентом берут 0,4. Этот коэффициент ещё называют уровнем оптимизма.

Показатель эффективности стратегии Аi по критерию Ходжа-Лемана находится по формуле:

Z =  ,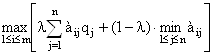

#Для случая оптимизации потерь критерий будет таким:

Z =  #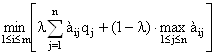

Таким образом, исходную матрицу необходимо дополнить справа еще тремя столбцами. В первый нужно внести значения математических ожиданий всех стратегий, умноженных на уровень оптимизма l = 0,4. Во второй нужно внести значения наименьших элементов всех строк, умноженных на уровень пессимизма 1 – l = 1 – 0,4 = 0,6 . В третий добавленный столбец внесем сумму значений первых двух добавленных столбцов:

Пример вычислений для первой строки:

 = 0,4  (0,33 + 0,27 + 0,153 + 0,115 + 0,256) = 0,4  5,75 = 2,3

 = 0,6  3 = 1,8

Z1 = 2,3 + 1,8 = 4,1

Далее в добавленном столбце нужно найти наибольший элемент. Строка, в которой он стоит и будет оптимальной стратегией.

В нашем случае наибольший элемент 4,78 (в матрице он выделен). Таким образом, в нашем примере оптимальной стратегией будет А3, т.е. инвестор для вложения должен выбрать третий проект.

Ответ А3 .

Раздел 3. Принятие решения в условиях неопределенности 3.1 Принцип максимина

Решим поставленную выше задачу при принятии решения в условиях неопределенности. В таких условиях также нет единой трактовки понятия наилучшего исхода. Поэтому данную задачу тоже будем решать с помощью различных критериев.

Принцип максимина (критерий Вальда) предполагает полное недоверие ЛПР известным вероятностям состояний окружающей среды. Либо же вероятности состояний окружающей среды считаются неизвестными. Следовательно, данная задача – это задача принятия решения в условиях неопределенности.

При неопределенности выбор наилучшей стратегии может основываться на введении различных разумных гипотез о поведении окружающей среды.

Одна из важнейших и основополагающих гипотез такого типа называется гипотезой антагонизма. Она состоит в предположении, что окружающая среда ведет себя наихудшим для ЛПР образом. На этой гипотезе основывается принцип максимина, называемый также принципом гарантированного результата.

Показатель эффективности стратегии Аi по критерию максимина находится по формуле:

Z =

Для случая оптимизации потерь критерий превратится в минимаксный и будет таким:

Z = #

Таким образом, исходную матрицу необходимо дополнить справа еще одним столбцом, в который нужно внести значения минимальных элементов каждой строки.

Затем из элементов добавленного столбца нужно выбрать наибольший. Строка, в которой он стоит и будет оптимальной стратегией.

Выбранные таким образом альтернативы полностью исключают всякий риск! Это означает, что ЛПР не может столкнуться с худшим результатом, чем тот на который он ориентируется. В силу этого принцип максимина является принципом крайнего пессимизма ЛПР (принципом наибольшей осторожности).

Как бы ни вела себя окружающая среда, результат не может оказаться ниже значения критерия максимина! Это свойство делает принцип максимина наиболее применяемым на практике, особенно в случаях, где от конечного результата зависят жизни людей.

Народная интуиция уже веками непроизвольно использует принцип максимина. Это подтверждается такими поговорками как "Семь раз отмерь – один раз отрежь", "Береженого бог бережет", "Лучше синица в руках, чем журавль в небе".

В нашем случае наибольший элемент в добавленном столбце 4 (в матрице он выделен). Таким образом, в нашем примере оптимальной стратегией будет А3, т.е. инвестор должен выбрать для вложения средств третий проект.

Ответ А3 .

3.2 Критерий азартного игрока

Критерий азартного игрока (принцип максимакса) – это диаметральная противоположность принципу максимина, он тоже применяется при принятии решения в условиях неопределенности. Критерий азартного игрока допустим в случаях очень низкого риска, а также когда выигрыш намного превышает возможные потери.

Показатель эффективности стратегии Аi по критерию азартного игрока находится по формуле:

Z =

Для случая оптимизации потерь критерий будет таким:

Z = #

Таким образом, исходную матрицу необходимо дополнить справа еще одним столбцом, в который нужно внести значения максимальных элементов каждой строки.

Затем из элементов добавленного столбца нужно выбрать наибольший. Строка, в которой он стоит и будет оптимальной стратегией.

В нашем случае наибольший элемент в добавленном столбце 15 (в матрице он выделен). Таким образом, в нашем примере оптимальной стратегией будет А1, т.е. инвестор должен выбрать для вложения первый проект.

Применение критерия азартного игрока народная мудрость выразила пословицей "Кто не рискует, тот не пьет шампанского".

Ответ А1 .

3.3 Критерий произведений

 

Критерий произведений тоже применяется при принятии решения в условиях неопределенности. Это более нейтральный критерий по сравнению с принципом максимина и критерием азартного игрока. Критерий произведений производит некое "выравнивание" между большими и малыми значениями аij .

Показатель эффективности стратегии Аi по критерию произведений находится по формуле:

Z =

Для случая оптимизации потерь критерий будет таким:

Z =  #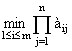

Таким образом, исходную матрицу необходимо дополнить справа еще одним столбцом, в который нужно внести значения произведений всех элементов каждой строки.

Затем из элементов добавленного столбца нужно выбрать наибольший. Строка, в которой он стоит и будет оптимальной стратегией.

В нашем случае наибольший элемент в добавленном столбце 8640 (в матрице он выделен). Таким образом, в нашем примере оптимальной стратегией будет А3, т.е. инвестор должен выбрать для вложения третий проект.

Ответ А3 .

3.5 Критерий Сэвиджа

Решение опять принимается в условиях неопределенности.

Сэвидж предложил ввести в рассмотрение новую матрицу, элементы которой определяются по формуле:

rij =

Построим новую матрицу для нашего примера:

Пример вычислений для первого столбца:

= 6; r11 = 6 – 3 = 3; r21 = 6 – 4 = 2; r31 = 6 – 6 = 0; r41 = 6 – 3 = 3.

Построенная таким способом матрица называется "матрицей сожалений". И действительно, ведь каждый элемент rij выражает "сожаление" ЛПР по поводу того, что он не выбрал наилучшего решения по отношению к

Далее к матрице сожалений применяется критерий минимакса. Показатель эффективности стратегии Аi при этом находится по формуле:

Z =  =

Для случая оптимизации потерь критерий будет таким:

Z =  #

Таким образом, матрицу сожалений необходимо дополнить справа еще одним столбцом, в который нужно внести наибольшие значения элементов каждой строки.

Затем из элементов добавленного столбца нужно выбрать наименьший. Строка, в которой он стоит и будет оптимальной стратегией.

В нашем случае наименьший элемент в добавленном столбце 5 (в матрице он выделен). Таким образом, в нашем примере оптимальной стратегией будет А3, т.е. инвестор должен выбрать для вложения третий проект.

Ответ А3 .

3.6 Критерий Гурвица

Решение принимается в условиях неопределенности.

Гурвиц предложил критерий, показатель эффективности стратегии Аi при котором находится где-то между точками зрения крайнего оптимизма (критерий азартного игрока) и крайнего пессимизма (критерий максимина). Для этого вводят некий коэффициент l – уровень пессимизма. Выбор уровня пессимизма – процесс субъективный. Чаще всего его выбирают равным либо 0,6 либо 0,5. После этого показатель эффективности стратегии Аi по критерию Гурвица находится по формуле:

Z =

Для случая оптимизации потерь критерий будет таким:

Z = #

Таким образом, исходную матрицу необходимо дополнить справа еще тремя столбцами. В первый нужно внести значения наименьших элементов всех строк, умноженных на уровень пессимизма l = 0,6. Во второй нужно внести значения наибольших элементов всех строк, умноженных на уровень оптимизма 1 – l = 1 – 0,6 = 0,4 . В третий добавленный столбец внесем сумму значений первых двух добавленных столбцов:

Затем из элементов добавленного столбца нужно выбрать наибольший. Строка, в которой он стоит и будет оптимальной стратегией.

В нашем случае наибольший элемент в добавленном столбце 7,2 (в матрице он выделен). Таким образом, в нашем примере оптимальной стратегией будет А1, т.е. инвестор должен выбрать для вложения средств первый проект.

Ответ А1 .

Раздел 4. Принятие решения в условиях противодействия 4.1 Матричные игры

 

Раздел "Теории принятия решений" в условиях противодействия называется теорией игр. А так как в основном условия задач в "Теории принятия решений" задаются в виде матриц, то рассматриваемые конфликтные ситуации называются матричными играми. В матричных играх состояниями В1, В2, …, Вn управляет не беспристрастная природа, а активный противник, преследующий сугубо свои цели.

ЛПР, управляющий своими стратегиями (ходами) А1, А2, …, Аn, и его противник, управляющий стратегиями (ходами) В1, В2, …, Вn в данной ситуации называются игроками.

Элементы матрицы аij , заданной в условии, называются выигрышами (платежами) игрока А. А вся матрица называется матрицей платежей.

Далее возможны два случая. Если в матричной игре задана одна платежная матрица, то естественно предположить, что выигрыши первого игрока будут являться проигрышами второго игрока. Такая антагонистическая ситуация называется матричной игрой с нулевой суммой. Цель игры для первого игрока (ЛПР) – побольше выиграть, а для второго игрока – поменьше проиграть. Иными словами, целью игры является определение оптимальной стратегии для каждого игрока – такой стратегии, при которой выигрыш первого игрока будет максимальным, а проигрыш второго игрока будет минимальным.

Однако, такая ситуация бывает не всегда. Зачастую в жизни ваш противник преследует сугубо свои цели, определенные своими выигрышами. В этом случае матричная игра задается двумя платежными матрицами. Или для краткости элементы одной платежной матрицы состоят из двух чисел: (аij, bij). Такая ситуация называется матричной игрой с ненулевой суммой. И для первого и для второго игроков цель игры – побольше выиграть.

Очевидно, что рассмотренная матричная игра предполагает, что каждый игрок делает только по одному ходу. Естественно, что многие конфликтные ситуации предполагают по нескольку ходов каждого игрока. Такие игры рассматриваются пошагово и решаются методами динамического программирования. На каждом отдельном шаге такая игра рассматривается как игра с одним ходом.

Матричные игры для двух игроков с нулевой и ненулевой суммой достаточно хорошо изучены и для них разработана теория оптимального поведения игроков.

Однако в жизненной практике в конфликтных ситуациях зачастую участвуют более чем две стороны. Чем больше игроков – тем больше проблем. Такие игры менее изучены и здесь есть просторное поле для новых фундаментальных научных исследований.

Несмотря на несколько легкомысленное звучание основных терминов, теория игр является строго научной дисциплиной с точными математическими выкладками.

На протяжении всего своего исторического пути развития человечество ежедневно сталкивается с конфликтными ситуациями: политическими, военными, экономическими, социальными и прочими, которые проявляются как в глобальных, так и в малых (вплоть до личных) формах. И если бы Человеку хватило бы ума в конфликтных ситуациях пользоваться не силой, не надеждой на "авось", а математикой, то жизнь наверняка была бы другой. Будем надеяться, что новое поколение, усвоив курс "Исследование операций" J, изменит жизнь к лучшему!

Итак, рассмотрим игру, в которой ЛПР противостоит "думающий" противник.

Возможны такие случаи:

1)  Ходы игроками делаются одновременно.

2)  Первым ходит игрок 2 – противник, но игрок 1 – ЛПР, не имеет информации о ходе противника.

3)  Первым ходит игрок 2 – противник, но игрок 1 – ЛПР, знает о ходе противника.

4)  Первым ходит игрок 1, но игрок 2 не имеет информации о ходе противника.

5)  Первым ходит игрок 1, но игрок 2 знает о ходе противника.

Очевидно, что случаи 1), 2) и 4) идентичны – никто из игроков не знает о ходе противника ничего.

Рассмотрим случай 3). Так как ЛПР имеет полную информацию о ходе противника, то мы имеем ситуацию принятия решения в условиях полной определенности. Как уже отмечалось выше, такими задачами занимается математическое программирование.

Рассмотрим случай 5). Так как ЛПР ходит первым, то его противник наверняка выберет самую худшую для ЛПР стратегию. Поэтому в такой ситуации ЛПР необходимо принимать решение о своем ходе согласно принципу наибольшей осторожности, т.е. согласно принципу максимина. Это утверждение однозначно, легко математически доказывается и не должно подвергаться сомнению ни в каких жизненных ситуациях.

Итак, содержательны по своей сути только случаи 1), 2) и 4), которые сводятся к одному случаю. Это как мы видим, принятие решения в условиях неопределенности.

4.2 Матричные игры, разрешимые в чистых стратегиях

Рассмотрим парную конечную антагонистическую игру. Пусть игрок А располагает m личными стратегиями, которые обозначим А1, а2 ..., Аm. Пусть у игрока В имеется n личных стратегий, обозначим их В1, В2, ,.., Вn. Говорят, что игра имеет размерность m х n . В результате выбора игроками любой пары стратегий Аi и Вj (i = 1,2 …, m; j = 1,2, …, n).

Однозначно определяется исход игры, т.е. выигрыш аij игрока А (положительный или отрицательный) и проигрыш (-аij) игрока В . Предположим, что значения аij известны для любой пары стратегий (Аi Вj). Значения этих выигрышей заданы в платежной матрице

Строки этой таблицы соответствуют стратегиям игрока А , а столбцы – стратегиям игрока В .

С помощью хорошо нам знакомого принципа максимина найдем гарантированный наибольший выигрыш для игрока А:

Найденное число a называется нижней ценой игры.

Стратегия, соответствующая максимину, называется максиминной стратегией – она будет оптимальной стратегией игрока А.

Посмотрим на эту ситуацию с точки зрения второго игрока: ему необходимо уменьшить свои потери. В таком случае критерию максимина превратится в минимаксный и гарантированный наименьший проигрыш для игрока В будет таким:

Найденное число в называется верхней ценой игры

Стратегия, соответствующая минимаксу, называется минимаксной стратегией – она будет оптимальной стратегией игрока В.

Причем, для нижней и верхней цены игры всегда справедливо неравенство:

Если нижняя и верхняя цены игры совпадают, то общее значение верхней и нижней цены игры a = в = n называется чистой ценой игры, или ценой игры. Элемент платежной матрицы, в котором достигается чистая цена игры, называется седловой точкой (по аналогии с поверхностью седла, которая искривляется вверх в одном направлении и вниз – в другом). Найденные оптимальные стратегии игроков А и В в данном случае называются чистыми стратегиями.

Матричная игра с платежной матрицей, имеющей седловую точку, называется игрой, разрешимой в чистых стратегиях. При этом очевидно, что решение игры обладает устойчивостью, т.е. если один из игроков придерживается своей оптимальной стратегии, то для другого не может быть выгодным отклоняться от своей оптимальной стратегии. Оба игрока находятся в "положении равновесия", из которого не выгодно выходить каждому.

Рассмотрим числовой пример.

Пусть имеем игру с платежной матрицей:

Проверим, имеет ли наша матричная игра седловую точку? Для этого используем принцип максимина.

Дополним исходную матрицу справа еще одним столбцом, а снизу – еще одной строкой. В них будем заносить значения минимальных элементов каждой строки и значения максимальных элементов каждого столбца соответственно:

Найдем нижнюю цену игры. Выигрыш игрока А:

a =  = 4он достигается в третьей строке.

Найдем верхнюю цену игры. Выигрыш игрока В:

в =  = 4 он достигается во втором столбце.

Как видим, выигрыши игроков совпадают: a = в = n = 4 , значит у матрицы имеется седловая точка. А значит, у данной матричной игры имеется пара оптимальных чистых стратегий А3В2 . Цена игры n = 4.

Но такое бывает далеко не всегда.

4.2 Матричные игры, разрешимые в смешанных стратегиях

 

4.2.1 Постановка задачи

Если платежная матрица не имеет седловой точки, то  . А значит  . Такая игра в чистых стратегиях не разрешима. Первый игрок в таком случае будет стремиться увеличить свой выигрыш, а второй – уменьшить свой проигрыш. Поиск такого решения приводит к применению сложной стратегии, состоящей в случайном применении двух и более чистых стратегий с определенными вероятностями:

PA = (p1, p2, …, pm) где pi – это вероятности применения чистых стратегий игроком А;

QB = (q1, q2, …, qn) где qj – это вероятности применения чистых стратегий игроком B;

при этом и  .

Такие наборы вероятностей применения чистых стратегий игроками А и В называются смешанными стратегиями.

Заметим, что чистые стратегии – это частный случай смешанных стратегий. Например, чистая стратегия первого игрока – это смешанная стратегия, у которой все вероятности pi = 0 , кроме соответствующего номера k чистой стратегии: pk = 1 .

Основная теорема теории игр (Теорема фон-Неймана): любая конечная игра двух лиц с нулевой суммой разрешима в смешанных стратегиях.

Как же искать смешанные стратегии? Их можно найти точно – алгебраическим способом (в частности, с помощью симплекс-метода) или графическим способом (для игры размерности 2 х n или m х 2 ).

Для того чтобы точно найти решение матричной игры в смешанных стратегиях, нужно представить заданную матричную игру в виде задачи линейного программирования и решить её симплекс-методом.

Рассмотрим матричную игру, не разрешимую в чистых стратегиях, в общем виде:

Заметим, что в матричной игре, разрешимой в чистых стратегиях, элементы платежной матрицы могут быть как положительными, так и отрицательными. Для симплекс-метода, которым будем решать игру, не разрешимую в чистых стратегиях, необходимо, чтобы элементы платежной матрицы были неотрицательными. Для этого, если в платежной матрице будут отрицательные элементы, нужно ко всем элементам платежной матрицы прибавить достаточно большое число с . При этом решение задачи не изменится, а цена игры увеличится на с.#

PA = (p1, p2, …, pm)– это оптимальная смешанная стратегия первого игрока. Её применение гарантирует первому игроку выигрыш не меньший, чем цена игры n . Если при этом второй игрок выберет стратегию В1, математически все вышесказанное будет иметь вид:

а11р1 + а21р2 + … + am1pm ≥ n

Таких неравенств будет столько, сколько есть возможных альтернатив у второго игрока, т.е. столбцов платежной матрицы – n штук:

а11р1 + а21р2 + … + am1pm ≥ n

а12р1 + а22р2 + … + am2pm ≥ n

а1nр1 + а2nр2 + … + amnpm ≥ n

Разделив все неравенства на n , получим (в общем виде):

а1j + а2j + … + amj ≥ 1

Обозначим:  = xi, . С помощью таких новых переменных вышеуказанные неравенства запишутся в виде:

а11 x1 + а21 x2 + … + am1 xm ≥ 1

а12 x1 + а22 x2 + … + am2 xm ≥ 1

а1n x1 + а2n x2 + … + amn xm ≥ 1

Просуммируем новые переменные:

 = x1 + x2 + … + xm =  +  + … +  =  =

PA = (p1, p2, …, pm)– это оптимальная смешанная стратегия первого игрока. То есть нужно так подобрать (p1, p2, …, pm) , чтобы n была как можно большей. Или же, что то же самое, чтобы  была как можно меньшей.

Таким образом, используя новые переменные и учитывая всё вышесказанное, исходную матричную игру можно представить в виде задачи линейного программирования:

найти вектор переменных Х = {x1, x2, … , xm}, такой что:

целевая функция f =  min

при множестве ограничений:

АТХ ≥ Е

гдеА – матрица коэффициентов (платежная матрица), заданная в условии;

Е – единичный вектор

Х – вектор неизвестных переменных, такой что xi =  ;

n – это цена игры:n =  =  ;

рi – это коэффициенты вектора смешанной стратегии первого игрока.

4.2.2 Решение задачи симплекс-методом

Рассмотрим числовой пример.

Пусть имеем игру с платежной матрицей:

Проверим, имеет ли наша матричная игра седловую точку? Для этого используем принцип максимина.

Выигрыш игрока А:a =  = 2 он достигается в первой строке.

Выигрыш игрока В:в =  = 3 он достигается в четвертом столбце.

Как видим, выигрыши игроков не совпадают, значит у матрицы нет седловой точки. Значит, нужно искать смешанные стратегии.

В данном конкретном случае в множестве ограничений будет четыре неравенства (т.к. в условии задачи четыре столбца). Пересчитывать симплекс- таблицы с четырьмя строками не очень сильно хочется, поэтому удобнее решить двойственную задачу (для коэффициентов вектора смешанной стратегии второго игрока), в которой будет всего две строки (т.к. в условии задачи две строки):

найти вектор двойственных переменных Y = {y1, y2, … yn}, такой что:

целевая функция g =  max

при множестве ограничений:АY ≤ Е

Для нашего примера задача линейного программирования будет такой:

найти вектор Y = {y1, y2, y3, y4}, такой что:

целевая функция g =  max

при множестве ограничений:

Далее нужно вспомнить методику применения симплекс-метода и использовать её для нашей задачи.

Однако, как показывает многолетняя практика, студенты обладают так называемой "краткосрочной памятью", которая работает только до сдачи необходимого экзамена. Поэтому вспомнить сейчас методику применения симплекс-метода вряд ли кто-то сможет. Для этого нужно сходить в библиотеку, найти специальную литературу и умело ей воспользоваться. Осмелимся заметить, что и этого половина студентов сделать поленится и благополучно завалит данную тему J . #

Поэтому для всеобщего блага приведем здесь методику применения симплекс-метода (пройденного и успешно сданного в математическом программировании) для нашей конкретной задачи.

1 этап – приведение задачи линейного программирования к каноническому виду.

Неравенства во множестве ограничений нужно превратить в равенства с помощью добавления искусственных переменных. Для того чтобы неравенства превратить в равенства, надо в каждое неравенство добавить (или отнять – в зависимости от знака неравенства) искусственную переменную:

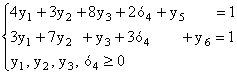
Целевая функция при этом будет выглядеть так:g = y1 + y2 + y3 + y4 + 0y5 + 0y6