Навигация
Вероятность невозможного события равна 0: P(Ø)=0
2. Вероятность невозможного события равна 0: P(Ø)=0.
3. Вероятность произведения независимых событий равна произведению вероятностей этих событий: Р(АВ)=Р(А)Р(В).
Пример: Преступник имеет 3 ключа. В темноте он открывает дверь, выбирая ключ случайным образом. На открытие каждой из дверей он тратит 5 секунд. Найти вероятность того, что он откроет все двери за 15 секунд.
Решение. Пусть событие А – “открыты все двери”. Разобьем это событие на более простые. Пусть В – “открыта 1-я“, С – “ открыта 2-я“, а D – “ открыта 3-я“. Тогда, А=ВСD по определению произведения событий. Следовательно Р(А)=Р(ВСD). По теореме о вероятности произведения независимых событий Р(ВСD) = Р(В)Р(C)Р(D).
Определение. Условной вероятностью события А, при условии, что произошло событие В, называется отношение вероятностей P(АВ) к Р(В) и обозначается РА(В): 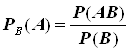 .
.
Пример: Бросается игральный кубик. Какова вероятность того, что выпало число очков, больше трех (событие А), если известно, что выпала четная грань (событие В)?
Решение. Событию В соответствует выпадение чисел 2,4,6. Событию А выпадение чисел 4, 5, 6. Событию А![]() В – 4, 6. Поэтому, используя формулу условной вероятности получим:
В – 4, 6. Поэтому, используя формулу условной вероятности получим: 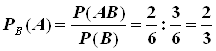 .
.
4. Вероятность произведения зависимых событий равна:
P(AВ)=Р(А)РА(В).
Пример: Изменим задачу: считаем, что преступник – забывчивый человек. Пусть преступник открыв дверь, оставляет ключ в ней. Какова тогда вероятность, что он откроет все двери за 15 сек?
Решение. Событие А – “открыты все двери”. Опять, А=ВСD по определению произведения событий. Следовательно Р(А)=Р(ВСD). Но, теперь события В, C и D – зависимы. По теореме о вероятности произведения зависимых событий Р(ВСD) = Р(В)Р(C|B) Р(D|BC).
Вычислим вероятности : Р(В)=1/3, РВ(С)=1/2 (ключа осталось только два и один из них подходит!), РBC(D)=1/1 и, значит, Р(А)=1/6 .
5. Вероятность суммы несовместных событий равна сумме их вероятностей.
Р(А1+ А2+…+ Аn)=Р(А1)+ Р(А2)+…+ Р(Аn).
Пример: В урне 5 белых, 20 красных и 10 черных шаров, не отличающихся по размеру. Шары тщательно перемешивают и затем наугад вынимают 1 шар. Какова вероятность того, что вынутый шар окажется белым или черным?
Решение. Пусть событие А – появление белого или черного шара. Разобьем это событие на более простые. Пусть В1 – появление белого шара, а В2 – черного. Тогда, А=В1+В2 по определению суммы событий. Следовательно Р(А)=Р(В1+В2). Так как В1 и В2 – несовместные события, то по теореме о вероятности суммы несовместных событий Р(В1+В2) = Р(В1)+Р(В2).
6.Вероятность суммы произвольных событий равна сумме их вероятностей без вероятности произведения событий
Р(А+В)=Р(А)+Р(В)-Р(АВ).
В общем случае данная формулы выглядит так:
![]() .
.
Пример: Ведутся поиски двух преступников. Каждый из них независимо от другого может быть обнаружен в течение суток с вероятностью 0,5. Какова вероятность того, что в течение суток будет обнаружен хотя бы один преступник?
Решение. Пусть событие А – “обнаружен хотя бы один преступник”. Разобьем это событие на более простые. Пусть В1 – обнаружен первый преступник, а В2 – обнаружен второй преступник. Тогда, А=В1+В2 по определению суммы событий. Следовательно Р(А)=Р(В1+В2). Так как В1и В2 – совместные события, то по теореме о вероятности суммы событий
Р(В1+В2) = Р(В1)+Р(В2)-Р(В1 В2) = 0,5+0,5 – 0,25=0,75.
Занятие 61. Задумано двузначное число. Найти вероятность того, что задуманным числом окажется: а) случайно названное двузначное число: б) случайно названное двузначное число, цифры которого различны?
2. Монета брошена два раза найти вероятность, что хотя бы один раз появится герб.
3. В коробке имеется шесть одинаковых жетонов с различными номерами. По одному наудачу извлекают все кубики. Найти вероятность того, что номера извлеченных кубиков появятся в возрастающем порядке.
4. В ящике имеется 15 деталей, среди которых 10 окрашенных. Сборщик наудачу извлекает три детали. Найдите вероятность того, что извлеченные детали окажутся окрашенными.
5. В волейбольной команде 6 мастеров спорта и 4 кандидата. Наудачу выбранным семи человекам дали премию. Найти вероятность того, что среди получивших премию окажутся три кандидата в мастера спорта?
6. В коробке пять одинаковых изделий, причем три из них окрашены. Наудачу извлечены два изделия. Найти вероятность того, что среди двух извлеченных изделий окажутся: а) одно окрашенное изделие; б) два окрашенных изделия; в) хотя бы одно окрашенное изделие.
7. В ящике 10 деталей, из которых четыре окрашены. Сборщик наудачу взял три детали. Найти вероятность того, что хотя бы одна из взятых деталей окрашена.
8. Два стрелка стреляют в мишень. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,7, а для второго 0,8. Найти вероятность того, что при одном залпе в мишень попадет только один из стрелков.
Домашнее задание
1. Монету бросают два раза. Найти вероятность того, что хотя бы один раз появится герб.
2. Какова вероятность того, что из шести отмеченных чисел в карточке «Спортлото» (игра из 49) k чисел будут выигрышными.
3. Вероятность одного попадания в цель при одном залпе из двух орудий равна 0,38. Найти вероятность поражения цели при одном выстреле первым из орудий, если известно, что для второго орудия эта вероятность равна 0,8.
Занятие 71. Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что изделие стандартно, равна 0,9. Найти вероятность, того, что из двух проверенных изделий только одно стандартное.
2. Брошены три игральные кости. Найти вероятность следующих событий: а) на двух выпавших гранях появиться одно очко, а на третьей грани – другое число очков.
3. Вероятность попадания в мишень стрелком при одном выстреле равна 0,8. Сколько выстрелов должен произвести стрелок, чтобы с вероятностью, меньшей 0,4 можно было ожидать, что не будет ни одного промаха?
4. В читальном зале имеется шесть учебников по теории вероятности, из которых три в переплете. Библиотекарь наудачу взял два учебника. Найти вероятность того, что оба учебника окажутся в переплете.
5. Среди 100 лотерейных билетов есть 5 выигрышных. Найти вероятность того, что 2 наудачу выбранные билета окажутся выигрышными.
6. В цехе работают 7 мужчин и три женщины. Наудачу отобраны три человека. Найти вероятность того, что все отобранные лица окажутся мужчинами.
7. Студент знает 20 из 25 вопросов программы. Найти вероятность того, что студент знает предложенные ему экзаменаторам три вопроса.
Домашнее задание
1. В ящике 10 деталей, среди которых шесть окрашенных. Сборщик наудачу извлекает четыре детали. Найти вероятность того, что все извлеченные детали окажутся окрашенными.
2. Вероятности того, что нужная деталь находится в первом, втором, третьем, четвертом ящике соответственно равны 0,6; 0,7; 0,8; 0,9. Найти вероятности того, что деталь содержится: а) не более чем в трех ящиках; б) не менее чем в двух ящиках.
Занятие 8Определение. Совокупность событий А1, А2, …, Аnназывается полной группой событий, если выполняются следующие условия:
а) она описывает все возможные исходы;
б) события попарно независимы и не совместны.
Пусть дано событие А, оно может наступить при появлении одного из несовместных Событий В1, В2,…, Вn, которые образуют полную группу. Нам также известны вероятности ![]() ,
, ![]() , …,
, …, ![]() . Как можно найти вероятность события А? Ответ на этот вопрос дает.
. Как можно найти вероятность события А? Ответ на этот вопрос дает.
Вероятность события А, которое может наступить лишь при условии появлении одного из несовместных событий В1, В2,…, Вn, образующих полную группу, равна сумме произведений вероятности каждого из этих событий на собственную условную вероятность:
![]() .
.
Эту формулу также называют формулой полной вероятности.
Пример: В проведении операции по освобождению заложников участвуют 2 группы снайперов: 10 человек с винтовкой ОП21 и 20 человек с АКМ47. Вероятность поражения из ОП21 – 0,85, а АКМ47 – 0,65. Найти вероятность того, что при одном выстреле произвольного снайпера преступник будет поражен.
Решение. Пусть событие А – “преступник поражен”. Разобьем это событие на более простые. Преступник может быть поражен либо из ОП21, либо из АКМ47. Вероятность того, что произвольный снайпер вооружен ОП21 (событие Н1) равна 10/30. Вероятность того, что произвольный снайпер вооружен АКМ47 (событие Н2) равна 20/30.
Вероятность того, что преступник поражен равна:
![]()
Составим задачу: Пусть дано событие А, оно может наступить при появлении одного из несовместных Событий В1, В2,…, Вn, которые образуют полную группу. Так как нам заранее не известно, какое событие наступит, их называют гипотезами. Допустим, что произведено испытание в результате, которого появилось событие А. Поставим своей задачей определить как изменились вероятности гипотез, в связи с тем что событие А уже наступило. Другими словами определим следующие условные вероятности:
![]() ,
, ![]() , …,
, …, ![]() .
.
Определить данные вероятности можно при помощи формулы Бейеса:
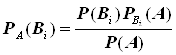 ,
,
Заменив ![]() получим:
получим:
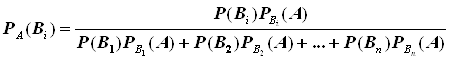 .
.
Пример: На склад поступило 1000 подшипников. Из них 200 изготовлены на 1-м заводе, 460–на 2-м и 340 – на 3-м. Вероятность того, что подшипник окажется нестандартным, для 1-го завода равна 0,03, для 2-го – 0,02, для 3-го – 0,01. Взятый наудачу подшипник оказался нестандартным. Какова вероятность того, что он изготовлен 1-м заводом?
Решение: Пусть A – событие, состоящее в том, что взятый Подшипник нестандартный, а – Н1, Н2, Н3, гипотезы, что он изготовлен соответственно 1-м, 2-м или 3-м заводом. Вероятности указанных гипотез составляют : P(H1)=200/1000=0.2, P(H2)=460/1000=0.46, P(H1)=340/1000=0.34.
Из условия задачи следует, что р1=РН1(А)=0,03; р2=РН2(А)=0,02; р3=РН3(А)=0,01.
Найдем вероятность того, что подшипник, оказавшийся нестандартным, изготовлен 1-м заводом. По формуле Бейеса имеем:
![]()
1. Среди N экзаменационных билетов n «счастливых». Студенты подходят за билетами один за другим. У кого больше вероятность взять счастливый билет: у того, кто подошел первым, или у того, кто подошел вторым? Какова вероятность взять «счастливый» билет у последнего студента?
2. Экзаменационных билетов содержат по 2 вопроса, которые не повторяются. Экзаменующийся может ответить только на 25 вопросов. Определить вероятность того, что экзамен будет сдан, если для этого достаточно ответить на два вопроса из одного билета или на один вопрос из первого билета и на указанный дополнительный вопрос из другого билета.
3. Во время испытаний было установлено, что вероятность безотказной работы прибора при отсутствии повреждений равна 0,99, при перегреве – 0,95, при вибрации – 0,9, при вибрации и перегреве – 0,8. Найти вероятность P1 отказа этого прибора во время работы в жарких странах (вероятность перегрева – 0,2, вибрации – 0,1) и вероятность P2 отказа во время работы в передвигающейся лаборатории (вероятность перегрева – 0,1, вибрации – 0,3), если считать перегрев и вибрацию независимыми событиями.
4. По каналу связи передают символы A, B, C с вероятностями 0,4; 0,3; 0,3 соответственно. Вероятность искажения символа равна 0,4, и все искажения равновероятны. Для увеличения надежности каждый символ повторяют четыре раза. На выходе восприняли последовательность ВАСВ. Какова вероятность того, что передали АААА, ВВВВ, СССС?
5. На наблюдательной станции установлены 4 радиолокатора различных конструкций. Вероятность обнаружения целей с помощью первого локатора равна 0,86, второго 0,9, третьего 0,92, четвертого 0,95. Наблюдатель наугад включает один из локаторов. Какова вероятность обнаружения цели?
6. Вероятность того, что двое близнецов будут одного пола 0,64, а вероятность рождения в двойне первым мальчика 0,51. Найти вероятность того, что второй из близнецов будет мальчиком, при условии, что первый из них мальчик.
Домашнее задание
1. Некоторая деталь производиться на двух заводах. Известно, что объем продукции первого завода в к раз превышает объем второго. Доля брака на первом заводе 0,3, на втором 0,2. Наугад взятая деталь оказалась бракованной. Какова вероятность того, что эта деталь выпущена первым заводом?
2. Среди женщин – избирателей 70% поддерживают кандидата А, а среди мужчин 60%. Используя данные переписи, согласно которым доля женщин избирателей составляет 55%, оценить вероятность победы на выборах кандидата А.
3. Трое сотрудников фирмы выдают соответственно 30%, 50%, 20% всех изделий, производимой фирмой. У первого брак 2%, второго 5%, третьего 1%. Какова вероятность, что случайно выбранное изделие дефектно?
Занятие 10Изучение случайных величин требует связи этих величин с определенными событиями, которые заключаются в попадании случайной величины в некоторый интервал и для которых определены вероятности. Другими словами необходимо связать случайную величину с полем данного испытания.
Для лучшего понимания рассмотрим пример. При бросании кости могли появиться цифры 1, 2, 3, 4, 5, 6. Наперед определить число выпавших очков невозможно, так как это зависит от многих случайных величин, которые полностью не могут быть учтены. В этом смысле число очков есть величина случайная; и числа 1, 2, 3, 4, 5, 6 – есть возможные значения этой величины.
Определение: Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.
Будем обозначать случайные величины прописными (заглавными) буквами: X, Y, Z, а их возможные значения соответствующими строчными буквами x, y, z. Если величина Х имеет три значения то они будут обозначены так: х1, х2, х3 .
Обычно рассматриваются два типа случайных величин: дискретные и непрерывные.
Рассмотрим следующий пример: Число мальчиков пошедших в секцию бальных танцев среди 100 пришедших туда людей есть случайная величина, которая может принимать следующие значения 0, 1, 2, …, 100. Эти значения отделены друг от друга промежутками, в которых нет возможных значений Х . таким образом в этом примере случайная величина принимает отдельные изолированные значения.
Приведем второй пример: расстояние, которое пролетит диск при метании, есть величина случайная. Действительно величина зависит от многих факторов, например от ветра, температуры и других факторов, которые не могут быть полностью учтены. Возможные значения этой величины принадлежат некоторому промежутку (а;b).
В данном примере случайная величина может принять любое из значений промежутка (а;b). Здесь нельзя отделить одно возможное значение от другого промежутком, не содержащим возможных значений случайной величины.
Уже из сказанного можно заключить о том, что целесообразно будет различать случайные величины, принимающие лишь отдельные изолированные значения, и случайные величины, возможные значения которых сплошь заполняют некоторый промежуток.
Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным.
Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Очевидно, число возможных значений непрерывной случайной величины бесконечно.
Еще примерами непрерывных случайных величин могут быть спортивный результат в беге или прыжках, рост и масса тела человека, сила мышц и другие.
Закон распределения вероятностей дискретной случайной величины.
Для задания дискретной случайной величины не достаточно перечислить все возможные ее значения, нужно еще указать их вероятности.
Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями; его можно задать таблично, в виде формулы и графически.
При табличном задании первая строка содержит возможные значения, а вторая – их вероятности:
| Х | x1 | x2 | … | xn |
| p | p1 | p2 | … | pn |
Сумма вероятностей второй строки таблицы равнеа единице:
![]() .
.
Если множество возможных значений Х бесконечно, то ряд ![]() сходится и его сумма равна единице.
сходится и его сумма равна единице.
Для наглядности закон распределения дискретной случайной величины можно изобразить и графически, для чего в прямоугольной системе координат строят точки (хi; pi), а затем соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения.
Для непрерывной случайной величины график выглядит в виде кривой непрерывной на данном промежутке.
Занятие 11Как известно закон распределения полностью характеризует случайную величину. Однако часто закон распределения неизвестен и приходится ограничиваться меньшими сведениями. Также для решения многих задач не нужно знать распределения случайной величины, а достаточно знать лишь некоторые обобщающие числовые характеристики этого распределения.
Одной из таких характеристик является математическое ожидание. Для более наглядного определения рассмотрим подход к этому понятию на конкретном примере.
Пусть имеется дискретная случайная величина Х, которая может принимать значения х1, х2, …, хn. Вероятности которых соответственно равны р1, р2, …, рn. Тогда математическое ожидание М(Х) случайной величины Х определяется равенством:
![]() .
.
Пример: Найти математическое ожидание дискретной случайной величины Х, заданной законом распределения:
| Х | -4 | 6 | 10 |
| Р | 0,2 | 0,3 | 0,5 |
Решение: М(Х)=-4∙0,2+6∙0,3+10∙0,5=6
Математическое ожидание приближенно равно (тем точнее, чем больше число испытаний) среднему арифметическому наблюдаемых значений случайной величины.
На практике часто требуется оценить рассеяние возможных значений случайно величины вокруг ее среднего значения. Например, в артиллерии важно знать, насколько кучно лягут снаряды вблизи цели, которая должна быть поражена. Именно такие задачи решает дисперсия.
Определение: Дисперсией случайной величины Х называется математическое ожидание квадрата отклонений случайной величины от ее математического ожидания. Дисперсия обозначается, как D(x)
D(Х)=M[X-М(Х)]2=M[(x-x)2]
Пример: Найти дисперсию случайной величины Х, которая задана следующим законом распределения:
| Х | 1 | 2 | 5 |
| p | 0,3 | 0,5 | 0,2 |
Решение. Найдем математическое ожидание:
![]() .
.
По определению:
![]() .
.
Используя формулу D(Х)=M(X)2-[М(Х)]2 можно найти дисперсию гораздо быстрее:
![]() .
.
Для оценки рассеяния всевозможных значений случайной величины вокруг ее среднего значения кроме дисперсии служат и другие величины.
Средним квадратическим отклонением величины Х называют квадратный корень из дисперсии ![]()
1. Найти дисперсию дискретной случайной величины Х и построить многоугольник распределения, заданной законом распределения:
| Х | -4 | 6 | 10 |
| р | 0,2 | 0,3 | 0,5 |
а) б)
| Х | 0,21 | 0,54 | 0,61 |
| р | 0,1 | 0,5 | 0,4 |
В денежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в 50 р. и десять выигрышей по 1 р. Найти закон распределения случайной величины Х – стоимости возможного выигрыша для владельца лотерейного билета.
2. Дискретная случайная величина имеет только 2 возможных значения х и у, причем x<y. Вероятность того, что Х примет значение х =0,6. Найти закон распределения величины Х, если математическое ожидание и дисперсия известны: М(Х)=1,4, D(X)=0.24.
Занятие 13В практике статистических наблюдений различают два вида наблюдений:
· Сплошное (изучаются все объекты);
· Выборочное (несплошное, когда изучается часть объектов).
Примером сплошного наблюдения является перепись населения, охватывающее все население страны. Выборочными наблюдениями является, например, проводимые социологические исследования, охватывающие часть населения страны, области, района и т.д.
Определение: Вся подлежащая изучению совокупность объектов называется генеральной совокупностью.
Определение: Часть объектов, которая отобрана для непосредственного изучения из генеральной совокупности, называется выборочной совокупностью или выборкой.
Числа объектов в генеральной или выборочной совокупности называют их объемами. Генеральная совокупность может иметь конечный и бесконечный объем.
Сущность выборочного метода состоит в том, чтобы по некоторой части генеральной совокупности (по выборке) выносить суждение о ее свойствах в целом.
Преимущества выборочного метода:
· Экономия затраты ресурсов
· Единственно возможный в случае бесконечной генеральной совокупности или в случае, когда исследовании связано с уничтожением наблюдаемых объектов (например исследование долговечности электрических лампочек и т.д)
· Возможность углубленного исследования за счет расширения программы исследования при тех же затратах.
· Снижение ошибок регистрации.
Неизбежные ошибки, возникающие в связи с изучением части объектов, могут быть заранее оценены и по средствам правильной организации выборки сведены к незначимым величинам.
Между тем использование сплошного наблюдения часто приводит к снижению точности наблюдения, а это у же вызывает неустранимые ошибки, и может привести к снижению точности сплошного наблюдения по сравнению с выборочным.
Чтобы по данным выборки иметь возможность судить о генеральной совокупности, она должна быть отобрана случайно. На практике отбор может выполняться с помощью жеребьевки (лотереи) или с помощью случайных чисел.
Основной недостаток выборочного метода – ошибки исследования, называемые ошибками репрезентативности.
Выборка называемая репрезентативной (представительной), если она достаточно хорошо воспроизводит генеральную совокупность.
Виды выборок:
· собственно – случайная выборка (случайный выбор элементов без расчленения на части или группы)
· механическая выборка (элементы отбираются через определенный интервал)
· типическая выборка (выбор случайным образом элементов из типических групп, на которые по некоторому признаку разбивается генеральная совокупность)
· серийная выборка (случайным образом отбираются целые группы совокупности, а сами серии подвергаются сплошному наблюдению)
Способы образования выборки:
· повторный выбор – каждый элемент, случайно отобранный и обследованный, возвращается в общую совокупность и может быть повторно отобран.
· Бесповторный отбор – когда обратный элемент не возвращается в общую совокупность.
| Наименование характеристики | Генеральная совокупность | Выборка |
| Математическое ожидание |
|
|
| Дисперсия |
|
|
| Доля |
|
|
Где хi – значение признака.
N и n – объемы генеральной и выборочной совокупностей.
Ni и ni – число элементов генеральной и выборочной совокупностей со значением признака хi
M и m – число элементов генеральной и выборочной совокупностей, обладающих данным признаком
Пример: генеральная совокупность задана таблицей распределения:
| Xi | 2 | 4 | 5 | 6 |
| Ni | 8 | 9 | 10 | 3 |
Найти дисперсию.
![]()
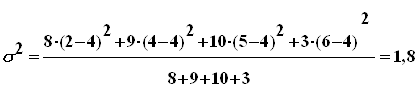
Важнейшей задачей выборочного метода является оценка параметров генеральной совокупности по данным выборки.
Занятие 14Рассмотрим пример:
Необходимо изучить изменение результатов спортсменов, занимающихся легкой атлетикой, по сравнению с предыдущим годом. Получены следующие данные результатов в процентах к предыдущему году: 97,8; 97,10; 101,17;,,,;142,3;141,02.(всего 100 значений.).
Различные значения признака (случайной величины Х) называется вариантами (обозначаем их через х).
Первый шаг к осмыслению – упорядочивание. Расположение вариантов в порядке возрастания (убывания), т.е. ранжирование вариантов ряда.
Следующим шагом произведем группировку, то есть разобьем на отдельные интервалы. Число интервалов не следует брать большим.
Числа показывающие, сколько раз встречаются варианты из данного интервала, называются частотами (ni), а отношение их к общему числу наблюдений частостями wi=n/ni. Частоты и частости называют весами.
| I | Результаты в процентах к предыдущему году х | Частота (количество спортсменов)ni | Частость (доля рабочих)wi=n/ni | Накопленная частота niнак | Накопленная частость wiнак= niнак/n |
| 1 | 94,0-100 | 3 | 0,03 | 3 | 0,03 |
| 2 | 100,0-106,0 | 7 | 0,07 | 10 | 0,10 |
| 3 | 106,0-112,0 | 11 | 0,11 | 21 | 0,21 |
| … | … | … | … | … | … |
| 8 | 136,0-142,0 | 2 | 0,02 | 100 | 1,00 |
| 100 | 1,00 |
Определение: Вариационным рядом называется ранжированный в порядке возрастания или убывания ряд вариантов с соответствующими им весами (частотами или частостями).
Определение: накопленная частота niнак показывает сколько наблюдалось вариантов со значениями признака меньших х.
Накопленная частость – отношение накопленной частоты к общему числу наблюдений: wiнак= niнак/n
Теперь полученный нами вариационный ряд позволяет выявить закономерности.
Для задания вариационного ряда достаточно указать варианты и соответствующие им частоты или частости.
Занятия 15-16Вариационный ряд называется дискретным, если любые его варианты отличаются на постоянную величину.
Вариационный ряд называется непрерывным, если варианты могут отличаться один от другого на сколь угодно малую величину.
В примере мы привели пример непрерывного ряда.
Для графического изображения вариационного ряда используются:
Полигон – служит для изображения дискретного вариационного ряда и представляет собой ломаную, в которой концы отрезков имеют (хi, ni).
Гистограмма служит для изображения интервальных вариационных рядов и представляет собой ступенчатую фигуру из прямоугольников с основаниями, равными интервалам значений признака к=х2-х1. И высоты равные частотам. Если соединить середины верхних оснований прямоугольников отрезками прямой, то можно получить полигон того же распределения.
Кумулятивная прямая (кумулята) – кривая накопленных частот. Для дискретных рядов кумулята представляет ломаную, соединяющую точки (хi, niнак ) или (хi, wiнак). Для интервального вариационного ряда ломаная начинается с точки, абсцисса, которой равна началу первого интервала, а ордината – накопленной частоте, равной нулю. Другие точки соответствуют концам интервалов.
Сформулируем принцип практической уверенности:
Если вероятность события А в данном испытании очень мала, то при однократном выполнении испытания можно быть уверенным в том, что событие А не произойдет, и в практической деятельности вести себя так, как будто событие А вообще невозможно.
Например: отправляясь самолетом в другой город, мы не рассчитываем на возможность погибнуть в авиа катастрофе, хотя вероятность такого события имеется.
Но при многократном повторении испытаний мы не можем считать маловероятное событие А практически невозможным.
Определение: Статистической гипотезой называется любое предположение о виде или параметрах неизвестного закона распределения.
Проверяемую гипотезу обычно называют нулевой и обозначают Н0. Также рассматривают альтернативную (конкурирующую гипотезу) Н1 являющуюся отрицанием Н0.
Суть проверки статистической гипотезы состоит в вычислении статистики данной выборки. Затем по выборочному распределению определятся критическое значение. Если статистика больше критического значения, то событие можно считать практически не возможным.
Сравнение двух совокупностей имеет важное практическое значение. На практике часто встречается случай, когда средний результат одной серии эксперимента отличается от среднего результата другой серии.
Пример: В промышленности данная задача возникает при выборочном контроле качества изделий, изготовленных на разных установках или при различных технологических режимах.
Пусть имеются две совокупности, характеризуемые генеральными средними х и у. И дисперсиями для которых найдены средние арифметические и выборочные дисперсии. Необходимо проверить гипотезу Н0 о равенстве генеральных средних. Тогда статистика находится по следующей формуле:
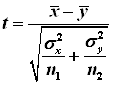
Если t>tкр то гипотеза Н0 отвергается. Если нет, то делается вывод что нулевая гипотеза не противоречит имеющимся наблюдениям.
Занятия 17 – 18Определение: Корреляционной зависимостью между двумя переменными величинами называется функциональная зависимость между значениями одной из них и условным математическим ожиданием другой.
Корреляционная зависимость может быть представлена в виде:
![]()
Это уравнение называют уравнением регрессии, а их графики линиями регрессии.
Для отыскания уравнений регрессий необходимо знать закон распределения двумерной случайной величины.
Данные о статистической зависимости удобно задавать в виде корреляционной таблицы.
| Вес (кг) (Х) | Середины интервалов | Рост (см) (у) | |||||
| 155-160 | 160-165 | 165-170 | 170-175 | Всего (ni) | Групповая Средняя | ||
| Хi yj | 157,5 | 162,5 | 167,5 | 172,5 | |||
| 40-45 | 42,5 | 2 | 1 | 7 | 10 | 168,5 | |
| 45-50 | 47,5 | 3 | 6 | 4 | 6 | 19 | 165,9 |
| 50-55 | 52,5 | 3 | 11 | 1 | 15 | 166,8 | |
| 60-65 | 62,5 | 2 | 1 | 2 | 5 | 162,5 | |
| 70-75 | 72,5 | 1 | 1 | 172,5 | |||
| Всего nj | 7 | 11 | 17 | 15 | 50 | ||
| Групповая средняя
| 50,4 | 49,8 | 52,5 | 47,2 | |||
Вычисленные групповые средние изобразим графически в виде ломанной, называемой эмпирической линией регрессии.
По виду ломанной можно предположить наличие линейной функциональной зависимости между случайными величинами Х и У, то есть имеется функция y=kx+b, где
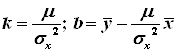
Где ![]() выборочная ковариация и равна:
выборочная ковариация и равна:
![]()
![]()
![]()
![]()
![]() К=-46,09 В=2471,02 У=-46,09х+2471,02
К=-46,09 В=2471,02 У=-46,09х+2471,02
1. В ходе исследования результатов забега на 100 метров юношами одиннадцатых классов двух групп – экспериментальной и контрольной – были получены данные, представленные в таблице.
2.
| Время (секунды) | 12,3-13,9 | 13,9-15,5 | 15,5-17,1 | 17,1-17,7 |
| Число юношей экспериментальной группы | 3 | 20 | 20 | 2 |
| Число юношей контрольной группы | 1 | 8 | 18 | 3 |
1) Изобразить данные графически, построив гистограммы для каждой группы.
2) Для каждой группы определить среднее значение, дисперсию, моду и медиану.
3) Проверить гипотезу о равенстве средних двух групп учащихся, используя критерий Стьюдента и полагая критическое значение статистики 1,67.
Домашняя работа.
В ходе исследования результатов высоты прыжка с места спортсменов – велосипедистов двух групп – экспериментальной и контрольной – были получены данные, представленные в таблице.
| Высота прыжка (см) | 37-45 | 45-53 | 53-61 | 61-69 |
| Число юношей экспериментальной группы | 4 | 20 | 10 | 1 |
| Число юношей контрольной группы | 2 | 15 | 20 | 3 |
1) Изобразить данные графически, построив гистограммы для каждой группы.
2) Для каждой группы определить среднее значение, дисперсию, моду и медиану.
3) Проверить гипотезу о равенстве средних двух групп учащихся, используя критерий Стьюдента и полагая критическое значение статистики 1,67.
Занятия 21-22
Подготовка к контрольной работе.
Комбинаторика:
1. Сколько четырехзначных чисел можно составить из цифр 1, 2, 3, 4, если каждая цифра входит в изображение числа только один раз.
2. Сколько можно составить сигналов из 6 флажков различного цвета, взятых по 2?
3. Сколькими способами можно выбрать 2 детали из ящика, содержащего 10 деталей?
4. Сколько существует двузначных чисел, у которых цифра десятков меньше цифры единиц?
5. В нашем распоряжении есть три различных флага. На флагштоке поднимается сигнал состоящий не менее, чем из двух флагов. Сколько различных сигналов можно поднять на флагштоке, если порядок флагов в сигнале учитывается.
6. В карточке игры «Русское лото» нужно зачеркнуть 6 чисел от 1 до 99. Сколькими способами это можно сделать?
7. Сколько различных имен – отчеств можно составить из имен Надежда, Иван, Андрей, Наталья, Дмитрий, Людмила, Александр?
8. Шесть ящиков занумерованы числами от 1 до 6. Сколькими способами можно разложить по этим ящикам 20 одинаковых шаров так, чтобы ни один ящик не оказался пустым?
Вероятность:
1. В партии 10 из деталей 7 стандартных. Найти вероятность того, что среди шести взятых наудачу деталей 4 стандартных.
2. В конверте среди 100 фотокарточек находится одна разыскиваемая. Из конверта наудачу извлечены 10 карточек. Найти вероятность того, что среди них окажется нужная.
3. В группе 12 студентов, среди которых 8 отличников. По списку наудачу отобраны 9 студентов. Найти вероятность того, что среди отобранных студентов пять отличников.
4. В урне 30 шаров: 10 красных, 5 синих, 15 белых. Найти вероятность появления цветного шара.
5. Стрелок стреляет по мишени, разделенной на 3 области. Вероятность попадания в первую область равна 0,45, во вторую 0,35. Найти вероятность, того, что стрелок при одном выстреле попадет либо в первую область, либо во вторую.
6. Брошены две игральные кости. Найти вероятность того, что: а) на каждой из выпавших граней появиться пять очков. Б) на всех выпавших гранях появиться одинаковое количество очков.
7. Найти вероятность совместного поражения цели двумя орудиями, если вероятность поражения цели первым орудием 0,8, а вторым 0,7.
8. Имеется 3 ящика, содержащие по 10 деталей. В первом ящике 8, во втором 7 и в третьем 9 стандартных деталей. Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что все три вынутые детали окажутся стандартными.
9. В урне 5 белых, 4 черных, 3 синих шара. Каждое испытание состоит в том, что наудачу извлекают один шар, не возвращая его обратно. Найти вероятность того, что при первом испытании появиться белый шар, при втором – черный и при третьем – синий.
10. В мешочке имеется 10 одинаковых кубиков с номерами от 1 до 10. Наудачу извлекают по одному три кубика. Найти вероятность того, что последовательно появятся кубики с номерами 1, 2, 3, если кубики извлекаются: а) без возвращения; б) с возвращением.
11. Вероятности попадания в цель при стрельбе из трех орудий: 0,8, 0,7, 0,9. Найти вероятность хотя бы одного попадания при одном залпе из всех орудий.
12. вероятности попадания в цель при стрельбе первого и второго орудий равны 0,7 и 0,8. Найти вероятность попадания при одном залпе хотя бы одним орудием.
13. Имеется два набора деталей. Вероятность того, что деталь первого набора стандартна, равна 0,8, а второго 0,9. Найти вероятность того, что взятая на удачу деталь (из наудачу взятого набора) – стандартная.
14. В первой коробке содержится 20 радиоламп, из них 18 стандартных, во второй коробке 10 ламп, из них 9 стандартных. Из второй коробки наудачу взята лампа и переложена в первую. Найти вероятность того, что лампа, наудачу извлеченная из первой коробки, будет стандартной.
15. Детали, изготовленные цехом завода, попадают для проверки их на стандартность к одному из двух контроллеров Вероятность того, деталь попадет к первому контроллеру равна 0,6, а ко второму 0,4. Вероятность того, что годная деталь будет признана стандартной первым контроллером 0,94, а вторым 0,98. Годная деталь при проверки была признана стандартной. Найти вероятность того, что эту деталь проверил первый контроллер.
16. Батарея из трех орудий произвела залп, причем два снаряда попали в цель. Найти вероятность того, что первое орудие дало попадание, если вероятности попадания цель первым, вторым и третьим орудиями равны: 0,4, 0,3 и 0,5.
Приложение 2
Самостоятельная работа № 1
1. Сколько существует двузначных чисел, у которых цифра десятков меньше цифры единиц?
2. В нашем распоряжении есть три различных флага. На флагштоке поднимается сигнал состоящий не менее, чем из двух флагов. Сколько различных сигналов можно поднять на флагштоке, если порядок флагов в сигнале учитывается.
3. В карточке игры «Русское лото» нужно зачеркнуть 6 чисел от 1 до 99. Сколькими способами это можно сделать?
4. Сколько различных имен – отчеств можно составить из имен Надежда, Иван, Андрей, Наталья, Дмитрий, Людмила, Александр?
5. Шесть ящиков занумерованы числами от 1 до 6. Сколькими способами можно разложить по этим ящикам 20 одинаковых шаров так, чтобы ни один ящик не оказался пустым?
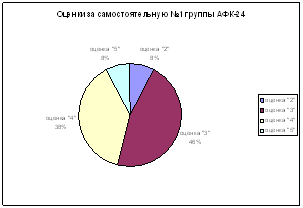
Самостоятельная работа № 2
1. Найти вероятность того, что при бросании трех игральных костей шестерка выпадает на одной (безразлично какой) кости, если на гранях двух других костей выпадут числа очков, не совпадающие между собой (и не равные шести).
2. Набирая номер телефона, абонент забыл последние три цифры и, помня лишь, что эти цифры различны, набрал их на удачу. Найти вероятность того, что набраны нужные цифры.
3. Из партии изделий товаровед отбирает изделия высшего сорта. Вероятность того, что наудачу взятое изделие окажется высшего сорта, равна 0,8. Найти вероятность того, что из трех проверенных изделий только два изделия высшего сорта.
4. Вероятности попадания в цель при стрельбе первого и второго орудий соответственно равны: 0,7 и 0,8. Найти вероятность попадания при одном залпе (из обоих орудий) хотя бы одним из орудий.
5. У сборщика имеется 3 конусных и 7 эллиптических валиков. Сборщик взял один валик, а затем второй. Найти вероятность того, что первый из взятых валиков – конусный, а второй эллиптический.
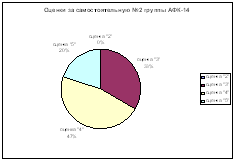
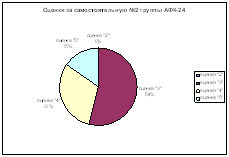
Самостоятельная работа № 3
1. В сборочный цех завода поступает 40% деталей из первого цеха и 60 процентов из второго. В цехе номер 1 производиться 90% стандартных деталей, а во втором 95%. Найти вероятность, того, что наудачу взятая деталь окажется стандартной? Найти вероятность того, что стандартная деталь изготовлена вторым цехом.
2. Из 40 экзаменационных билетов студент выучил только 30. Каким выгоднее ему зайти на экзамен, первым или вторым?
3. Прибор содержит две микросхемы. Вероятность выхода из строя в течение 10 лет первой микросхемы равна 0.007, а второй 0.1. Известно, что из строя вышла одна микросхема. Какова вероятность того, что вышла из строя первая микросхема?
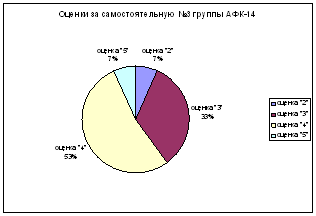
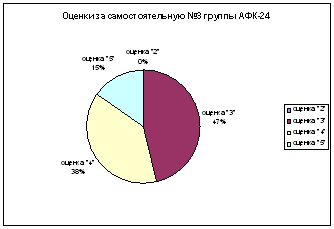
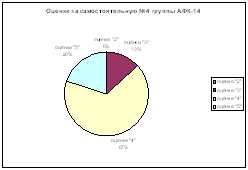
Самостоятельная работа № 4
1. Монета бросается 4 раза. Построить многоугольник распределения случайной величины Х – числа выпадений герба.
2. В урне 8 шаров, из которых 5 белых, остальные – черные. Из нее наудачу вынимают 3 шара. Найти закон распределения числа белых шаров. Вычислить Математическое ожидание и дисперсию.
3. Вероятность сдачи экзамена первым студентом 0.6, а вторым 0.9. Составить ряд распределения и вычислить ее математическое ожидание и дисперсию случайной величины Х – числа студентов, успешно сдавших экзамен в случае, когда: а) экзамены пересдавать нельзя; б) экзамен можно один раз пересдать.
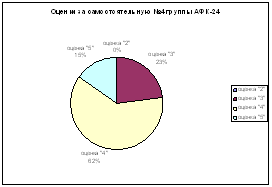
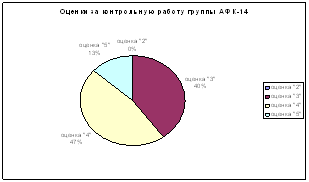
Контрольная работа
1. На каждой из семи одинаковых карточек напечатана одна из следующих букв о, п, т, к, н, и, с. Найдите вероятность того, что на четырех, вынутых по одной и расположенных в одну линию, карточках можно будет прочитать слово «кино».
2. В фирме работают 9 мужчин и 4 женщины. По табельным номерам наудачу отобрали 7 человек. Найти вероятность того, что среди отобранных лиц окажутся 2 женщины.
3. Два стрелка стреляют по мишеням. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0.7, для второго 0.85. Найти вероятность того, что при одном залпе в мишень попадает только один из стрелков.
4. В магазин завезли 3 коробки импортной обуви и 5 коробок отечественной. Вероятность того, что импортная обувь без брака – 0.8; отечественная – 0.7. Найти вероятность того, что наудачу извлеченная пара обуви из наудачу взятой коробки без брака.
5. В ходе исследования результатов забега на 100 метров юношами одиннадцатых классов двух групп – экспериментальной и контрольной – были получены данные, представленные в таблице.
| Время (секунды) | 12,3-13,9 | 13,9-15,5 | 15,5-17,1 | 17,1-17,7 |
| Число юношей экспериментальной группы | 3 | 20 | 20 | 2 |
| Число юношей контрольной группы | 1 | 8 | 18 | 3 |
Изобразить данные графически, построив гистограммы для каждой группы. Для каждой группы определить среднее значение, дисперсию, моду и медиану. Проверить гипотезу о равенстве средних двух групп учащихся, используя критерий Стьюдента и полагая критическое значение статистики 1,67.
Похожие работы
... ; технологическая функция имеет подфункции экономии учебного времени и учебного материала, устранения его дублирования и т.д. ГЛАВА 4. СОДЕРЖАНИЕ ИСНТРУМЕНТАЛЬНО-МЕТОДОЛОГИЧЕСКОГО ОБЕСПЕЧЕНИЯ ПЕДАГОГИЧЕСКОЙ ИНТЕГРАЦИИ 4.1. Типология интегративно-педагогического исследования В связи с поднимаемой в данном параграфе проблемой большой интерес вызывает монография В.М.Полонского "Оценки ...
... общего, начального и среднего профессионального образования, обеспечивающей наиболее полную реализацию интересов и образовательных потребностей учащихся. Таким образом, можно выделить несколько вариантов организации профильного обучения. 1) Модель внутришкольной профилизации В этой модели общеобразовательное учреждение может быть однопрофильным и многопрофильным. 2) Модель сетевой ...
... упражнения нормализуют деятельность желудочно-кишечного тракта: желудочное и кишечное сокоотделение, активность пищеварительных ферментов, моторную активность и т.д. Регулярные занятия физической культурой, сопровождаемые потоотделением, не только совершенствуют терморегуляцию, но и обеспечивают систематический вывод из организма образовавшихся в процессе жизнедеятельности шлаковых веществ. ...
... . В современном мире, чтобы быть профессионально компетентным, педагога должен постоянно учиться, заниматься самообразованием и самореализовываться в педагогической деятельности. Поэтому при формировании профессиональной компетентности будущего педагога, необходимо вести деятельность по двум направлениям: подготовке студентов как будущих педагогов и работа с преподавателями. Учитывая сложность и ...

0 комментариев