Модель Стоуна
Москва
2007
Содержание
Введение. 3
Решение задачи Стоуна для случая двух товаров. 4
Минимизация расходов потребителя: обратная задача. 7
Решение задачи Стоуна для случая трех товаров. 9
Пример 1. 9
Пример 2. 10
Пример 3. 11
Пример 4. 12
Пример 5. 14
Литература. 15
Введение
Пусть U – функция полезности потребителя. Задачу потребительского выбора можно записать в виде
![]() (*)
(*)
![]() ,
,
![]()
(Доход мы нормировали на единицу, не теряя общности). Набор товаров ![]() можно рассматривать в качестве минимальной корзины потребления. Для приобретения минимального набора
можно рассматривать в качестве минимальной корзины потребления. Для приобретения минимального набора ![]() необходимо, чтобы доход был больше стоимости этого набора, т.е.
необходимо, чтобы доход был больше стоимости этого набора, т.е.
![]() (**)
(**)
Показатели степеней ai > 0 характеризуют относительную "ценность" соответствующих товаров для потребителя. Добавив к функции (*) бюджетные ограничения (**), получим задачу потребительского выбора, которую называют моделью Р. Стоуна.
Решение задачи Стоуна для случая двух товаров
Выведем оптимум потребителя при покупке им двух благ X и Y (при необходимости число благ можно расширить до сколь угодно большого количества). Тогда наша задача состоит в том, чтобы максимизировать функцию полезности потребителя от этих двух благ – U (X, Y). Однако наш потребитель ограничен своим доходом (бюджетом), который он тратит без остатка на приобретение этих благ. В результате бюджет потребителя можно представить как I = PXX + PYY.
Затем мы решаем задачу на условный локальный максимум (максимум с ограничением) методом множителей Лагранжа. Составляем следующее уравнение
L = U (X, Y) + l(I - PXX - PYY), (1)
где l - так называемый «множитель Лагранжа». Его экономический смысл станет нам ясен несколько позже. Первое условие максимума с ограничениями получается в результате нахождения частных производных первого порядка по X, Y и l из уравнения (1) и приравнивания их к нулю.[1] Получаем систему уравнений (2)
![]()
![]() (2)
(2)
![]()
Последнее уравнение из (2) говорит нам о том, что доход (бюджет) потребителя расходуется на блага X и Y без остатка. Однако нас больше интересуют первые два уравнения из (3.А.2). Из них следует, что
![]() (3)
(3)
![]()
Правые части в (3) есть ни что иное, как MUX и MUY, то есть предельные полезности благ X и Y . Отсюда получаем сформулированное в основном тексте главы 2 условие оптимума потребителя.
![]() , (4)
, (4)
где l может быть интерпретирована как предельная полезность денежной единицы. Ведь для любого блага n MUn/Pn может трактоваться как темп возрастания полезности по мере увеличения затрат денег на покупку этого блага.
Для того, чтобы найти точки оптимума (или, что тоже самое, спрос на блага X и Y), надо знать функцию полезности. Допустим, U = XY. Тогда по методу Лагранжа получаем
![]()
![]() (5)
(5)
![]()
Решая систему уравнений (5) относительно X и Y получаем
![]() ,
, ![]()
Пусть, например, доход потребителя равен 100 д.е, PX = 2 д.е, PY = 5 д.е. Тогда X* = 25, Y* = 10. Если предположить, что PX стало равно 5 д.е., а PY снизилось до 4 д.е., то новые значения спроса на эти блага X* = 10, а Y* = 12,5.
Заметим, что в нашем случае функции спроса достаточно простые. Спрос зависят только от цены благ и дохода потребителя. В то же время они позволяют заметить, что
а) каждому значению цены блага и дохода отвечает одно значение спроса;
б) если все цены и доходы меняются в одной и той же пропорции, то спрос на блага не меняется.
Минимизация расходов потребителя: обратная задача
В предыдущем разделе математического приложения ставилась задача максимизировать полезность потребителя при ограниченном доходе. Теперь ставится обратная задача: как минимизировать расходы потребителя при постоянном значении функции полезности.
Эта проблема не является какой-то искусственно созданной математической задачей. Ей можно дать экономическое толкование. Представим данную кривую безразличия и соответствующее ей значение функции полезности как задающие определенный уровень жизни или уровень реального дохода потребителя. Тогда есть смысл спросить: каковы минимальные расходы, позволяющие достичь данный уровня жизни при некоторых фиксированных ценах? Такой подход также позволяет анализировать эффект ценовых изменений на эти расходы.
Теперь мы минимизируем I = PXX + PYY при ограничении U (X, Y) = ![]() , где
, где ![]() - определенный фиксированный уровень полезности. Составляем уравнение Лагранжа для этого случая
- определенный фиксированный уровень полезности. Составляем уравнение Лагранжа для этого случая
L = ( PXX
+ PYY) - m [U (X, Y) - ![]() ]
]
Тогда имеем
![]() (1)
(1)
![]()
![]()
![]()
Возьмем первые два уравнения из (1). Из них получаем
![]() , (2)
, (2)
где m - величина обратная предельной полезности денежной единицы, то есть равна 1/l. Если заменить в (2) m на 1/l и возвести уравнение в степень - 1, то получим знакомое нам условие оптимума потребителя, совпадающее с (4).
Решение задачи Стоуна для случая трех товаров Пример 1
Пусть функция полезности имеет вид
![]()
Бюджетное ограничение
![]()
составим фунцию Лагранжа
![]()
Найдем частные производные

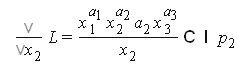
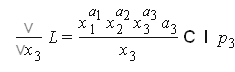
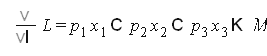
решение системы
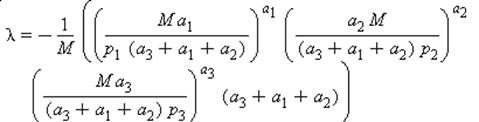
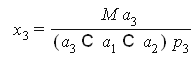
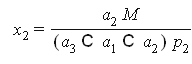
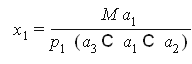
Пусть функция полезности имеет вид
![]()
Бюджетное ограничение
![]()
составим функцию Лагранжа
![]()
Найдем частные производные
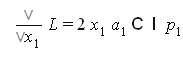
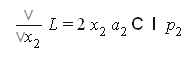
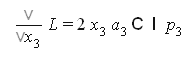
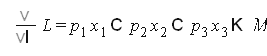
решение системы
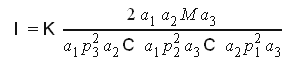
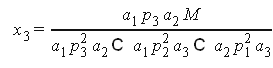
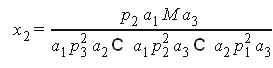
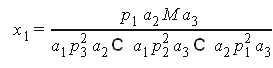
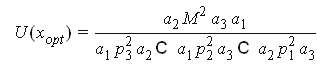
Пусть функция полезности имеет вид
![]()
Бюджетное ограничение
![]()
составим функцию Лагранжа
![]()
Найдем частные производные
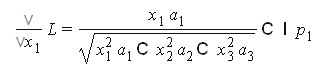
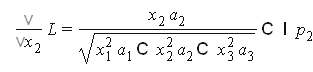
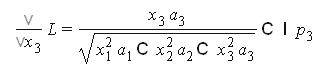
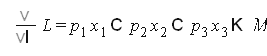
решение системы
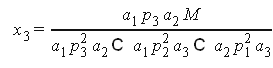
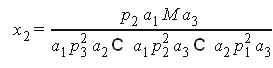
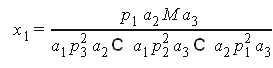
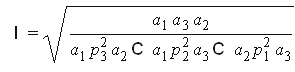
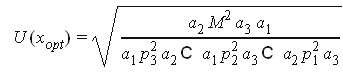
Пусть функция полезности имеет вид
![]()
Бюджетное ограничение
![]()
составим функцию Лагранжа
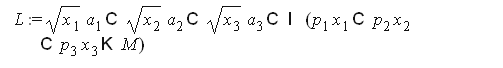
Найдем частные производные
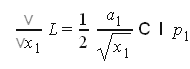
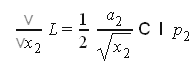
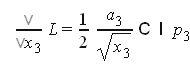
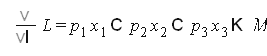
решение системы
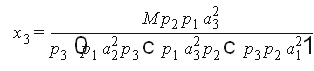
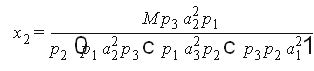
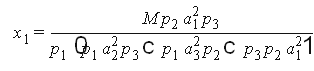
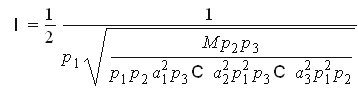
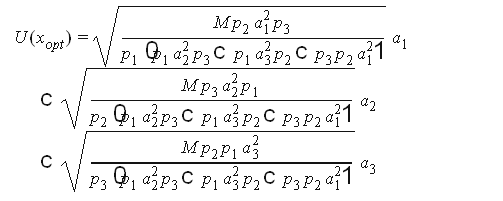
Пример 5
Пусть функция полезности имеет вид
![]()
Бюджетное ограничение
![]()
составим фунцию Лагранжа
![]()
Найдем частные производные
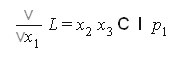
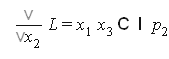
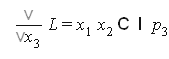
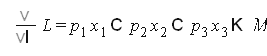
решение системы
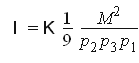
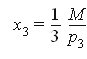
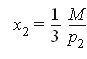
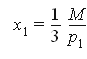
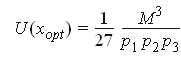
Литература
1. Экономика. Учебник / Под ред. А. С. Булатова. – М.: Юристъ, 2001.
2. Микроэкономика. Учебники МГУ им. М. В. Ломоносова / Под ред. А. В. Сидоровича. – М.: ДИС, 2002.
3. Экономическая теория (политэкономия). Учебник / Под ред. В. И. Видянина, Г. П. Журавлевой. – М.: РЭА, 2000.
4. Курс экономики. Учебник / Под ред.Б. А. Райзберга. – М.: ИНФРА-М, 2000.
5. Экономическая теория. Учебник / Под ред. В. Д. Камаева. – М.: Владос, 2001.
6. Экономическая теория. Учебник / Под ред. В. И. Видянина, А. И. Добрынина, Г. П. Журавлевой, Л. С. Тарасевича. – М.: ИНФРА-М, 2000.
7. Микроэкономика. Учебник / Под ред. Е. Строганова, И. Андреева. – М.: Питер, 2002.
[1] Условия второго порядка базируются на сложных математической технике и ничего дополнительно изучающему начальный курс экономики не дают.
Похожие работы
... . В конце XIX наблюдался огромный рост аренды и залога ферм. Таким образом, при вступлении США в монополистическую стадию развития почти 3/5 фермеров оказались, по данным официальной статистики, в зависимости от финансового капитала. 5. Нобелевский лауреат 1984 года по экономике Ричард Стоун Известный английский экономист Ричард Стоун родился в 1913 г. в Лондоне. Окончив в 1935 г. ...
... столичную группу образуют г. Астана, Акмолинская область. 3-ую группу образуют многонаселенные области – ЮКО, Карагандинская, Алматинская области. 9. Первый вариант оценок субъективных предпочтений интернет-услуг частным бизнесом Рассмотрим систему показателей, которая позволяет провести косвенную оценку реакции потребителя интернет-услуг, выражающую в увеличении объема потребляемых услуг, а ...
... Чистая прибыль 209217 Рентабельность реализации, % 23.25 Посленалоговая рентабельность увеличилась с 22,67 до значения 23,25 %. Поэтому изменение кредитной политики целесообразно. 3. ДЕЛОВАЯ СИТУАЦИЯ ПО УПРАВЛЕНИЮ ДЕНЕЖНЫМИ СРЕДСТВАМИ И ЛИКВИДНЫМИ ЦЕННЫМИ БУМАГАМИ Финансовый менеджер компании по производству одежды для лыжного спорта занимается прогнозированием потребности в денежных ...
... благ (продуктов) Учитывая структуру цен, доход и собственные предпочтения, потребитель приобретает определённое количество благ, и математическая модель такого его поведения называется моделью потребительского выбора. В некоторых задачах выделяют один продукт, а вторым считают все остальные. Поэтому сначала рассмотрим модель с двумя видами продуктов. Потребительский набор – это вектор (x1,x2), ...


0 комментариев