Навигация
Математическое ожидание
1. Математическое ожидание
![]()
М(Х) совпадает, в силу симметрии распределения, с медианой.
Моды равномерное распределение не имеет.
Дисперсия
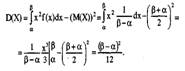
Отсюда, среднее квадратическое отклонение
![]()
Третий центральный момент
![]()
поэтому распределение симметрично относительно М(Х).
Четвёртый центральный момент

Вероятность попадания СВ в заданный интервал (а;b). Пусть СВ X распределена по равномерному закону,
18. Закон больших чисел
Под законом больших чисел в теории вероятностей понимают совокупность теорем, в которых утверждается, что существует связь между средним арифметическим достаточно большого числа случайных величин и средним арифметическим их математических ожиданий.
В1927 г. Гейзенберг открыл принцип неопределенности, который утверждает, что измерительное познание ограничено. Неопределенность является неотъемлемой частью нашей жизни, однако, при большом числе однотипных опытов можно установить определенные закономерности.
19. Нормальный закон распределения
Нормальный закон распределения играет исключительную роль в теории вероятностей. Это наиболее часто встречающийся закон распределения, главной особенностью которого является то, что он является предельным законом, к которому, при определённых условиях, приближаются другие законы распределения.
Дифференциальная функция нормального закона имеет вид
![]()
Числовые характеристики нормального закона:
1. Математическое ожидание характеризует центр распределения
![]()
где ex=exp(x);
2. Дисперсия характеризует форму распределения
![]()
Свойства дифференциальной функции нормального закона:
1. Область определения: Df = R;
2. Ось ОХ - горизонтальная асимптота;
3. х = а±σ - две точки перегиба;
4. Максимум в точке с координатами (а; 1/(σ√2π);
5. График симметричен относительно прямой х=а;
6. Моменты:
μ1=μ3=…=μ2k+1=…=0,
μ2=σ2, μ4=3σ4,
Sk=μ3/σ3=0, Ex=μ4/σ4-3=0
7. Вероятность попадания нормально распределенной случайной величины в заданный интервал определяется, по свойству интегральной функции
![]()
где
![]()
интегральная функция нормального закона (рис.14); Ф(х)- функция Лапласа.
Свойства интегральной функции нормального закона:
1. Ф* (-∞)=0;
2. Ф*(+)=1;
3. Ф*(x)=1/2+Ф(x);
4. Ф*(-x)=1-Ф*(x).
Вероятность заданного отклонения. Правило трех сигм.
Найдем вероятность того, что случайная величина X, распределённая по нормальному закону, отклонится от математического ожидания М(Х)=а не более чем на величину ε>0.
Р(|х-а|<ε)= Р(-ε< х-а<+ε) = Р(а-ε<х< а+е) =Ф*((a+ε-a)/σ)-Ф*((a-ε-a)/σ)=Ф*(ε/σ)-(1-Ф* (ε/σ))=2Ф* (ε/σ)-1.
Или, используя функцию Лапласа:
P(|X-a|<ε)=2Ф(ε/σ).
Найдём вероятность того, что нормально распределённая СВ X отклонится от M(X)=a на σ, 2σ, 3σ:
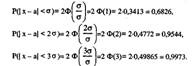
Отсюда следует правило Зσ. если случайная величина X имеет нормальное распределение, то отклонение этой случайной величины от ее математического ожидания по абсолютной величине не превышает утроенное среднее квадратическое отклонение (Зσ).
20. Многомерные случайные величины
В практических задачах приходится сталкиваться со случаями, когда результат описывается двумя и более случайными величинами, образующими систему случайных величин (случайный вектор). Например, точка попадания снаряда имеет две координаты: х и у, которые можно принять за систему случайных величин, определенных на одном и том же пространстве элементарных событий Ω.
Закон распределения дискретной двумерной случайной величины можно представить в виде таблицы, характеризующей собой совокупность всех значений случайных величин и соответствующих вероятностей:
| x1 | x2 | … | xn | Σ P(yj) | |
| y1 | P(x1,y1) | P(x2,y2) | … | P(xn,y1) | P(y1) |
| y2 | P(x1,y2) | P(x2,y2) | … | P(xn,y2) | P(y2) |
| … | … | … | … | … | … |
| ym | P(x1,ym) | P(x2,ym) | … | P(xn,ym) | P(ym) |
| Σ Pxi | P(x1) | P(x2) | … | P(xn) | 1 |
В общем случае двумерная случайная величина задается в виде интегральной функции, которая означает вероятность попадания двумерной случайной величины в квадрант левее и ниже точки с координатами (х, y):
F(x, у) = Р(Х<х, Y<y).
21. Свойства интегральной функции:
1. F - не убывает и непрерывна слева по каждому аргументу.
2. F(-∞, у)= F(x,-∞)= F(-∞, -∞)= 0.
3. F(+∞, у)= F2(y) - функция распределения случайной величины Y. F(x,+∞)= F1,(x) - функция распределения случайной величины X.
4. F(+∞,+∞)=l.
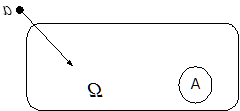
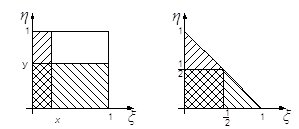
Вероятность попадания двумерной случайной величины в прямоугольник определяется исходя из определения интегральной функции двумерной случайной величины:
Р((х, у) c D) = F(β,δ) - F(α,β) - F(β,γ) + F(α,γ).

Рис. Вероятность попадания точки (х, у) в прямоугольник D
Случайные величины X, Y независимы, если
F(x, у) = = F1(x)* F2(y).
Дифференциальная функция системы двух непрерывных случайных величин определяется как вторая смешанная производная функции распределения:
f(x,y)=(∂2F(x,y))/∂x∂y=F″xy(x,y).
Свойства дифференциальной функции:
l.f(x,y)>0;
![]()
![]()
Геометрически свойство 2 означает, что объем тела, ограниченного поверхностью f (x, у) и плоскостью XOY, равен 1.
Если случайные величины X и Y независимы, то
f(x,y) = f1(x) f2(y), где f1(x)=F’1(x),f2(y)=F’2(y).
В противном случае f ( x , у ) = f1( x ) f ( y / x ) или f ( x, y) = f2( y ) f (x / y ), где f(y/x)=f(x,y)/f1(x) - условная дифференциальная функция CB Y при заданном значении X = x, f(y/x)=f(x,y)/f2(x) - условная дифференциальная функция СВ X при заданном значении Y= у;![]() - дифференциальные функции отдельных случайных величин X и Y, входящих в систему.
- дифференциальные функции отдельных случайных величин X и Y, входящих в систему.
Похожие работы
... Доказать: По определению второй смешанной производной. Найдем по двумерной плотности одномерные плотности случайных величин X и Y. Т.к. полученное равенство верно для всех х, то подинтегральные выражение аналогично В математической теории вероятности вводится как базовая формула (1) ибо предлагается, что плотность вероятности как аналитическая функция может не существовать. Но т.к. в нашем ...
... равна 0,515). Конец 19 в. и 1-я половина 20 в. отмечены открытием большого числа статистических закономерностей в физике, химии, биологии и т.п. Возможность применения методов теории вероятностей к изучению статистических закономерностей, относящихся к весьма далёким друг от друга областям науки, основана на том, что вероятности событий всегда удовлетворяют некоторым простым соотношениям, о ...
... {ξn (ω )}¥n=1 . Поэтому, во-первых, можно говорить о знакомой из математического анализа (почти) поточечной сходимости последовательностей функций: о сходимости «почти всюду», которую в теории вероятностей называют сходимостью «почти наверное». Определение 46. Говорят, что последовательность с. в. {ξn } сходится почти наверное к с. в. ξ при n ® ¥ , и пишут: ξn ...
... ничего другого, кроме как опять же события и . Действительно, имеем: *=, *=, =, =. Другим примером алгебры событий L является совокупность из четырех событий: . В самом деле: *=,*=,=,. 2.Вероятность. Теория вероятностей изучает случайные события. Это значит, что до определенного момента времени, вообще говоря, нельзя сказать заранее о случайном событии А произойдет это событие или нет. Только ...
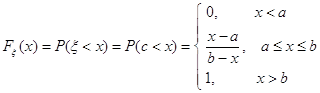
0 комментариев