Навигация
Локальная формула Муавра-Лапласа
7. Локальная формула Муавра-Лапласа
Если npq>10 , то
![]()
где вероятность р отлична от 0 и 1 (р→0,5), х =(k-np)/√npq.
Для облегчения вычислений функция
![]()
представлена в виде таблицы (прил.1).
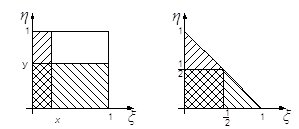
φ(х) - функция вероятности нормального распределения (рис. 6) имеет следующие свойства:
1) φ(х)-четная;
2) точки перегиба х = ± 1;
3) при х≥5, φ(х)→0, поэтому функция φ(х) представлена в виде таблицы для 0≤х≤5 (прил.1).
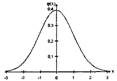
Рис. Функция вероятности нормального распределения
8. Интегральная теорема Муавра-Лапласа.
При больших значениях n , для вычисления вероятности того, что произойдет от к1, до к2 событий по схеме
![]()
Бернулли, используется интегральная формула Муавра-Лапласа
Pn(k1≤k≤k2)=Ф(x2)- Ф(x1),
где x1=(k1-np) /(√npq), x2=(k2-np)/(√npq), Ф(x) – функция Лапласа. (рис.7)
Ф(х) имеет следующие свойства:
1. Ф(-х)= -Ф(х) - функция нечетная, поэтому достаточно изучать её для неотрицательных значений х

2. Функция Ф(х) возрастает на всей числовой оси;

Рис. Функция Лапласа
3. При х≥5, Ф(х)→1/2 (y = 0,5 горизонтальная асимптота при х>0), поэтому функция представлена в виде таблицы Для 0≤х≤5 (прил.1).
4. Вероятность отклонения относительной частоты от постоянной вероятности в независимых испытаниях не более чем на некоторое число ε>0
![]()
9. Формула Пуассона
Если npq<10 и р<0,1, то
![]() где λ=np.
где λ=np.
10. Случайные величины и их виды
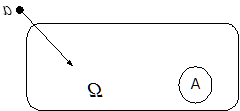
Случайной величиной (СВ) называют такую величину, которая в результате опыта может принимать те или иные значения, причем до опыта мы не можем сказать какое именно значение она примет. (Более точно, СВ - это действительная функция, определенная на пространстве элементарных событий Q). Случайные величины обозначаются последними буквами латинского алфавита - X,Y,Z. Случайные величины могут быть трех типов: - дискретные, - непрерывные, - смешанные (дискретно-непрерывные). Дискретная случайная величина (ДСВ) может принимать конечное или бесконечное счетное число значений. Непрерывная случайная величина (НСВ) в отличие от ДСВ принимает бесконечное несчетное число значений. Например мишень имеет форму круга радиуса R. По этой мишени произвели выстрел с обязательным попаданием. Обозначим через Y расстояние от центра мишени до точки попадания, Ye [0; R]. Y - непрерывная случайная величина, так как она принимает бесконечное несчетное число значений.
Пусть X - дискретная случайная величина, которая принимает значения х1, х2, ...,хn,... с некоторой вероятностью рi, где i = 1, 2, ..., n,... Тогда можно говорить о вероятности того, что случайная величина X приняла значение хi: рi=Р(Х=хi).
ДСВ может также представляться в виде многоугольника распределения – фигуры, состоящей из точек, соединенных отрезками. Над СВ устанавливаются операции сложения и умножения.
Суммой двух СВ X и Y наз-ся случайная величина, которая получается в рез-те сложения всех значений случайной величины X и всех значений СВ Y, соответствующие вероятности перемножаются. Произведением двух СВ X и Y наз-ся СВ, которая получается в рез-те перемножения всех значений СВ X и всех значений СВ Y, соответствующие вероятности перемножаются.
11. Математическое ожидание
Математическим ожиданием М(Х) ДСВ X называется среднее значение случайной величины:
![]()
Или иначе, М(Х) - это сумма парных произведений случайной величины на соответствующую вероятность:
![]()
Мода Мо(Х) распределения - это значение СВ, имеющее наиболее вероятное значение.
Медиана Ме(Х) - это значение случайной величины, которое делит таблицу распределения на две части таким образом, что вероятность попадания в одну из них равна 0,5. Медиана обычно не определяется для ДСВ.
Свойства математического ожидания:
1) М(С)=С, где С=const;
2)М(СХ) = СМ(Х);
3) M(X±Y) = М(Х) ± M(Y);
4) Если случайные величины X и Y, независимы, то M(XY) = M(X)*M(Y).
Для биномиального распределения М(Х)=nр;
для геометрического распределения М(Х)= 1/р;
для распределения Пуассона М(Х)=λ;
для гипергеометрического распределения М(Х) = n(M/N).
Похожие работы
... Доказать: По определению второй смешанной производной. Найдем по двумерной плотности одномерные плотности случайных величин X и Y. Т.к. полученное равенство верно для всех х, то подинтегральные выражение аналогично В математической теории вероятности вводится как базовая формула (1) ибо предлагается, что плотность вероятности как аналитическая функция может не существовать. Но т.к. в нашем ...
... равна 0,515). Конец 19 в. и 1-я половина 20 в. отмечены открытием большого числа статистических закономерностей в физике, химии, биологии и т.п. Возможность применения методов теории вероятностей к изучению статистических закономерностей, относящихся к весьма далёким друг от друга областям науки, основана на том, что вероятности событий всегда удовлетворяют некоторым простым соотношениям, о ...
... {ξn (ω )}¥n=1 . Поэтому, во-первых, можно говорить о знакомой из математического анализа (почти) поточечной сходимости последовательностей функций: о сходимости «почти всюду», которую в теории вероятностей называют сходимостью «почти наверное». Определение 46. Говорят, что последовательность с. в. {ξn } сходится почти наверное к с. в. ξ при n ® ¥ , и пишут: ξn ...
... ничего другого, кроме как опять же события и . Действительно, имеем: *=, *=, =, =. Другим примером алгебры событий L является совокупность из четырех событий: . В самом деле: *=,*=,=,. 2.Вероятность. Теория вероятностей изучает случайные события. Это значит, что до определенного момента времени, вообще говоря, нельзя сказать заранее о случайном событии А произойдет это событие или нет. Только ...
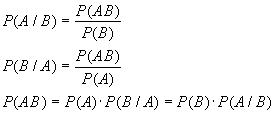
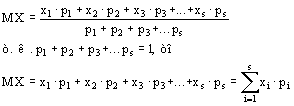
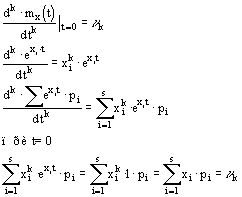
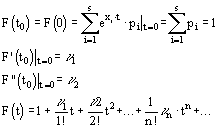
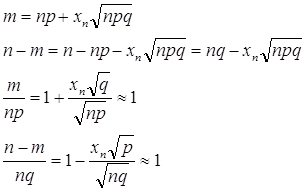
0 комментариев