Навигация
Постоянный множитель можно выносить за знак интеграла, то есть
1. Постоянный множитель можно выносить за знак интеграла, то есть
 ,
,
где ![]()
![]() – некоторое число.
– некоторое число.
2. Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций, то есть
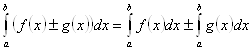 .
.
3. Если отрезок интегрирования разбит на части, то интеграл на всем отрезке равен сумме интегралов для каждой из возникших частей, то есть при любых ![]()
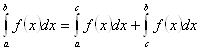
4. Если на отрезке ![]() , где
, где ![]() ,
, ![]() , то и
, то и
 .
.
Следствие. Пусть на отрезке ![]() , где
, где ![]() ,
, ![]() , где
, где ![]() и
и ![]() – некоторые числа. Тогда
– некоторые числа. Тогда
 .
.
Теорема о среднем. Если функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() , где
, где ![]() , то найдется такое значение
, то найдется такое значение ![]() , что
, что
 .
.
Теорема. Пусть функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() и
и ![]() – любая первообразная для
– любая первообразная для ![]() на
на ![]() . Тогда определенный интеграл от функции
. Тогда определенный интеграл от функции ![]() на
на ![]() равен приращению первообразной на
равен приращению первообразной на ![]() на этом отрезке, то есть
на этом отрезке, то есть
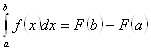
Эта формула называется формулой Ньютона – Лейбница.
Теорема. Пусть функция ![]() имеет непрерывную производную на отрезке
имеет непрерывную производную на отрезке ![]() ,
, ![]() и функция
и функция ![]() непрерывна в каждой точке
непрерывна в каждой точке ![]() вида
вида ![]() , где
, где ![]() .
.
Тогда имеет место равенство
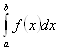 =
= .
.
Эта формула носит название формулы замены переменной в определенном интеграле.
Теорема. Пусть функции ![]() и
и ![]() имеют непрерывные производные на отрезке
имеют непрерывные производные на отрезке ![]() . Тогда
. Тогда
 .
.
Эта формула называется формулой интегрирования по частям.
Теорема. Пусть на отрезке ![]() заданы непрерывные функции
заданы непрерывные функции ![]() и
и ![]() такие, что
такие, что ![]() . Тогда площадь
. Тогда площадь ![]() фигуры, заключенной между кривыми
фигуры, заключенной между кривыми ![]() и
и ![]() , на отрезке
, на отрезке ![]() вычисляется по формуле
вычисляется по формуле

Пусть на отрезке ![]() задана непрерывная знакопостоянная функция
задана непрерывная знакопостоянная функция ![]() . Тогда объем
. Тогда объем ![]() тела, образованного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями
тела, образованного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями ![]() ,
, ![]() и
и ![]() находится по формуле
находится по формуле
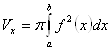 .
.
Дифференциальным уравнением называется уравнение, связывающее искомую функцию одной или нескольких переменных, эти переменные и производные различных порядков данной функции.
Дифференциальное уравнение ![]() го порядка называется разрешенным относительно старшей производной, если оно имеет вид
го порядка называется разрешенным относительно старшей производной, если оно имеет вид
![]() .
.
Решением дифференциального уравнение называется такая функция ![]() , которая при подстановке ее в это уравнение обращает его тождество.
, которая при подстановке ее в это уравнение обращает его тождество.
Общим решением дифференциального уравнения ![]() го порядка называется такое его решение
го порядка называется такое его решение
![]() ,
,
которое является функцией переменных ![]() и
и ![]() произвольных независимых постоянных
произвольных независимых постоянных ![]() .
.
Частным решением дифференциального уравнения называется решение, получаемое из общего решения при некоторых конкретных числовых значениях постоянных ![]() .
.
Теорема. Пусть в дифференциальном уравнении
![]() (1)
(1)
функция ![]() и ее частная производная
и ее частная производная ![]() непрерывны на открытом множестве
непрерывны на открытом множестве ![]() координатной плоскости. Тогда
координатной плоскости. Тогда
1. Для любой точки ![]() множества
множества ![]() найдется решение
найдется решение ![]() уравнения (1), удовлетворяющее условию
уравнения (1), удовлетворяющее условию ![]() .
.
2. Если два решения ![]() и
и ![]() уравнения (1) совпадают хотя бы для одного значения
уравнения (1) совпадают хотя бы для одного значения ![]() , то эти решения совпадают для всех тех значений переменной
, то эти решения совпадают для всех тех значений переменной ![]() , для которых они определены.
, для которых они определены.
Дифференциальное уравнение (1) первого порядка называется неполным, если функция ![]() явно зависит либо только от
явно зависит либо только от![]() , либо только от
, либо только от ![]() .
.
Дифференциальное уравнение первого порядка называется уравнением с разделяющимися переменными, если оно может быть представлено в виде
![]()
или в виде
![]() ,
,
где ![]() ,
, ![]() ,
, ![]() – некоторые функции переменной
– некоторые функции переменной ![]() ;
; ![]() – функции переменной
– функции переменной ![]() .
.
Дифференциальное уравнение первого порядка называется линейным, если оно имеет вид
![]() ,
,
где ![]() и
и ![]() – некоторые (непрерывные) функции переменной
– некоторые (непрерывные) функции переменной ![]() .
.
В случае, когда функция ![]() тождественно равна нулю, уравнение называется однородным, в противном случае – неоднородным.
тождественно равна нулю, уравнение называется однородным, в противном случае – неоднородным.
Линейное дифференциальное уравнение второго порядка с постоянными коэффициентами имеет вид
![]() , (2)
, (2)
где ![]() – некоторые действительные числа,
– некоторые действительные числа, ![]() – некоторая функция.
– некоторая функция.
Если ![]() , то уравнение
, то уравнение
![]() (3)
(3)
называется однородным, в противном случае при![]() уравнение (2) называется неоднородным.
уравнение (2) называется неоднородным.
Теорема. Если ![]() и
и ![]() – линейно независимые частные решения уравнения (3), то общее решение этого уравнения является линейной комбинацией этих частных решений, то есть имеет вид
– линейно независимые частные решения уравнения (3), то общее решение этого уравнения является линейной комбинацией этих частных решений, то есть имеет вид
![]() ,
,
Для некоторых действительных чисел ![]() и
и ![]() .
.
Уравнение
![]() (4)
(4)
называется характеристическим уравнением уравнения (3).
Теорема.
1. Пусть характеристическое уравнение (4) имеет действительные корни ![]() , причем
, причем ![]() . Тогда общее решение уравнения (3) имеет вид
. Тогда общее решение уравнения (3) имеет вид
![]() ,
,
где ![]() и
и ![]() – некоторые числа.
– некоторые числа.
2. Если характеристическое уравнение (4) имеет один корень ![]() (кратности 2), то общее уравнения (3) имеет вид
(кратности 2), то общее уравнения (3) имеет вид
![]() ,
,
где ![]() и
и ![]() – некоторые числа.
– некоторые числа.
Похожие работы
... условий: y(x0)=y0, . Эти начальные условия дают соответственно n уравнений , , , ……………………………… , решая которые относительно c1, c2 , …, cn находят значения этих постоянных. Например, для дифференциального уравнения 1-го порядка общее решение имеет вид y=f(x,c). Тогда начальное условие y(x0)=y0 выделяет из всего семейства интегральных кривых кривую, проходящую через точку M(x0,y0). Геометрическая ...
виде . Определение Д.у. первого порядка называется однородным, если оно может быть представлено в виде . (Для решения используется замена t=y/x)/ Определение Дифференциальное уравнение первого порядка называется линейным, если оно имеет вид (линейное неоднородное). (Сначала решаем уравнение - линейное однородное, находим y и подставляем в исходное). Определение Уравнение вида ...
... коэффициенты an (x1), bn (x1), an (x2), bn (x2) при помощи гармонического анализа, можно определить коэффициент температуропроводности стержня а2. Глава 3. МОДЕЛИРОВАНИЕ С ПОМОЩЬЮ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ. §3.1. Дифракция излучения на сферической частице. Перейдем теперь к рассмотрению задачи о дифракции электромагнитных волн на сферической частице. Как известно, в ...
... в начальный момент (t=0). Совокупность граничных и начальных условий называется краевыми условиями: 2.2. Формула Даламбера. Изучение методов построения решений краевых задач для уравнений гиперболического типа начнем с задачи с начальными условиями для неограниченной струны: (2) (3) Преобразуем это уравнение к каноническому виду, содержащему смешанную производную. Уравнение характеристик ...
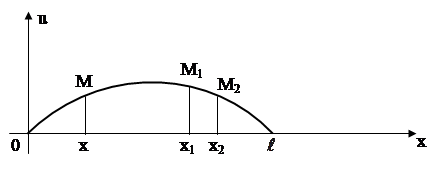
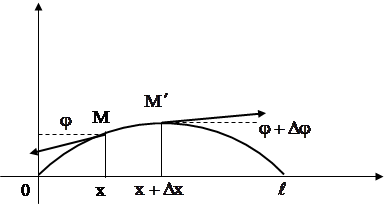
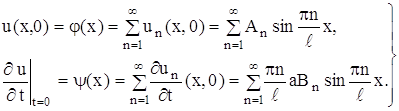

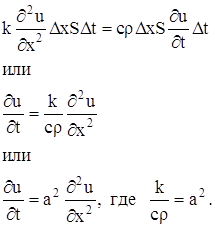
0 комментариев