Навигация
Дифференциальные уравнения гиперболического типа
Курсовая работа студента гр. МТ-31 Нургалиев А.
Инновационный евразийский университет
Павлодар 2007 год.
1. Введение.Многие задачи математической физике приводят к дифференциальным уравнениям с частными производными. В настоящей курсовой работе рассмотрены одни из основных уравнений гиперболического типа: 4-го и наиболее часто встречающегося 2-го порядка.
Рассмотрено простейшее уравнение гиперболического типа – волновое уравнение. К исследованию этого уравнения приводят рассмотрение процессов поперечных колебаний струны, продольных колебаний стержня, электрических колебаний в проводе, крутильных колебаний вала, колебаний газа и т. д. Приведена формула Даламбера для решения краевых задач, а также её физическая интерпретация.
Большое число задач о колебаниях стержней, пластин и т.д. приводит к уравнениям более высокого порядка. В качестве примера на уравнения 4-го порядка рассмотрена задача о собственных колебаниях камертона.
2. Метод распространяющихся волн.
2.1. Вывод уравнения колебаний струны.
В математической физике под струной понимают гибкую, упругую нить. Напряжения, возникающие в струне в любой момент времени направлены по касательной к ее профилю. Пусть струна длины l в начальный момент направлена по отрезку оси 0x от 0 до l. Предположим, что концы струны закреплены в точках x=0 и x=l. Если струну отклонить от ее первоначального положения, а потом предоставить самой себе или, не отклоняя струны, придать в начальный момент ее точкам некоторую скорость, или отклонить струну и придать ее точкам некоторую скорость, то точки струны будут совершать движения – говорят, струна начнет колебаться. Задача заключается в определении формы струны в любой момент времени и определении закона движения каждой точки струны в зависимости от времени.
Будем рассматривать малые отклонения точек струны от начального положения. В силу этого можно предполагать, что движение точек струны происходит перпендикулярно оси 0x и в одной плоскости. При этом предположении процесс колебания струны описывается одной функцией u(x,t) которая дает величину перемещения точки струны с абсциссой x в момент t.
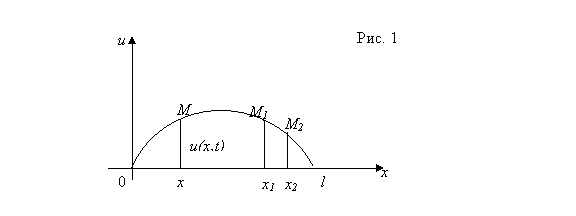
Так как мы рассматриваем малые отклонения точек струны в плоскости (x,u), то будем предполагать, что длина элемента струны M1M2 равняется ее проекции на ось 0x, т.е. M1M2=x2-x1. Также будем предполагать, что натяжение во всех точках струны одинаковое; обозначим его через T.
Рассмотрим элемент струны MM’.
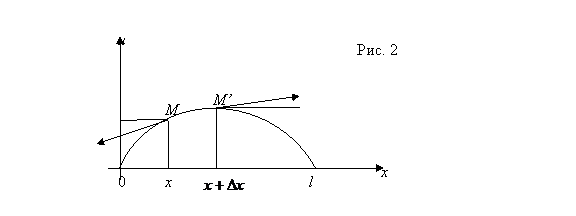
На концах этого элемента, по касательным к струне, действуют силы T. Пусть касательные образуют осью 0x углы ![]() и
и ![]() . Тогда проекция на ось 0u сил, действующих на элемент MM’, будет равна
. Тогда проекция на ось 0u сил, действующих на элемент MM’, будет равна ![]() . Так как угол
. Так как угол ![]() мал, то можно положить
мал, то можно положить ![]() , и мы будем иметь:
, и мы будем иметь:
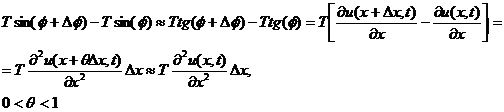
(здесь мы применили теорему Лагранжа к выражению, стоящему в квадратных скобках).
Чтобы получить уравнение движения, нужно внешние силы, приложенные к элементу, приравнять силе инерции. Пусть масса элемента струны будет ![]() . Ускорение элемента равно
. Ускорение элемента равно ![]() . Следовательно, по принципу Даламбера будем иметь:
. Следовательно, по принципу Даламбера будем иметь:
![]()
Сокращая на ![]() и обозначая
и обозначая ![]() , получаем уравнение движения
, получаем уравнение движения
![]() (1)
(1)
Это и есть волновое уравнение – уравнение колебания струны. Для полного определения движения струны одного уравнения (1) недостаточно. Искомая функция u(x,t) должна удовлетворять еще граничным условия, указывающим, что делается на концах струны (x=0 и x=l), и начальным условиям, описывающим состояние струны в начальный момент (t=0). Совокупность граничных и начальных условий называется краевыми условиями:
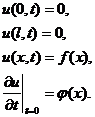
Похожие работы
... коэффициенты an (x1), bn (x1), an (x2), bn (x2) при помощи гармонического анализа, можно определить коэффициент температуропроводности стержня а2. Глава 3. МОДЕЛИРОВАНИЕ С ПОМОЩЬЮ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ. §3.1. Дифракция излучения на сферической частице. Перейдем теперь к рассмотрению задачи о дифракции электромагнитных волн на сферической частице. Как известно, в ...
... менять саму их постановку, вводя в нее дополнительную априорную информацию о строении решения. 2. Классификация уравнений гиперболического типа в контексте классификации уравнений математической физики Уравнения математической физики, дифференциальные уравнения с частными производными, а также некоторые родственные уравнения иных типов (интегральные, интегро-дифференциальные ...
... Дис-петчер 1.1 3 Рис. 5. HIPO-диаграмма. Задание к лабораторной работе С помощью HIPO-технологии составить внешние спецификации для комплекса программ решения одной из следующих задач. 1.Численное решение задачи Коши для дифференциального уравнения методом Рунге-Кутта и Адамса с автоматическим выбором шага и заданным шагом. 2.Интерполирование табличной функции. 3.Численное ...
... была построена теория вложения функциональных пространств, которые в настоящее время носят название пространств Соболева. А.Н. Тихоновым была построена теория некорректных задач. Выдающийся вклад в современную теорию дифференциальных уравнений внесли российские математики Н.Н. Боголюбов, А.Н. Колмогоров, И.Г. Петровский, Л.С. Понтрягин, С.Л. Соболев, А.Н. Тихонов и другие. Влияние на развитие ...
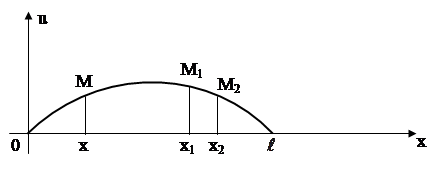
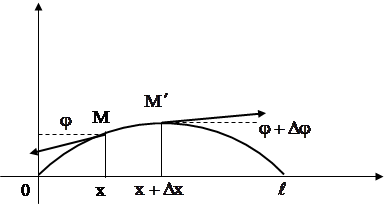
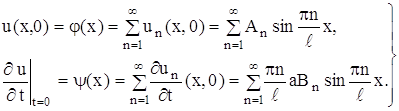

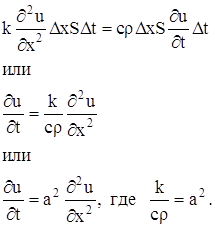

0 комментариев