Навигация
Интегралы. Дифференциальные уравнения
Интегралы
Основные вопросы лекции: первообразная; неопределенный интеграл, его свойства; таблица интегралов; методы интегрирования: разложение, замена переменной, по частям; интегрирование рациональных функций; интегрирование иррациональностей и выражений, содержащих тригонометрические функции, задачи, приводящие к понятию определенного интеграла; интегральная сумма; понятие определенного интеграла, его свойства; определенный интеграл как функция верхнего предела; формула Ньютона Лейбница; применение определенного интеграла к вычислению площадей плоских фигур; вычисление объемов тел и длин дуг кривых; несобственные интегралы с бесконечными пределами и от неограниченных функций, основные понятия дифференциальных уравнений; задача Коши; дифференциальные уравнения с разделяющимися переменными; однородные дифференциальные уравнения 1-го порядка; линейные дифференциальные уравнения 1-го порядка, дифференциальные уравнения 2-го порядка, допускающие понижение порядка; линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами: однородные и неоднородные.
Функция ![]() называется первообразной для функции
называется первообразной для функции ![]() на промежутке
на промежутке ![]() , если в любой точке этого промежутка
, если в любой точке этого промежутка ![]() .
.
Теорема. Если ![]() и
и ![]() – первообразные для функции
– первообразные для функции ![]() на некотором промежутке
на некотором промежутке ![]() , то найдется такое число
, то найдется такое число ![]() , что будет справедливо равенство
, что будет справедливо равенство
![]() =
= ![]() +
+ ![]() .
.
Множество всех первообразных для функции ![]() на промежутке
на промежутке![]() называется неопределенным интегралом от функции
называется неопределенным интегралом от функции![]() и обозначается
и обозначается ![]() . Таким образом,
. Таким образом,
![]() =
= ![]() +
+ ![]() .
.
Свойства неопределенного интеграла
1. Производная от неопределенного интеграла равна подынтегральной функции, то есть
![]() .
.
2. Дифференциал неопределенного интеграла равен подынтегральному выражению, то есть
![]()
3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого, то есть
![]() ,
,
где ![]() – произвольное число.
– произвольное число.
4. Постоянный множитель можно выносить за знак интеграла, то есть
![]()
5. Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций, то есть
![]() .
.
Метод замены переменной
![]() ,
,
где ![]() – функция, дифференцируемая на рассматриваемом промежутке.
– функция, дифференцируемая на рассматриваемом промежутке.
Метод интегрирования по частям
![]() ,
,
где ![]() и
и ![]() – дифференцируемые функции.
– дифференцируемые функции.
Интегрирование рациональных дробей. Простейшими дробями называют дроби вида
![]() и
и ![]() ,
,
причем квадратный трехчлен не имеет действительных корней.
Рациональную функцию ![]() можно разложить в сумму простейших дробей, причем в знаменателе этих дробей могут быть и степени от выражения стоящего в знаменателе.
можно разложить в сумму простейших дробей, причем в знаменателе этих дробей могут быть и степени от выражения стоящего в знаменателе.
Для интегралов вида ![]() делают замену
делают замену ![]() , а для интегралов
, а для интегралов ![]() в общем случае используются подстановки Эйлера.
в общем случае используются подстановки Эйлера.
При интегрировании тригонометрических выражений ![]() в общем случае используется замена переменной
в общем случае используется замена переменной ![]() , где
, где ![]() .
.

![]()
Талица основных интегралов.
1. ![]()
![]()
2. ![]()
3. ![]()
4. ![]()
5. ![]()
6. ![]()
7. ![]()
8. ![]()
9. ![]()
10. ![]()
11. ![]()
12. ![]()
Пусть на отрезке ![]() задана функция
задана функция ![]() . Разобьем отрезок
. Разобьем отрезок ![]() на
на![]() элементарных отрезков точками
элементарных отрезков точками ![]()
![]() . На каждом отрезке
. На каждом отрезке ![]() разбиения выберем некоторую точку
разбиения выберем некоторую точку ![]() и положим
и положим ![]() , где
, где ![]() . Сумму вида
. Сумму вида
![]() (1)
(1)
будем называть интегральной суммой для функции ![]() .на
.на ![]() . Для избранного разбиения отрезка
. Для избранного разбиения отрезка ![]() на части обозначим через
на части обозначим через ![]() максимальную из длин отрезков
максимальную из длин отрезков ![]() , где
, где ![]() .
.
Пусть предел интегральной суммы при стремлении ![]() к нулю существует, конечен и не зависит от способа выбора точек
к нулю существует, конечен и не зависит от способа выбора точек ![]() и точек
и точек ![]() . Тогда этот предел называется определенным интегралом от функции
. Тогда этот предел называется определенным интегралом от функции ![]() на
на![]() , обозначается
, обозначается 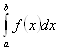 , а сама функция
, а сама функция ![]() называется интегрируемой на отрезке
называется интегрируемой на отрезке ![]() , то есть
, то есть
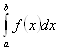 =
= ![]()
![]() .
.
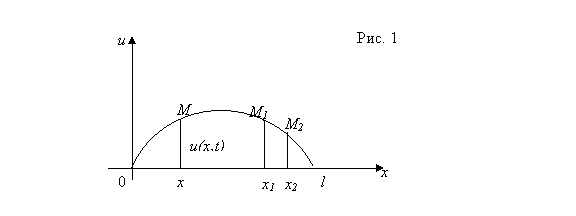
Экономический смысл интеграла. Если ![]() – производительность труда в момент времени
– производительность труда в момент времени ![]() , то
, то 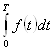 есть объем выпускаемой продукции за промежуток
есть объем выпускаемой продукции за промежуток ![]() . Величина и объем продукции, произведенной за промежуток времени
. Величина и объем продукции, произведенной за промежуток времени ![]() , численно равна площади под графиком функции
, численно равна площади под графиком функции ![]() , описывающей изменение производительности труда с течением времени, на промежутке
, описывающей изменение производительности труда с течением времени, на промежутке ![]() или
или 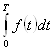 .
.
Достаточное условие существования интеграла. Теорема. Если ![]() непрерывна на отрезке
непрерывна на отрезке ![]() , то она интегрируема на этом отрезке.
, то она интегрируема на этом отрезке.
Свойства определенного интеграла.
Похожие работы
... условий: y(x0)=y0, . Эти начальные условия дают соответственно n уравнений , , , ……………………………… , решая которые относительно c1, c2 , …, cn находят значения этих постоянных. Например, для дифференциального уравнения 1-го порядка общее решение имеет вид y=f(x,c). Тогда начальное условие y(x0)=y0 выделяет из всего семейства интегральных кривых кривую, проходящую через точку M(x0,y0). Геометрическая ...
виде . Определение Д.у. первого порядка называется однородным, если оно может быть представлено в виде . (Для решения используется замена t=y/x)/ Определение Дифференциальное уравнение первого порядка называется линейным, если оно имеет вид (линейное неоднородное). (Сначала решаем уравнение - линейное однородное, находим y и подставляем в исходное). Определение Уравнение вида ...
... коэффициенты an (x1), bn (x1), an (x2), bn (x2) при помощи гармонического анализа, можно определить коэффициент температуропроводности стержня а2. Глава 3. МОДЕЛИРОВАНИЕ С ПОМОЩЬЮ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ. §3.1. Дифракция излучения на сферической частице. Перейдем теперь к рассмотрению задачи о дифракции электромагнитных волн на сферической частице. Как известно, в ...
... в начальный момент (t=0). Совокупность граничных и начальных условий называется краевыми условиями: 2.2. Формула Даламбера. Изучение методов построения решений краевых задач для уравнений гиперболического типа начнем с задачи с начальными условиями для неограниченной струны: (2) (3) Преобразуем это уравнение к каноническому виду, содержащему смешанную производную. Уравнение характеристик ...
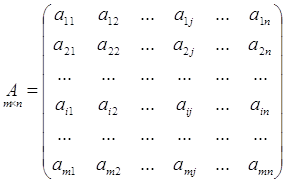
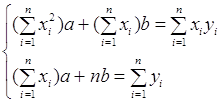
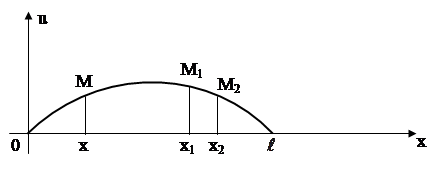
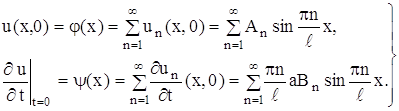

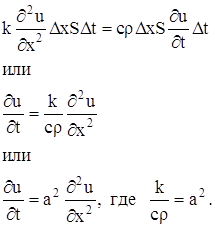
0 комментариев