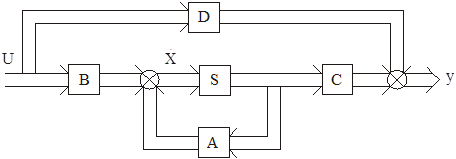
Математическая модель системы в переменных пространства состояний имеет вид
![]() , (2.1.1)
, (2.1.1)
![]() (2.1.2)
(2.1.2)
где ![]() мерный вектор параметров состояний;
мерный вектор параметров состояний; ![]() мерный вектор управляющих воздействий;
мерный вектор управляющих воздействий; ![]() мерный вектор возмущающих воздействий;
мерный вектор возмущающих воздействий; ![]() l- мерный вектор выходов; А – матрица состояний системы размерности
l- мерный вектор выходов; А – матрица состояний системы размерности ![]() ; В – матрица управлений размерности
; В – матрица управлений размерности ![]() ; Г – матрица возмущений размерности
; Г – матрица возмущений размерности ![]() ; С – матрица выходов размерности l
; С – матрица выходов размерности l![]() n; D – матрица компенсаций (обходов) размерности l
n; D – матрица компенсаций (обходов) размерности l![]() m.
m.
Решение векторного дифференциального уравнения (2.1.1) имеет следующий вид:
 , (2.1.3)
, (2.1.3)
где ![]() - экспоненциал матрицы А.
- экспоненциал матрицы А.
Подставляя выражение (2.1.3) в формулу (2.1.2), получаем интегральное уравнение движения системы в переменных «вход – выход».
Рассмотрение движения системы в переменных пространства состояний связано с трудностью решения дифференциальных уравнений n-го порядка, описывающих движение системы в переменных «вход – выход», и с хорошо разработанными методами решения систем дифференциальных уравнений первого порядка.
2.2. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 2.2.1Определить переходные процессы в системе
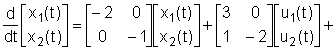
 (2.2.1)
(2.2.1)
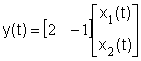 , (2.2.2)
, (2.2.2)
под действием ступенчатых воздействий по каналам управления
 и возмущения
и возмущения 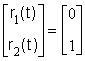 .
.
В соответствии с выражениями (2.1.2), (2.1.3) запишем уравнение движения системы в интегральной форме
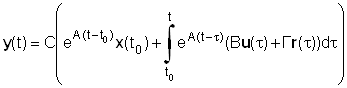 . (2.2.3)
. (2.2.3)
Учитывая, что u(t)=u*1(t)=u, r(t)=r*1(t)=r и t0=0, представим выражение (2.2.3) в виде
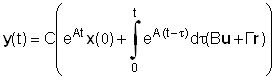 . (2.2.4)
. (2.2.4)
Для нахождения экспоненциала матрицы А определим корни характеристического уравнения ![]() , то есть
, то есть
 и
и ![]() .
.
Так как корни различные действительные и матрица А диагональная, то ее экспоненциал равен
 . (2.2.5)
. (2.2.5)
Подставляя выражения (2.2.5) в формулу (2.2.4) и последовательно проводя преобразования, получаем


![]()
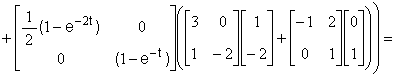
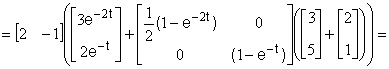
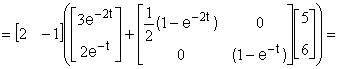

=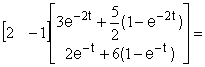
![]() .
.
Следовательно, уравнение движения рассматриваемой системы в переменных «вход – выход» имеет вид:
![]() .
.
УСТОЙЧИВОСТЬ
ОСНОВНЫЕ ПОНЯТИЯ И РАСЧЕТНЫЕ ФОРМУЛЫУстойчивость или неустойчивость линейной многомерной системы (2.1.1) определяется ее свободным движением (![]()
![]() ), которое характеризуется собственными числами матрицы А, определяемыми из характеристического уравнения
), которое характеризуется собственными числами матрицы А, определяемыми из характеристического уравнения
![]() (3.1.1)
(3.1.1)
Линейная система (2.1.1) устойчива тогда и только тогда, когда все вещественные части собственных (характеристических) чисел λj=λj(A) (j=1,…,n) имеют неположительные значения, т.е. Reλj![]() . Если Reλj<0, то система асимптотически устойчива.
. Если Reλj<0, то система асимптотически устойчива.
Характеристическое уравнение (3.1.1) можно записать в виде
nn-1nn0. (3.1.2)
Условия устойчивости для системы n-го порядка записываются в виде определителей Гурвица, получаемых из квадратной матрицы коэффициентов характеристического уравнения (3.1.2).
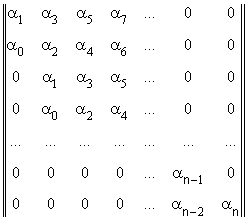 .
.
Для устойчивости линейной системы по критерию Гурвица необходимо и достаточно, чтобы при α0>0 были положительными и все n диагональных определителей Гурвица, то есть ΔI>0 (i=l,...,n). Положительность последнего определителя Гурвица
Δn=αnΔn-1 (3.1.3)
при Δn-1>0 сводится к положительности свободного члена αn характеристического уравнения.
3.2. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ Задача 3.2.1Определить устойчивость и характер свободного движения динамической системы, заданной в пространстве состояний векторными уравнениями
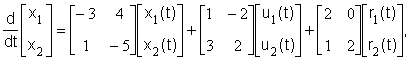
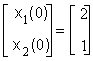 , (3.2.1)
, (3.2.1)
 . (3.2.2)
. (3.2.2)
Решение.
Запишем для системы (3.2.1) характеристическое уравнение (3.1.1)

![]() , (3.2.3)
, (3.2.3)
решение которого дает следующие корни:
![]() .
.
Рассматриваемая динамическая система является устойчивой. Ее свободное движение носит апериодический сходящийся характер, так как вещественные части корней характеристического уравнения отрицательные.
Задача 3.2.2Определить устойчивость динамической системы, заданной в пространстве состояний векторно-матричными уравнениями

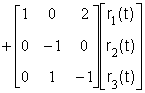 ,
, 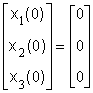 , (3.2.4)
, (3.2.4)
 . (3.2.5)
. (3.2.5)
Решение.
Запишем для системы (3.2.4) характеристическое уравнение (3.1.1)

![]() . (3.2.6)
. (3.2.6)
Раскроем скобки и приведем подобные члены, получим следующее характеристическое уравнение:
![]() . (3.2.7)
. (3.2.7)
Устойчивость системы будем определять на основе алгебраического критерия устойчивости Гурвица, составив для этого по уравнению (3.2.7) матрицу Гурвица
 . (3.2.8)
. (3.2.8)
Для устойчивости линейной системы по критерию Гурвица необходимо и достаточно, чтобы при положительности коэффициента при старшей степени (в нашем случае коэффициент при λ3 равен 1) были положительными и все n диагональных определителей Гурвица, то есть Δi>0 (i=1,2,3)
![]() ,
,  .
.
В соответствии с вышеизложенным находим, что свободный член характеристического уравнения (3.2.7) равный 54 - положительный.
Следовательно, система (3.2.4) является устойчивой.
УПРАВЛЯЕМОСТЬ
ОСНОВНЫЕ ПОНЯТИЯ И РАСЧЕТНЫЕ ФОРМУЛЫ
Управляемость системы (2.1.1), (2.1.2) по состояниям определяется теоремой (критерием) Калмана: система будет управляемой тогда и только тогда, когда ранг матрицы управляемости Lc размерности ![]() равен n, то есть
равен n, то есть
rank![]() n, (4.1.1)
n, (4.1.1)
где
![]() . (4.1.2)
. (4.1.2)
Если rank![]() <n, то система будет частично управляемой, а при rank
<n, то система будет частично управляемой, а при rank![]() =0 – полностью неуправляемой.
=0 – полностью неуправляемой.
Управляемость системы (2.1.1), (2.1.2) по выходам (критерий Калмана): система будет управляемой тогда и только тогда, когда ранг матрицы управляемости ![]() размерности
размерности ![]() равен l то есть
равен l то есть
rank![]() =l, (4.1.3)
=l, (4.1.3)
где
![]() . (4.1.4)
. (4.1.4)
Если rank![]() <l, то система будет частично управляемой по выходам, а при rank
<l, то система будет частично управляемой по выходам, а при rank![]() =0 – полностью неуправляемой.
=0 – полностью неуправляемой.
Показатель степени n в выражениях (4.1.2), (4.1.4) соответствует размерности вектора состояний.
4.2. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 4.2.1Определить управляемость динамической системы по состояниям, заданной векторными уравнениями
 ,
,
(4.2.1)
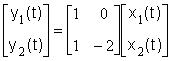 . (4.2.2)
. (4.2.2)
Решение.
В соответствии с выражением (4.1.2) запишем матрицу управляемости для n=2, так как в рассматриваемом случае размерность вектора состояний n=2
![]() .
.
Найдем произведение матриц
 .
.
Следовательно, матрица управляемости имеет вид
 ,
,
и ее ранг rank![]() 2, то есть настоящая система полностью управляема по состояниям.
2, то есть настоящая система полностью управляема по состояниям.
Определить управляемость по выходам динамической системы, заданной векторными уравнениями
 ,
,
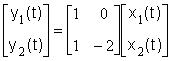 .
.
Решение.
В соответствии с выражением (4.1.2) запишем матрицу управляемости для n=2, так как в рассматриваемом случае размерность вектора состояний n=2
![]() .
.
Найдем произведение матриц
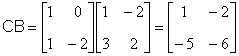 .
.
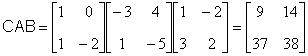 .
.
Следовательно, матрица управляемости имеет вид
 ,
,
и ее ранг rank![]() =2, то есть настоящая система полностью управляема по выходам.
=2, то есть настоящая система полностью управляема по выходам.
5. НАБЛЮДАЕМОСТЬ
5.1. ОСНОВНЫЕ ПОНЯТИЯ И РАСЧЕТНЫЕ ФОРМУЛЫ
Наблюдаемость системы (2.1.1), (2.1.2) определяется теоремой (критерием) Калмана: система будет вполне наблюдаемой тогда и только тогда, когда ранг матрицы наблюдаемости L0 размерности ![]() равен n, то есть
равен n, то есть
rank![]() n, (5.1.1)
n, (5.1.1)
где
 . (5.1.2)
. (5.1.2)
Если rank![]() <n, то система будет не вполне наблюдаемой, а при rank
<n, то система будет не вполне наблюдаемой, а при rank![]() =0 – полностью ненаблюдаемой.
=0 – полностью ненаблюдаемой.
Определить наблюдаемость динамической системы, заданной векторными уравнениями

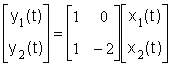 .
.
Решение.
В соответствии с выражением (5.1.2) запишем матрицу наблюдаемости для n=2, так как в рассматриваемом случае размерность вектора состояний n=2
![]() .
.
Найдем произведение матриц

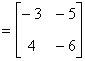 .
.
Следовательно, матрица наблюдаемости имеет вид
 ,
,
и ее ранг rank![]() 2, то есть настоящая система полностью наблюдаема.
2, то есть настоящая система полностью наблюдаема.
Похожие работы
... проектирования. Целью проекта является создание программного продукта (ПП), основанного на математическом пакете MatLab, реализующего математическую модель системы управления, построенной на основе оптимального закона, для системы слежения РЛС. Данный проект можно отнести к научно-исследовательской работе, которая принадлежит к типу прикладных, направленных на решение научных проблем с целью ...
... и ФЧХ. 3) Проанализировать зависимость вида переходного процесса от параметров схемы. 2. Расчет переходного процесса на основе численных методов решения дифференциальных уравнений 2.1 Разработка математической модели и её решение с использованием метода пространства состояний При рассмотрении физической системы как объекта исследования или проектирования целесообразно распределить все ...
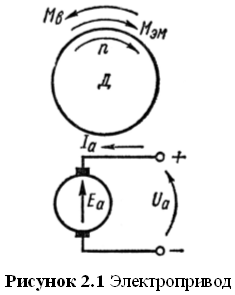
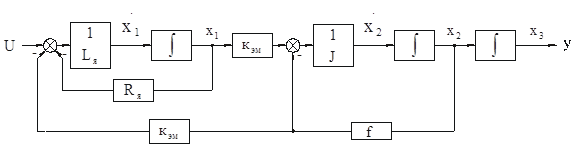
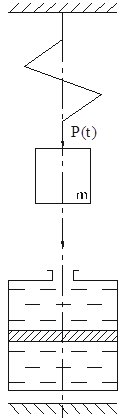
... . Рассмотрим структурную схему электромеханической системы с двигателем постоянного тока, работающего на инерционную нагрузку с вязким трением. Рис. 2.1. Структурная схема электромеханической системы с двигателем постоянного тока Запишем уравнение состояния для механической системы, представляющей собой груз массой m, подвешенный на пружине и соединенный с гидравлическим демпфером. К ...
... . В результате, на выходе реле сигнал будет непрерывным, но ступенчатым 3.2.2.3 Релейно-импульсные системы В них происходит квантование сигналов по времени и по уровню. К этому типу относятся цифровые системы управления, в частности АСУТП с используемым ВК. При большом количестве разрядов АЦП и ЦАП квантованием можно пренебречь, и отнести такие системы к импульсным. 3.2.2.4 Системы на ...



0 комментариев