Навигация
5.3. Урок-мастерская
Урок-мастерская нацеливает учащихся на то, чтобы они собственным трудом добывали знания. В этом - основной лейтмотив развивающей педагогики. Тема «Степенная функция» очень подходит для творческой работы всего класса, так как степенная функция (у = хn, где n — любое рациональное число) — это фактически множество функций, имеющих различные свойства в зависимости от показателя степени.
Обсуждение этих свойств лучше всего организовать по группам. Для этого класс целесообразно поделить на шесть групп.
Прежде всего, учителю необходимо представлять себе последовательность работы в «мастерской»:
I этап - индукция - обращение к предыдущему опыту;
II этап — обсуждение темы в группах, а далее со всем классом;
III этап - разрыв - момент, когда учащиеся должны осознать, что в их знаниях имеются пробелы, которые они сами должны восполнить;
IV этап — рефлексия — определение степени усвоения.
Опишем подробнее каждый из этапов урока.
I этап — индукция. Учитель напоминает о том, что в классе уже изучат функции у=х, у=![]() , у=x2 их свойства и графики. Эти функции можно в общем виде задать формулой: у=хq, где q — некоторое целое число. Такая функция называется степенной. Перед классом ставится следующая задача: перечислить вопросы, на которые мы должны ответить, изучая новую функцию.
, у=x2 их свойства и графики. Эти функции можно в общем виде задать формулой: у=хq, где q — некоторое целое число. Такая функция называется степенной. Перед классом ставится следующая задача: перечислить вопросы, на которые мы должны ответить, изучая новую функцию.
Класс обсуждает эти вопросы по группам, а потом все вопросы от групп собираются в единый список:
- Какими свойствами обладает данная функция?
- Каков ее график?
- В каких ситуациях она используется?
Начнем с ответа на последний вопрос. Приведем примеры нескольких ситуаций, в которых появляется степенная функция.
Три ученика поочередно выходят к доске и делают сообщения, подготовленные дома.
Первый ученик рассматривает функцию
S =![]() , где S - площадь поперечного сечения провода диаметром d. Слушатели замечают, что эта степенная функция фактически представляет собой квадратичную, но с ограничениями на значение аргумента d.
, где S - площадь поперечного сечения провода диаметром d. Слушатели замечают, что эта степенная функция фактически представляет собой квадратичную, но с ограничениями на значение аргумента d.
Второй ученик рассказывает о том, что сила притяжения F двух тел с массами m1, и m2, выражается формулой F=γm1m2r-2. Это функция расстояния г между этими телами. В классе найдется ученик, который заметит, что мы уже строили график функции такого вида, хотя специально ее не изучали.
Третий ученик анализирует дальность d расстояния горизонта от наблюдателя: d=3,8h1/2. Эта функция высоты, на которую поднят наблюдатель над уровнем моря. Если ребята сами этого не заметили, то учитель должен подчеркнуть, что здесь величина d не может возрастать неограниченно. Действительно, как бы ни был высоко поднят наблюдатель, он не может увидеть больше, чем позволяют возможности его зрения и выпуклость Земного шара. Этот пример особенно показателен, так как позволяет судить о целесообразности ограничений на значения функции. Здесь какие-то ограничения мы должны наложить на значения функции d, хотя значения h, теоретически говоря, могут возрастать неограниченно.
II этап - обсуждение темы. Учащимся предоставляется некоторое время для того, чтобы они разобрали свойства одной из выбранных ими степенных функций. Главная проблема здесь в выборе функции. Одна группа склонна упрощать задачу, ограничиваясь функцией вида у = х2, которая всем учащимся хорошо известна. Другая группа слишком усложняет свою работу, занявшись функцией вида y=х4 или у=х5, а то и обеими вместе, хотя общий подход к вопросу учащимся еще не ясен.
В конце концов, находятся группы, избравшие функции, графики которых уже рассматривались ранее, хотя на них не делалось нужного акцента.
Первая группа рассматривала функцию вида у=х3; отметила область ее определения: D(f)=(-∞; +∞) и нулевое значение функции при х = 0. Ребята особо остановились на том, что функция возрастает на всей области определения. Выделили промежутки, на которых функция больше или меньше нуля. Выступавшие особо подчеркнули, что эта функция нечетная и не имеет ни наибольшего, ни наименьшего значения.
От этой группы выступает перед классом один ученик, который рассказывает о результатах исследований в группе.
Вторая группа выбрала для рассмотрения функцию у=х-3. Ребята заметили, что теперь придется исключить из области определения функции число 0, т.e. D(f)=(-∞; 0) U (0; +∞). В отличие от предыдущей, эта функция не имеет нулей. Но, как и рассмотренная выше, эта функция положительна при х > 0 и отрицательна при х < 0. Она убывает на всей области определения.
Представитель этой группы особо подчеркивает различия между функциями у = х3 и у = х-3.
Еще двое учеников рассказывают о функциях у = х4; у = х-4.
Во время своих выступлений все докладчики должны продемонстрировать графики рассмотренных функций.
Во время III этапа урока учащиеся должны обобщить свои знания. А сделать это они должны самостоятельно, удивившись разнообразию рассмотренных функций. «Почему им дано одно название, если их так много и они разные?» - вот вопрос, который должны поставить перед собою учащиеся. Задача учителя — незаметно подвести учащихся к этому вопросу. Наступает момент так называемого разрыва, когда ребята должны осознать недостатки своих знаний, их ограниченность или неполноту. Действительно, одна функция из рассмотренных имеет нули, другая нет. Одна возрастает на всей области определения, другая - то возрастает, то убывает. Какую же характеристику мы должны дать всей степенной функции, чтобы она охватывала как можно больше частных случаев?
В поиске ответа на этот вопрос кто-то из ребят, в конце концов догадывается, что вид степенной функции у = хn удобно связать с четностью или нечетностью показателя степени n.
Теперь уместно снова дать задание группам обсудить свойства функций:
у = хn, где n - нечетное;
у = хn, где n — четное,
у = х-n, где n - нечетное;
у = х-n, где n - четное.
Еще раз отмечаем план исследования функции:
1. Указать область определения.
2. Определить четность или нечетность функции
(или отметить, что она не является ни четной, ни нечетной).
3. Найти нули функции, если таковые существуют.
4. Отметить промежутки знакопостоянства.
5. Найти промежутки возрастания и убывания.
6. Указать наибольшее или наименьшее значение функции.
Работа завершается тем, что на доске возникают графики рассмотренных функций (рис. 1, а-г). Эти графики выполняют представители каждой из групп.
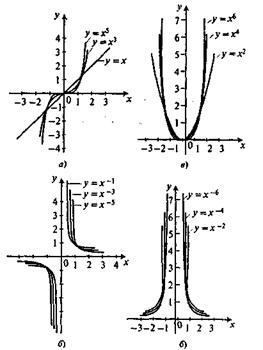
Рис. I
Теперь вместе с классом строим графики функции у = х1/n, у =x -1/n, где n - натуральное число и n ≥ 2 (рис. 2, а. 6).
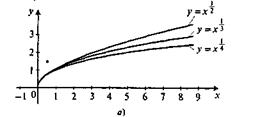
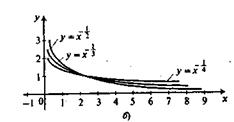
Рис. 2
Отмечается общее свойство этих функций: они обе имеют область определения - промежуток (0; +∞). Они обе являются ни четной, ни нечетной. Они обе больше нуля.
Но у этих функций есть и различия. Ребята их называют особо: функция вида у = х1/n возрастает на своей области определения, а функция вида у = х-1/n убывает на той же области. Функция вида у = х1/n имеет нулевое значение при х = 0, а функция вида у = х-1/n не имеет нулей.
На IV этапе учащиеся должны заняться рефлексией, т.е. определением степени усвоения материала. Весь класс получает следующее задание по рис. 3.
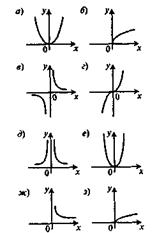
Рис. 3
На рис. 3, а-з схематически изображены графики функций, которые заданы формулами: у = х3; у = x1/3; y=x4; у = х2; у = 1/x2; у=x1/2; y = х-1, у = х-1/2.
Установите, какая формула из данного списка примерно соответствует каждому из графиков а-з.
5.4. Учебные викторины
Одной из нетрадиционных форм обучения является учебная викторина. Она нацеливает учащихся на интерес к математике, развивает их умственные способности, заставляет их мыслить нетрадиционно. Рассмотрим несколько примеров проведения математических викторин в 11 и 5 классах.
Математическая викторина 5 класс.
Математическую викторину можно провести в виде "Рыбки»
1. Из плотной цветной бумаги изготавливается несколько рыбок

2.На чистой обратной стороне пишется задача

3. К каждой рыбке прикрепляется большая железная скрепка
4. Все рыбки с задачами помещаются в ящик
5. Представители команд вылавливают рыбки из ящика с помощью удочки (палочки с веревочкой, на конце которой прикрепляется магнит)
6. Пойманные задачи решаются учениками и оцениваются баллами.
Задачи для "Рыбки"
1. В комнате четыре угла. В каждом углу сидит кошка. Против каждой кошки сидят по 3 кошки. Сколько всего кошек в комнате?
2. Сколько квадратов на чертеже?

2. Сколько треугольников на чертеже?

4. У меня в левом кармане столько же денег, сколько в правом. Из левого переложили в правый одну копейку. На сколько после этого станет больше денег в правом кармане, чем в левом?
5. Пять рыбаков за 5 часов распотрошат 5 судаков. За сколько часов 100 рыбаков распотрошат 100 судаков?
6. Что тяжелее: пуд железа или пуд пуха?
7. На озере росли лилии. Каждый день их число удваивалось и на 20-й день заросло все озеро. На какой день заросла половина озера?
8. Разделить фигуру на две равные части

9. Четыре человека обменялись рукопожатиями. Сколько всего было рукопожатий?
10. Во сколько раз уменьшится число, если от него отнять половину такого же числа?
Математическую викторину можно провести в форме «Ромашки». Для этого надо:
1. Изготовить круг из цветной плотной бумаги
2. К кругу скрепками прикрепляются разноцветные лепестки, на обратной стороне которых пишется задача
3. Ученик из команды подходит к учителю, вытаскивает лепесток, читает и решает задачу

Задачи на лепестках
1. У Андрея и Бори вместе 11 орехов. У Андрея и Вовы — 12 орехов. У Бори и Вовы — 13 орехов. Сколько всего орехов у Андрея, Бори и Вовы вместе?
2. Из чисел 21, 19, 30, 25, 3, 12, 8, 15, 6, 27 подбери такие три числа, сумма которых равна 50. .
3. Перечислить не менее 6 способов, которыми можно набрать 15 копеек.
4. Как тремя отрезками, не отрывая карандаша от бумаги, перечеркнуть все точки?
5. В семье у каждого из 6 братьев есть по сестре. Сколько детей в семье?
6. Два в квадрате 4, 3 в квадрате 9. Чему равен угол в квадрате?
7. Величина угла 30°. Чему она будет равна, если рассматривать угол в лупу с 2-кратным увеличением?
8. Сколькими нулями оканчивается произведение первых десяти натуральных чисел?
9. Кто изображен на портрете;
В семье я рос один на свете,
И это правда, до конца.
Но сын того, кто на портрете,—
Сын моего отца
(На портрете — мой отец)
10. Найти сумму натуральных чисел от 1 до 100
Учитель может задать по вопросу каждой команде
1. Шел Кондрат в Ленинград.
А навстречу 12 ребят.
У каждого по 3 лукошка.
В каждом лукошке кошка.
У каждой кошки 12 котят.
У каждого котенка в зубах по 3 мышонка.
И задумался старый Кондрат:
"Сколько мышат и котят
Ребята несут в Ленинград?"
После ответа учащихся учитель прочитает стихотворение:
"Глупый, глупый Кондрат
Он один шагал в Ленинград,
А ребята с лукошками,
С мышами и кошками
Шли навстречу ему — в Кострому!
2. Электропоезд идет с востока на запад со скоростью 60 км/ч. В этом же направлении с востока на запад дует ветер со скоростью 50 км/ч. В какую сторону отклоняется дым поезда?
(Ответ: электропоезд бездымен)
Математическая викторина «Что, Где, Когда?» 11 класс.
Г. Г Плотникова (Пермь)
Математика - царица всех наук, ее любимцем является истина, а простота и бесспорность - одеянием. Математика, которая оказала столько услуг обществу, наукам и искусству, станет также путеводной звездой человеческого разума во всех областях познания.
Ян Снядецкий
Цель викторины: воспитывать интерес к математике развивать логическое мышление и расширять кругозор.
Ход викторины; к участию в викторине, привлекаются команды учащихся 11 класса по 5 человек в каждой. В состав команды входят не обязательно хорошо успевающие по математике учащиеся, но непременно начитанные, умеющие логически мыслить ребята. Они же выбирают капитана.
В центре игрового зала располагается круглый зал с волчком, а вокруг — столы учащихся полукругом.
Руководитель мероприятия, он же ведущий, объявляет начало и конец каждого раунда, оценивает ответы, комментирует их.
По жребию капитан команды крутит волчок, и эта же команда отвечает первой.
В случае неверного ответа отвечает другая команда, а если верного ответа нет, то ответ даст ведущий.
Соревнование состоит максимально из 9 раундов. В каждом раунде знатокам предлагается вопрос, подготовленный заранее учащимися (или учителем).
После двухминутного обдумывания первая команда дает ответ. У каждой команды — эксперт. Ответы на вопросы команда дает эксперту, и после заслушанного ответа эксперты дают оценку команды. Результаты ответов фиксируются на доске. Побеждает в соревновании та команда, которая наберет большее количество очков.
Можно во время викторины проводить музыкальную паузу. Она возникает либо по указанию стрелки волчка, либо по объявлению ведущего.
В конце викторины проводится награждение победившей команды.
Вопросы к викторине
1. Какой угол между стрелками в половине десятого?
2. Кусок мыла, который лежит на вашем умывальнике, имеет форму параллелепипеда. Вы расходуете мыло равномерно, каждый день одно и то
же количество. Спустя 7 дней размеры вашего мыла уменьшились вдвое, так как мыло смылось. На сколько дней хватит этого мыла, если вы будете пользоваться так же?
3. Известно, что вес тела на Луне в 6 раз меньше, чем на Земле. Представьте себе, что вам предложено отправиться на Луну и проверить этот факт экспериментально. Какое оборудование вы возьмете с собой?
4. Уважаемые знатоки! У меня в руках игральная карта: шестерка бубен. Посмотрите внимательно, на карте вы видите изображение ромба. У меня к вам такой вопрос: почему на картах бубновой масти изображен именно ромб, а не что-нибудь другое?
5. Какая борона сидит глубже в земле: массой в 60кг с 20 зубьями или массой 120кг с 60 зубьями?
6. Математик, оказавшись случайно в небольшом городке и желая хоть как-то убить время, решил подстричься. В городке имелось лишь два мастера (у каждого из них своя парикмахерская). Заглянув к одному мастеру, математик увидел, что в салоне грязно, сам мастер одет неряшливо и небрежно подстрижен. В салоне другого мастера было идеально чисто, я владелец был безукоризненно одет и аккуратно подстрижен. Поразмыслив, математик отправился стричься к первому мастеру. Уважаемые знатоки! Не можете ли вы объяснить причину столь странного, на первый взгляд, решения математика?
7. В 1271 г. один венецианский купец отправился в путешествие по странам Востока. Поход оказался длительным и чрезвычайно интересным. Он побывал в Армении, в Персии, в Индии... 17 лет он прожил в Китае. В 1295 г. отважный венецианец вернулся на родину. Через несколько лет он написал книгу о своем путешествии. В книге рассказывается много диковинного. Нос особым восторгом автор описывает богатство китайских вельмож. Купцы Венеции — состоятельные люди. Арифметику знают прекрасно. Свои доходы они считают на тысячи. «Милле», — сочно произносят они. Это и означает «тысяча». Но путешественник, о котором я рассказываю, уверяет, что богатейший китайский вельможа намного богаче достойнейшего из венецианских купцов. Как это выразить, как передать одним словом несметные богатства Востока? И он произносит: «Мильоне!» Получилось необычное, но в общем понятное для итальянца слово. «Миллс» — по-итальянски «тысяча». Окончание «-оне» играет у итальянцев ту же роль, что у нас суффикс «-ищ-». «Мильоне», очевидно, «тыся-чише», «великая тысяча», «тысяча тысяч». Так родилось слово «миллион», означающее «тысяча тысяч». В порыве вдохновения венецианский купец сочинил слово, которым ныне пользуется весь мир. Внимание! Вопрос: Кто был этот купец"
8. В начале сороковых годов нашего века автостроители всего мира столкнулись со странным непонятным явлением. Во время скоростного полета на некоторой, так называемой критической скорости возникла стремительно нарастающая вибрация конструкции. Она внезапно охватывала самолет, и иногда достаточно было нескольких секунд, чтобы машина в воздухе развалилась на куски. С земли казалось, что самолеты взрываются. Многие исследования, проведенные в США, Англии. Германии, не принесли успеха. Полностью разобраться в этой запутанной проблеме удалось лишь известному советскому математику. Были найдены простые и эффективные методы предупреждения вибраций. Угроза самолету и экипажу быта полностью ликвидирована. За выдающийся вклад в решение труднейшей проблемы этот математик в 19-12 г. был удостоен Государственной премии СССР. Вопросы к вам, уважаемые знатоки, таковы: Какое название получило в технике описание явления? Какова фамилия советского математика, о котором я рассказала?
9. Как разделить наследство?
Некий римлянин, умирая, составил завещание в пользу своей жены и ребенка, который должен был родиться. Если бы на свет появился мальчик, то он должен был получить две трети наследства, а жена - одну треть. Если же на свет появится девочка, то она должна получить одну треть, а две трети — мать. Но на свет пришли близнецы — мальчик и девочка. Как разделить наследство?
10. Назовите стороны египетского треугольника.
11. Валентин Берестов в книге «Меня приглашают на Марс» описывает следующую ситуацию:
«Берем кошку, подвешиваем ей на хвост жестянку и... сообщаем кошке некоторое ускорение а. Чем быстрее бежит кошка, тем громче звенит жестянка. Чем громче звенит жестянка, тем быстрее бежит кошка».
Внимание! Вопрос: С какой скоростью должна двигаться кошка, чтобы не слышать звон жестянки?
Ответы на вопросы
1. 1050.
2. Первоначальный объем мыла равнялся xyz;.
спустя 7 дней объем мыла составлял 1/2х*1/2у1/2z=1/8xyz. Разность оставляет xyz-1/8xyz=7/8xyz. Столько мыла смылось за 7 дней. Мыла хватит на 1 один день, так как осталось всего 1/8 часть первоначального количества.
3. Нужно взять тело, вес которого известен на земле, пружинные весы (динамометр) чашечные весы не годятся, их показания на Земле и на Луне будут одинаковыми: сами гири «уменьшаются» в весе в 6 раз.
4. Слово «ромб» происходит от греческого слова «ромбос», означающего «бубен». Мы привыкли к тому, что бубен имеет форму круга, но раньше бубны имели форму квадрата или ромба.
5. Первая борона уходит в землю глубже, так как давление на каждый зуб больше.
6. Поскольку в городе лишь два парикмахера, каждый мастер вынужден стричься у другого. Математик выбрал того из мастеров, кто лучше подстриг своего конкурента.
7. Марко Поло.
8. Явление получило название «флаттер». Математик, решивший задачу, — Мстислав Всеволодович Келдыш (1911-1978), академик, трижды Герой Социалистического труда, выдающийся русский ученый, много лет проработавший на посту Президента АН СССР.
9. Римский юрист Сальвий решил эту задачу так: наследство необходимо разделить на 7 частей: 4/7 получил сын, 2/7 жена и 1/7 дочь. При таком
дележе будет соблюдена воля отца, чтобы сын получил долю, вдвое большую, чем мать, а дочь - вдвое меньшую.
10. Египетским называется прямоугольный треугольник со сторонами 3, 4, 5.
11. Кошка должна двигаться со скоростью, большей звука.
5.5. Дидактические игры
Дидактические игры можно использовать как нетрадиционную форму обучения. Основное обучающее воздействие, принадлежит дидактическому материалу, игровым действиям, которые автоматически ведут учебный процесс, направляя активность детей в определенное русло.
Игровая форма занятий создается на уроках при помощи игровых приемов и ситуаций, которые выступают как средство побуждения, стимулирующие учащихся к деятельности.
Реализация игровых приемов и ситуаций при урочной форме занятий проходит по следующим основным направлениям: дидактическая цель ставится перед учащимися в форме игровой задачи; учебная деятельность учащихся подчиняется правилам игры; учебный материал используется в качестве средства игры; в учебную деятельность вводится элемент соревнования, который переводит дидактическую задачу в игровую; успешность выполнения дидактического задания связывается с игровым результатом.
В процессе игры у детей вырабатывается привычка сосредотачиваться, мыслить самостоятельно, развивается внимание, стремление к знаниям. Увлекшись, дети не замечают, что учатся: познают, запоминают новое, ориентируются в необычных ситуациях, пополняют запас представлений, понятий, развивают фантазию. Даже самые пассивные из детей включаются в игру с огромным желанием, прилагая все усилия, чтобы не подвести товарищей по игре.
Во время игры Деи очень внимательны, сосредоточены и дисциплинированны.
В термине «дидактическая игра» подчеркивается ее педагогическая направленность, отображается многообразие применений. Поэтому есть основания утверждать, что использование дидактической игры в системе обучения математике в 5-11 классах является важным средством интенсификации учебной деятельности школьников, осуществление преемственности между обучением в различных классах.
Дальше рассмотрим некоторые пути и формы использования дидактических игр и игровых ситуаций на уроках математики.
Уроки математики с применением дидактических игр.
Рассмотрим на конкретных примерах организационную и содержательную стороны построения уроков математики, содержащих элементы игры как форму взаимодействия учителя с учащимися, в процессе которой через систему игровых действий реализуются учебно-воспитательные возможности, заложенные в содержании учебного материала.
Алгебра, IX класс.
Тема: «Определение арифметической и геометрической прогрессий».
Цель урока: усвоение учащимися понятий арифметической и геометрической прогрессий.
Оборудование: кодоскоп, диапозитивы, содержащие дидактический материал (количество заданий четное, поровну для I и II команд), указка.
На доске написано:
I команда II команда
Ниже ведется запись полученных очков.
Правила игры.
1) Класс разбивается на две команды:
I команда — ученики первого ряда и половины второго ряда;
II команда — ученики третьего ряда и половины второго ряда.
2) Выбираются капитаны команд.
3) Капитаны команд назначают консультантов. Они должны помогать школьникам из другой команды отвечать на вопросы, предложенные учителем в ходе урока. Их работа приносит дополнительные очки своей команде. Плохо проведенная консультация или отказ от проведения консультации наказывается очками в пользу команды противника.
4) После слов «Консультация окончена» школьники занимают свои места. В противном случае команда наказывается штрафными очками.
5) Для участия во всех видах работы ученики вызываются к доске капитанами команд.
Ход урока
I этап — консультация. Актуализируются знания учащихся по таким вопросам: определение последовательности, возрастающие и убывающие последовательности, способы задания числовых последовательностей, рекуррентный способ задания последовательности, построение графика последовательности, среднее арифметическое и среднее геометрическое двух чисел.
На консультацию отводится 10—12 минут. Консультируют учеников представители других команд. Разрешаются и взаимоконсультации.

Рис. 57 Рис. 58
При необходимости консультирует учитель. За консультации команды получают очки.
II этап — учебно-познавательная работа учащихся по самостоятельному приобретению новых знаний.
Предлагается разделить страницу тетради на две части и слева написать «Арифметическая прогрессия», а справа — «Геометрическая прогрессия». На доску (слева) проецируется задача, приводящая к арифметической, а справа — к геометрической прогрессии. К ним проецируются вопросы и задания, которые необходимо выполнить.
Задача 1. Вертикальные стержни фермы имеют такую длину: наименьший а=5дм, а каждый следующий на 2дм длиннее. Записать длину семи стержней. (рис.57)
Задача 2. В благоприятных условиях бактерии размножаются так, что на протяжении одной минуты одна из них делится на две. Записать колонию, рожденную одной бактерией за 7 мин (рис. 58).
1) Записать последовательность в соответствии с условием задачи.
2) Записать эту же последовательность с помощью таблицы.
3) Найти разность d между предыдущим и последующим членами последовательности в первой задаче и частное q от деления последующего члена на предыдущий во второй задаче.
4) Задать эти последовательности рекуррентным способом.
5) Дать определение арифметической (геометрической) прогрессии.
6) Найти среднее арифметическое (геометрическое) чисел 2 и 8. Записать найденное число с данными в порядке возрастания. Образуют ли эти числа арифметическую (геометрическую) прогрессию?
7) Справедлива ли такая зависимость для трех последовательных членов рассматриваемых последовательностей?
8) Доказать, что для членов арифметической прогрессии справедлива закономерность аn+1=(an+an+2)/2, а для членов геометрической прогрессии — закономерность bn+1=√bn*bn+2
Сначала школьники проделывают всю работу на доске и в тетрадях для арифметической прогрессии, а потом — для геометрической или для обеих сразу.
Записи ответов учащихся, которые поочередно вызываются к доске от каждой команды:

В процессе игры учащиеся следят за ответами товарищей, записывают все в тетради и готовятся ответить на предложенный вопрос. Учитель предлагает вопрос, а капитаны команд называют для ответов учащихся из других команд. Подводятся итоги первых двух этапов игры.
III этап — работа школьников по решению упражнений и самостоятельному составлению задач, приводящих к записи арифметической и геометрической прогрессией. За образец взять задачи № 380, 401*.
Решить упражнения:
I команда II команда
№ 433 (а), № 433 (б),
446 (а) 446 (б)
IV этап — подведение итогов работы. Выигравшая команда объявляется победительницей, а многие учащиеся получают оценку. Задание на дом.
Игра: математический поединок. 7 класс «формулы сокращенного умножения»
В конце учебного года трудно удержать внимание учеников на решении задач. Однако курс повторять надо — впереди итоговая контрольная работа. А каждому учителю хочется, чтобы его дети с испытанием справились хорошо. Вот и приходится придумывать такие формы работы, которые смогут «оторвать» учеников от весны, заинтересовать их уроком.
Игру «Математический поединок» по одной из основных тем курса алгебры VII класса — «Формулы сокращенного умножения». Ее можно проводить не только при итоговом повторении, но и сразу после изучения этой темы.
Весь класс разбивается на 4 команды. Команды выбирают капитанов, которые получают у учителя карточки: на одной стороне листа записано задание, а на другой - необходимо записать фамилии игроков команды.
Каждая команда может выбирать спою тактику игры: либо учащиеся сообща решают все предложенные задания, либо каждый игрок выбирает одно задание, выполнив которое рассказывает свое решение и ставит на обсуждение его рациональность.
Все члены команды, кроме капитана (он работаете карточкой), записывают решение каждого примера в своей тетради.
Правила игры
1) Каждый правильно решенный пример оценивается пятью баллами.
2) За верное, но нерациональное решение примера, выставляется три балла.
3) В случае отсутствия решения одного примера в тетради игрока снимается один балл.
4) У команды, нарушившей дисциплину, снимается один балл.
5) Команде, первой сдавшей карточку с решениями всех примеров, добавляется три балла.
6) Команда может попросить консультацию учителя (не более одной), но за это снимается один балл.
Команда, получившая наибольшее число баллов, занимает первое место, и всем ее участникам выставляются в журнал пятерки.
Карточки-задания
1 команда
1. Найти значение выражения 100b2-60b + 9 при b = 2.
2. Доказать, что 252 — 122 делится на 13.
3. Представить в виде многочлена выражение (0.3с + 0,2d)*(0,2d - 0,3с).
4. Используя формулу квадрата суммы или разности, вычислить 482.
5. Вычислить, используя формулу разности квадратов, 59*61.
6. Разложить на простые множители 74- 1.
2 команда
1. Найти значение выражения 4x2+12x+9 при x = 5.
2. Что больше: 262-242 или 272-252?
3. Представить в виде многочлена выражение (11c2+a3)*(-a3+11c2).
4. Используя формулу квадрата суммы или разности, вычислить 612.
5. Вычислить, используя формулу разности квадратов, 199*201.
6. Решить уравнение y2+4y+3=0.
3 команда
1. Найти значение выражения 25y2 -70y + 49 при у = 3.
2. Доказать, что 372 — 142 делится на 23.
3. Представить в виде многочлена выражение (0,8x + y4)*(0,8x – у4).
4. Используя формулу квадрата суммы или разности, вычислить 522.
5. Вычислить, используя формулу разности квадратов, 102 * 98.
6. Разложить на простые множители 64 - 1.
4 команда
1. Найти значение выражения 49m2 – 28m + 4 при m = 2.
2. Что больше: 452 — 312 или 442 — 302 ?
3. Представить в виде многочлена выражение (9m - 6х2)*(6x2 + 9m).
4. Используя формулу квадрата суммы или разности, вычислить 462.
Похожие работы
... умственными способностями; план Трампа - вариативное, свободное, открытое учение и т.д.), многие учителя, творчески подходящие к своей профессиональной деятельности, считают главными при выборе форм организации обучения такие основания: 1) выявление детей, отличающихся характером восприятия учебной информации, типом общения со сверстниками, учителями и др.; 2)определение тех качеств, которые ...
... –ученик, многообразием видов деятельности субъектов (игровая, дискуссионно-оценочная, рефлексивная), базирующихся на активных методах обучения (проблемном, исследовательском, “методе прямого доступа”)”. [29] Глава 2. Урок как основная форма организации обучения технологии 2.1 Разработка учебно-методического комплекса организации и проведения уроков технологии Техническое творчество ...
... нецелесообразно, так как нетрадиционное может быстро стать традиционным, что в конечном счете приведет к падению у учащихся интереса к предмету. Развивающий и воспитывающий потенциал нетрадиционных форм урока можно охарактеризовать с помощью определения следующих целей обучения: - формирование у учащихся интереса и уважения к культуре страны изучаемого языка; - воспитание культуры ...
... праздника, приподнятое настроение, позволяют ребятам проявить свою инициативу, способствуют выработке у них чувства взаимопомощи, коммуникативных умений. Как правило, театрализованные уроки разделяют по форме их организации: спектакль, салон, сказка, студия и т.д. При подготовке таких уроков даже работа над сценарием и изготовление элементов костюмов становятся результатом коллективной ...
0 комментариев