Навигация
Математическое ожидание и дисперсия являются примерами моментов случайной величины, которые определяются следующим образом
41.1. Математическое ожидание и дисперсия являются примерами моментов случайной величины, которые определяются следующим образом.
Начальным моментом порядка ![]() непрерывной случайной величины с плотностью распределения вероятности
непрерывной случайной величины с плотностью распределения вероятности ![]() называется число
называется число
 . (41.1)
. (41.1)
Порядок момента ![]() - это неотрицательное целое число, т.е.
- это неотрицательное целое число, т.е. ![]() .
.
Начальным моментом порядка ![]() дискретной случайной величины
дискретной случайной величины ![]() , принимающей значения
, принимающей значения ![]() с вероятностями
с вероятностями ![]() ,
, ![]() , называется число
, называется число
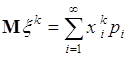 . (41.2)
. (41.2)
Определение (41.1) можно рассматривать как универсальное определение для непрерывных и для дискретных случайных величин. В последнем случае плотность вероятности выражается через ![]() - функцию согласно формуле (34.4). Однако на практике для вычисления момента дискретной величины удобнее использовать соотношение (41.2).
- функцию согласно формуле (34.4). Однако на практике для вычисления момента дискретной величины удобнее использовать соотношение (41.2).
Центральным моментом порядка ![]() случайной величины
случайной величины ![]() называется число
называется число
![]() . (41.3)
. (41.3)
Для непрерывной случайной величины ![]() с плотностью вероятности
с плотностью вероятности ![]() центральный момент порядка
центральный момент порядка ![]() имеет вид:
имеет вид:
 . (41.4)
. (41.4)
41.2. Из всего множества начальных и центральных моментов обычно используются моменты невысоких порядков, до ![]() включительно, как более простые характеристики случайной величины. Применение моментов высоких порядков,
включительно, как более простые характеристики случайной величины. Применение моментов высоких порядков, ![]() , ограничено. Во-первых, при больших
, ограничено. Во-первых, при больших ![]() моменты могут не существовать, поскольку могут расходиться интегралы (41.1), (41.4). И во-вторых, интерпретация моментов высших порядков затруднена.
моменты могут не существовать, поскольку могут расходиться интегралы (41.1), (41.4). И во-вторых, интерпретация моментов высших порядков затруднена.
Рассмотрим начальные моменты, начиная с ![]() . При этом из (41.1) следует
. При этом из (41.1) следует
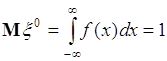 . (41.5)
. (41.5)
Итак, начальный момент нулевого порядка ![]() для любой случайной величины, следовательно, этот момент не отражает каких-либо свойств случайной величины, т.е. не является ее характеристикой. При
для любой случайной величины, следовательно, этот момент не отражает каких-либо свойств случайной величины, т.е. не является ее характеристикой. При ![]() из (41.1) следует, что момент первого порядка - это математическое ожидание случайной величины. Разные случайные величины могут иметь разные математические ожидания, и поэтому число
из (41.1) следует, что момент первого порядка - это математическое ожидание случайной величины. Разные случайные величины могут иметь разные математические ожидания, и поэтому число ![]() является характеристикой случайной величины: число
является характеристикой случайной величины: число ![]() указывает положение центра ее плотности вероятности.
указывает положение центра ее плотности вероятности.
Момент второго порядка
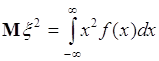 (41.6)
(41.6)
- это среднее квадрата ![]() случайной величины, и т.д.
случайной величины, и т.д.
Рассмотрим аналогично центральные моменты (41.4). При ![]() получаем
получаем ![]() - одинаковый результат для любой случайной величины. Поэтому данный момент не является характеристикой случайной величины, поскольку не отражает каких-либо ее свойств. При
- одинаковый результат для любой случайной величины. Поэтому данный момент не является характеристикой случайной величины, поскольку не отражает каких-либо ее свойств. При ![]()
![]() . Этот результат также одинаков для любой случайной величины, поэтому центральный момент первого порядка не является характеристикой случайной величины. При
. Этот результат также одинаков для любой случайной величины, поэтому центральный момент первого порядка не является характеристикой случайной величины. При ![]() из (41.4) получаем дисперсию
из (41.4) получаем дисперсию
![]()
 (41.7)
(41.7)
- важнейшую числовую характеристику случайной величины и т.д.
Моменты третьего и четвертого порядков будут рассмотрены в дальнейшем.
Неравенство Чебышева42.1. Пусть случайная величина ![]() имеет конечный момент второго порядка
имеет конечный момент второго порядка ![]() , тогда
, тогда
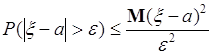 , (42.1)
, (42.1)
где ![]() - любое действительное число и
- любое действительное число и ![]() . Соотношение (42.1) называют неравенством Чебышева.
. Соотношение (42.1) называют неравенством Чебышева.
Сначала рассмотрим доказательство неравенства, следующего из (42.1) при ![]() :
:
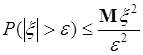 . (42.2)
. (42.2)
Доказательство неравенства Чебышева удобнее рассматривать отдельно для непрерывной и для дискретной случайных величин. При этом доказательства являются относительно простыми, а ход доказательств вполне очевиден. В то время как универсальное доказательство, справедливое и для непрерывной и для дискретной случайных величин оказывается значительно более сложным. Рассмотрим непрерывную случайную величину ![]() с плотностью вероятности
с плотностью вероятности ![]() . Тогда в соотношении
. Тогда в соотношении ![]()
![]() первое слагаемое можно представить в виде
первое слагаемое можно представить в виде
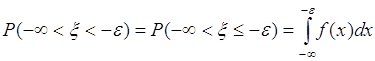 ,
,
поэтому
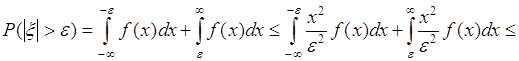
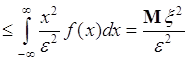 .
.
Здесь использовано неравенство ![]() - справедливое на области интегрирования. Полученное выражение совпадает с неравенством (42.2). Аналогично выполняется доказательство для дискретной случайной величины.
- справедливое на области интегрирования. Полученное выражение совпадает с неравенством (42.2). Аналогично выполняется доказательство для дискретной случайной величины.
Теперь случайную величину ![]() в (42.2) можно заменить на случайную величину
в (42.2) можно заменить на случайную величину ![]() , где
, где ![]() - любое действительное число, тогда из (42.2) следует неравенство Чебышева (42.1). Это неравенство определяет границу сверху для вероятности
- любое действительное число, тогда из (42.2) следует неравенство Чебышева (42.1). Это неравенство определяет границу сверху для вероятности ![]() или, как говорят, больших уклонений
или, как говорят, больших уклонений ![]() случайной величины
случайной величины ![]() от числа
от числа ![]() . Большие уклонения понимаются в смысле их превышения над заданным числом
. Большие уклонения понимаются в смысле их превышения над заданным числом ![]() .
.
42.2. Пусть ![]() , тогда неравенство Чебышева (42.1) имеет вид
, тогда неравенство Чебышева (42.1) имеет вид
 . (42.3)
. (42.3)
Теперь минимальное уклонение ![]() можно измерять в единицах среднеквадратического уклонения
можно измерять в единицах среднеквадратического уклонения ![]() случайной величины
случайной величины ![]() , т.е. положить
, т.е. положить
![]() , (42.4)
, (42.4)
где ![]() - коэффициент пропорциональности. Подставим (42.4) в (42.3), тогда
- коэффициент пропорциональности. Подставим (42.4) в (42.3), тогда
 . (42.5)
. (42.5)
Если правая часть ![]() , то (42.5) не представляет какого-либо ограничения на случайную величину, поскольку вероятность
, то (42.5) не представляет какого-либо ограничения на случайную величину, поскольку вероятность ![]() не может выходить за пределы интервала
не может выходить за пределы интервала ![]() . Поэтому коэффициент
. Поэтому коэффициент ![]() в (42.5) имеет смысл рассматривать только большим:
в (42.5) имеет смысл рассматривать только большим: ![]() . Отсюда очевидна интерпретация неравенства Чебышева как неравенства, определяющего границу сверху вероятности больших уклонений.
. Отсюда очевидна интерпретация неравенства Чебышева как неравенства, определяющего границу сверху вероятности больших уклонений.
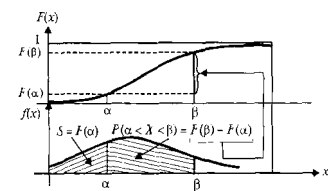
Пусть ![]() - непрерывная случайная величина с плотностью вероятности
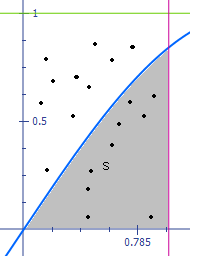
- непрерывная случайная величина с плотностью вероятности ![]() , тогда неравенству Чебышева (42.1) можно дать простую геометрическую интерпретацию, представленную на рис. 42.1.
, тогда неравенству Чебышева (42.1) можно дать простую геометрическую интерпретацию, представленную на рис. 42.1.

Рис. 42.1. Иллюстрация к неравенству Чебышева.
Здесь указаны числа ![]() ,
, ![]() и
и ![]() , заштрихованная площадь - это вероятность
, заштрихованная площадь - это вероятность
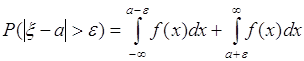 .
.
Среднее и дисперсия случайной величины ![]() - это числа, которые определяют такие свойства ее плотности вероятности
- это числа, которые определяют такие свойства ее плотности вероятности ![]() как положение центра и эффективную ширину. Очевидно, эти два числа не отражают всех особенностей плотности, в частности, степень симметрии или асимметрии плотности относительно математического ожидания - это новая характеристика, которую можно определить как некоторое число.
как положение центра и эффективную ширину. Очевидно, эти два числа не отражают всех особенностей плотности, в частности, степень симметрии или асимметрии плотности относительно математического ожидания - это новая характеристика, которую можно определить как некоторое число.
Для любой симметричной плотности ![]() центральные моменты нечетного порядка равны нулю (доказательство приводится ниже). Поэтому простейший среди них - центральный момент третьего порядка может характеризовать асимметрию плотности распределения:
центральные моменты нечетного порядка равны нулю (доказательство приводится ниже). Поэтому простейший среди них - центральный момент третьего порядка может характеризовать асимметрию плотности распределения:
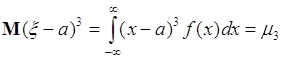 , (43.1)
, (43.1)
где ![]() - математическое ожидание,
- математическое ожидание, ![]() - центральный момент
- центральный момент ![]() - го порядка.
- го порядка.
Асимметрию принято характеризовать коэффициентом асимметрии
 , (43.2)
, (43.2)
где ![]() - дисперсия случайной величины
- дисперсия случайной величины ![]() .
.
Рассмотрим доказательство утверждения о том, что для симметричной плотности ![]() центральные моменты нечетных порядков равны нулю.
центральные моменты нечетных порядков равны нулю.
1). Пусть ![]() - симметричная функция относительно некоторой точки
- симметричная функция относительно некоторой точки ![]() , тогда
, тогда
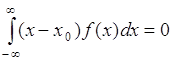 , (43.3)
, (43.3)
поскольку ![]() - антисимметричная функция относительно
- антисимметричная функция относительно ![]() . Отсюда следует:
. Отсюда следует:
 . (43.4)
. (43.4)
Таким образом, если ![]() - симметричная функция относительно точки
- симметричная функция относительно точки ![]() , то
, то ![]() - точка симметрии плотности вероятности – это математическое ожидание случайной величины.
- точка симметрии плотности вероятности – это математическое ожидание случайной величины.
2). Пусть ![]() - нечетное целое и
- нечетное целое и ![]() - симметричная функция, тогда
- симметричная функция, тогда 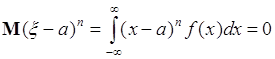 ,
поскольку
,
поскольку ![]() - симметрична относительно математического ожидания
- симметрична относительно математического ожидания ![]() , и
, и ![]() - антисимметрична относительно
- антисимметрична относительно ![]() .
.
Выражение (43.2) для ![]() можно представить через начальные моменты
можно представить через начальные моменты ![]() ,
, ![]() . Из определения следует:
. Из определения следует:
![]() .
.
Аналогично центральный момент третьего порядка
![]()
![]() .
.
Пусть случайная величина ![]() имеет плотность вероятности:
имеет плотность вероятности:
 , (43.6)
, (43.6)
(распределение Рэлея), тогда вычисление ![]() и подстановка в (43.2) приводит к результату
и подстановка в (43.2) приводит к результату ![]() .
.
Плотность вероятности с ![]() имеет более тяжелый «хвост» в области больших положительных аргументов, и наоборот, при
имеет более тяжелый «хвост» в области больших положительных аргументов, и наоборот, при ![]() более тяжелым является «хвост» плотности в области отрицательных аргументов.
более тяжелым является «хвост» плотности в области отрицательных аргументов.
Характеристикой степени сглаженности вершины плотности вероятности является число
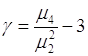 , (43.1)
, (43.1)
называемое коэффициентом эксцесса.
Определим ![]() для нормального распределения. Поскольку
для нормального распределения. Поскольку ![]() , то осталось вычислить
, то осталось вычислить
 .
.
Пусть ![]() , тогда
, тогда
 .
.
Вычислим интеграл способом «по частям»:
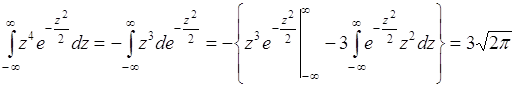 .
.
Таким образом, ![]() . Подставим полученные результаты в (43.6), тогда
. Подставим полученные результаты в (43.6), тогда ![]() .
.
Если ![]() , то плотность вероятности имеет более высокую и более острую вершину, чем кривая плотности нормального распределения с той же дисперсией. Если
, то плотность вероятности имеет более высокую и более острую вершину, чем кривая плотности нормального распределения с той же дисперсией. Если ![]() , то вершина плотности распределения более плоская, чем у нормального распределения.
, то вершина плотности распределения более плоская, чем у нормального распределения.
Среднеквадратическая ошибка
Пусть ![]() - неизвестный параметр (число), характеризующий состояние системы. Для определения параметра
- неизвестный параметр (число), характеризующий состояние системы. Для определения параметра ![]() проводится опыт (измерение). Ситуация осложняется тем, что в процессе измерения на величину
проводится опыт (измерение). Ситуация осложняется тем, что в процессе измерения на величину ![]() накладывается помеха. Таким образом, измерению подлежит не число
накладывается помеха. Таким образом, измерению подлежит не число ![]() , а некоторая случайная величина
, а некоторая случайная величина ![]() , значения которой в каждом опыте точно предсказать невозможно.
, значения которой в каждом опыте точно предсказать невозможно.
Случайную величину ![]() будем называть оценкой параметра
будем называть оценкой параметра ![]() . Тогда
. Тогда ![]() - ошибка, также случайная величина. Характеристикой качества оценки
- ошибка, также случайная величина. Характеристикой качества оценки ![]() является ее среднеквадратическая ошибка
является ее среднеквадратическая ошибка
![]() . (45.1)
. (45.1)
Преобразуем это выражение:
 (45.2)
(45.2)
Величина ![]() - детерминированная, поэтому ее можно вынести за оператор
- детерминированная, поэтому ее можно вынести за оператор ![]() , следовательно, второе слагаемое
, следовательно, второе слагаемое
![]()
Первое слагаемое (45.2) по определению
![]()
- дисперсия случайной величины ![]() . Введем обозначение
. Введем обозначение
![]() . (45.3)
. (45.3)
Число ![]() называется смещением оценки
называется смещением оценки ![]() . Таким образом, из (45.2) следует
. Таким образом, из (45.2) следует
![]() (45.4)
(45.4)
- среднеквадратическая ошибка является суммой двух неотрицательных слагаемых. Первое из них – дисперсия, или случайная (стохастическая) компонента ошибки, а второе – квадрат смещения – систематическая ошибка. Если ![]() , то оценка
, то оценка ![]() называется несмещенной.
называется несмещенной.
Пусть случайная величина ![]() - имеет плотность вероятности
- имеет плотность вероятности ![]() . Тогда процедуре измерения можно дать геометрическую интерпретацию. На рис. 45.1 представлен график плотности вероятности оценки и показана систематическая ошибка
. Тогда процедуре измерения можно дать геометрическую интерпретацию. На рис. 45.1 представлен график плотности вероятности оценки и показана систематическая ошибка ![]() , и случайная ошибка
, и случайная ошибка ![]() .
.
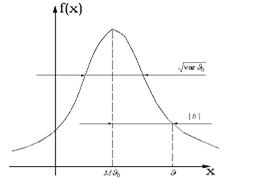
Рис. 45.1. Плотность вероятности оценки,
случайная и систематическая части ошибки.
Очевидно, идеальная процедура измерения (с нулевой среднеквадратической ошибкой) – это процедура, для которой плотность ![]() близка к функции
близка к функции ![]() . Тогда
. Тогда ![]() , точка
, точка ![]() , а эффективная ширина
, а эффективная ширина ![]() .
.
Характеристической функцией случайной величины ![]() называется функция
называется функция
![]() ,
, ![]() . (46.1)
. (46.1)
Пусть ![]() - непрерывная случайная величина с плотностью вероятности
- непрерывная случайная величина с плотностью вероятности ![]() , тогда ее характеристическая функция
, тогда ее характеристическая функция
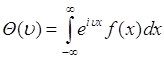 (46.2)
(46.2)
- является интегральным преобразованием, которое называется преобразованием Фурье от плотности вероятности ![]() . Известно, что преобразование Фурье является взаимно однозначным. Поэтому существует обратное преобразование, которое определяет плотность вероятности
. Известно, что преобразование Фурье является взаимно однозначным. Поэтому существует обратное преобразование, которое определяет плотность вероятности ![]() через характеристическую функцию
через характеристическую функцию ![]() . Это преобразование имеет вид
. Это преобразование имеет вид
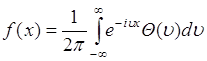 . (46.3)
. (46.3)
Соотношения (46.2) и (46.3) образуют пару преобразований Фурье.
Для дискретной случайной величины ![]() , принимающей значения
, принимающей значения ![]() с вероятностями
с вероятностями ![]() характеристическая функция, как следует из (46.1), имеет вид
характеристическая функция, как следует из (46.1), имеет вид
 . (46.4)
. (46.4)
Характеристическая функция является полной вероятностной характеристикой случайной величины, также как и функция распределения ![]() или плотность вероятности
или плотность вероятности ![]() . Смысл введения характеристической функции в теории вероятности состоит в том, что имеется класс задач, которые относительно просто решаются с применением преобразования Фурье от плотности вероятности. Роль этого преобразования оказалась столь велика, что в теории появился специальный термин «характеристическая функция» для обозначения этого преобразования.
. Смысл введения характеристической функции в теории вероятности состоит в том, что имеется класс задач, которые относительно просто решаются с применением преобразования Фурье от плотности вероятности. Роль этого преобразования оказалась столь велика, что в теории появился специальный термин «характеристическая функция» для обозначения этого преобразования.
Рассмотрим свойства функции ![]() для непрерывной случайной величины. Для дискретной величины эти свойства доказываются аналогично.
для непрерывной случайной величины. Для дискретной величины эти свойства доказываются аналогично.
1). В общем случае характеристическая функция (46.2) является комплексной. Ее вещественная часть
 (47.1)
(47.1)
- является ![]() - преобразованием от плотности вероятности, и мнимая часть
- преобразованием от плотности вероятности, и мнимая часть
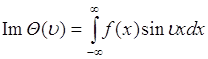 (47.2)
(47.2)
- является ![]() - преобразованием от
- преобразованием от ![]() . Если
. Если ![]() - четная функция, то
- четная функция, то ![]() , тогда характеристическая функция
, тогда характеристическая функция ![]() и является вещественной и четной функцией.
и является вещественной и четной функцией.
2). ![]() . Это свойство следует из (46.2) и условия нормировки для плотности:
. Это свойство следует из (46.2) и условия нормировки для плотности:
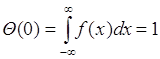 . (47.3)
. (47.3)
3). ![]() - функция
- функция ![]() имеет глобальный максимум в точке
имеет глобальный максимум в точке ![]() . Доказательство следует из (46.2):
. Доказательство следует из (46.2):
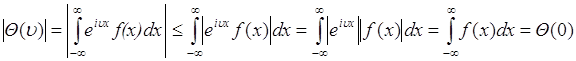 .
.
4). ![]()
5). Характеристическая функция непрерывна. Для доказательства рассмотрим приращение ![]() аргумента функции
аргумента функции ![]() , такое, что
, такое, что ![]() , где
, где ![]() - положительное число. Тогда имеет место следующая цепочка преобразований:
- положительное число. Тогда имеет место следующая цепочка преобразований:

 . (47.4)
. (47.4)
Пусть ![]() и число
и число
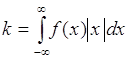 , (47.5)
, (47.5)
тогда из (47.4) следует
![]() . (47.6)
. (47.6)
Таким образом, выполняется определение непрерывности функции ![]() : для любого
: для любого ![]() можно выбрать положительное
можно выбрать положительное ![]() , что из условия
, что из условия ![]() следует
следует ![]() .
.
48.1. Пусть ![]() - случайная величина с характеристической функцией
- случайная величина с характеристической функцией ![]() . Найти характеристическую функцию
. Найти характеристическую функцию ![]() случайной величины
случайной величины
![]() , (48.1)
, (48.1)
где ![]() - числа. По определению
- числа. По определению
![]() . (48.2)
. (48.2)
48.2. Найти характеристическую функцию ![]() гауссовой случайной величины
гауссовой случайной величины ![]() . По формуле (46.2)
. По формуле (46.2)
 . (48.3)
. (48.3)
Выполним замену переменной интегрирования ![]() на переменную
на переменную ![]() , тогда
, тогда ![]() и
и
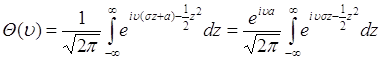 . (48.4)
. (48.4)
Показатель в подынтегральном выражении преобразуем следующим образом:
![]() .
.
Подстановка этого результата в (48.4) приводит к выражению
![]() . (48.5)
. (48.5)
Отсюда следует, что характеристическая функция гауссовой случайной величины ![]() при
при ![]() является вещественной и четной функцией.
является вещественной и четной функцией.
49.1. Вычислим производную порядка ![]() характеристической функции (46.1) при
характеристической функции (46.1) при ![]() :
:
 , (49.1)
, (49.1)
где ![]() - начальный момент
- начальный момент ![]() порядка случайной величины
порядка случайной величины ![]() . Пусть существуют все моменты
. Пусть существуют все моменты ![]() ,
, ![]() , тогда существуют производные (49.1) характеристической функции при
, тогда существуют производные (49.1) характеристической функции при ![]() . Поэтому функцию
. Поэтому функцию ![]() можно разложить в ряд Тейлора около точки
можно разложить в ряд Тейлора около точки ![]() :
:
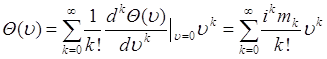 . (49.2)
. (49.2)
Отметим, что здесь первое слагаемое ![]() . Выражение (49.2) называют иногда разложением характеристической функции по моментам, имея ввиду тот факт, что коэффициенты при
. Выражение (49.2) называют иногда разложением характеристической функции по моментам, имея ввиду тот факт, что коэффициенты при ![]() определяются начальными моментами
определяются начальными моментами ![]() .
.
Для непрерывной случайной величины с плотностью вероятности ![]() соотношение (49.1) можно представить в виде:
соотношение (49.1) можно представить в виде:
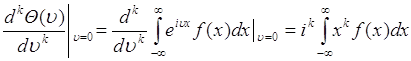 . (49.3)
. (49.3)
Таким образом, существование производной порядка ![]() характеристической функции при
характеристической функции при ![]() (или начального момента
(или начального момента ![]() ) определяется поведением плотности вероятности
) определяется поведением плотности вероятности ![]() при
при ![]() , от которого зависит существование интеграла (49.3).
, от которого зависит существование интеграла (49.3).
49.2. Функция
![]() (49.4)
(49.4)
называется кумулянтной функцией случайной величины ![]() . Кумулянтная функция является полной вероятностной характеристикой случайной величины, также, как и
. Кумулянтная функция является полной вероятностной характеристикой случайной величины, также, как и ![]() . Смысл введения кумулянтной фукнции заключается в том, что эта функция зачастую оказывается наиболее простой среди полных вероятностных характеристик, т.е. среди
. Смысл введения кумулянтной фукнции заключается в том, что эта функция зачастую оказывается наиболее простой среди полных вероятностных характеристик, т.е. среди ![]() . Например, для гауссовой случайной величины из (48.5) следует
. Например, для гауссовой случайной величины из (48.5) следует
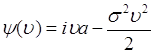 . (49.5)
. (49.5)
Кумулянтную функцию можно представить рядом, аналогично соотношению (49.2) для характеристической функции:
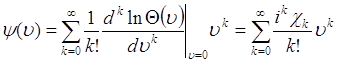 , (49.6)
, (49.6)
где число
 (49.7)
(49.7)
называется кумулянтом ![]() порядка случайной величины
порядка случайной величины ![]() . Из (49.7) следует
. Из (49.7) следует ![]() , поэтому суммирование в (49.6) можно начинать с
, поэтому суммирование в (49.6) можно начинать с ![]() , а поскольку
, а поскольку ![]() для любой случайной величины, то
для любой случайной величины, то ![]() не является характеристикой случайной величины.
не является характеристикой случайной величины.
Вычислим кумулянты для гауссовой случайной величины. Из (49.7), (49.5)
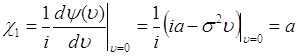 , (49.8)
, (49.8)
 . (49.9)
. (49.9)
Для ![]() производная
производная ![]() , следовательно, гауссова случайная величина имеет только два кумулянта
, следовательно, гауссова случайная величина имеет только два кумулянта ![]() и
и ![]() отличных от нуля, остальные кумулянты - нулевые. Поэтому ряд (49.6) для гауссовой величины состоит из двух слагаемых.
отличных от нуля, остальные кумулянты - нулевые. Поэтому ряд (49.6) для гауссовой величины состоит из двух слагаемых.
Похожие работы
... . Г. Моделирование случайной величины с нормальным распределением. Случайная величина имеет нормальный закон распределения, если ее функция распределения имеет вид: , где и — параметры. Для компьютерного моделирования случайной величины с нормальным законом распределения можно использовать как метод обратных функций, так и метод, специально разработанный для нормального закона. Согласно ...
... , очень мала и равна 0,0027. Такие события считаются практически невозможными. В этом и состоит правило «трех сигм»: если случайная величина распределена по нормальному закону, то ее отклонение от математического ожидания практически не превышает±3σ. Понятие о теоремах, относящихся к группе «центральной предельной теоремы» В теоремах этой группы выясняются условия, при которых возникает ...
... критических точек распределения ([1], стр. 465), по уровню значимости =0,05 и числу степеней свободы 8-3=5 находим Т.к. , экспериментальные данные не противоречат гипотезе и о нормальном распределении случайной величины . Для случайной величины : Используя предполагаемый закон распределения, вычислим теоретические частоты по формуле , где - объем выборки, - шаг (разность между ...
... Впрочем, для наиболее распространённых псевдослучайных чисел период столь велик, что превосходит любые практические потребности. Подавляющее большинство расчётов по методу Монте-Карло осуществляется с использованием псевдослучайных чисел. Значения любой случайной величины можно получить путём преобразования значений одной какой-либо случайной величины. Обычно роль такой случайной величины играет ...


0 комментариев