Навигация
Релеевское распределение вероятностей случайной величины определяется плотностью вида
35.5. Релеевское распределение вероятностей случайной величины определяется плотностью вида
 (35.10)
(35.10)
Этой плотности соответствует функция распределения вероятностей ![]() при
при ![]() и равная
и равная
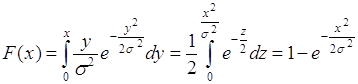 (35.11)
(35.11)
при ![]() .
.
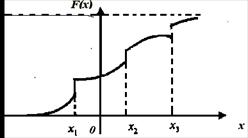
35.6. Рассмотрим примеры построения функции распределения и плотности дискретной случайной величины. Пусть случайная величина ![]() - это число успехов в последовательности из
- это число успехов в последовательности из ![]() независимых испытаний. Тогда случайная величина
независимых испытаний. Тогда случайная величина ![]() принимает значения
принимает значения ![]() ,
, ![]() с вероятностью
с вероятностью ![]() , которая определяется формулой Бернулли:
, которая определяется формулой Бернулли:
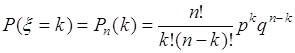 , (35.12)
, (35.12)
где ![]() ,
, ![]() - вероятности успеха и неуспеха в одном опыте. Таким образом, функция распределения вероятностей случайной величины
- вероятности успеха и неуспеха в одном опыте. Таким образом, функция распределения вероятностей случайной величины ![]() имеет вид
имеет вид
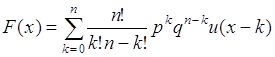 , (35.13)
, (35.13)
где ![]() - функция единичного скачка. Отсюда плотность распределения:
- функция единичного скачка. Отсюда плотность распределения:
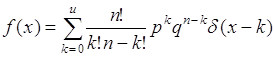 , (35.14)
, (35.14)
где ![]() - дельта-функция.
- дельта-функция.
Кроме дискретных и непрерывных случайных величин существуют еще так называемые сингулярные случайные величины. Эти случайные величины характеризуются тем, что их функция распределения вероятностей ![]() - непрерывна, но точки роста
- непрерывна, но точки роста ![]() образуют множество нулевой меры. Точкой роста
образуют множество нулевой меры. Точкой роста ![]() функции
функции ![]() называется значение ее аргумента
называется значение ее аргумента ![]() такое, что производная
такое, что производная ![]() .
.
Таким образом, ![]() почти всюду на области определения функции. Функцию
почти всюду на области определения функции. Функцию![]() , удовлетворяющую этому условию, также называют сингулярной. Примером сингулярной функции распределения является кривая Кантора (рис. 36.1), которая строится следующим образом. Полагается
, удовлетворяющую этому условию, также называют сингулярной. Примером сингулярной функции распределения является кривая Кантора (рис. 36.1), которая строится следующим образом. Полагается ![]() при
при ![]() и
и ![]() при
при ![]() . Затем интервал
. Затем интервал ![]() разбивается на три равных части (сегмента) и для внутреннего сегмента
разбивается на три равных части (сегмента) и для внутреннего сегмента ![]() определяется значение
определяется значение ![]() - как полусумма уже определенных значений на ближайших сегментах справа и слева. На данный момент функция
- как полусумма уже определенных значений на ближайших сегментах справа и слева. На данный момент функция ![]() определена для
определена для ![]() , ее значение
, ее значение ![]() , и для
, и для ![]() со значением
со значением ![]() . Полусумма этих значений равна
. Полусумма этих значений равна ![]() и определяет значение
и определяет значение ![]() на
внутреннем сегменте
на
внутреннем сегменте ![]() . Затем рассматриваются
отрезки
. Затем рассматриваются
отрезки
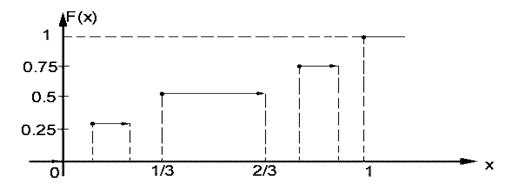
Рис. 36.1. Построение кривой Кантора.
![]() и
и ![]() , каждый из них разбивается на три равных сегмента и функция
, каждый из них разбивается на три равных сегмента и функция ![]() определяется на внутренних сегментах как полусумма ближайших справа и слева заданных значений функции
определяется на внутренних сегментах как полусумма ближайших справа и слева заданных значений функции ![]() . Таким образом, при
. Таким образом, при ![]() функция
функция ![]() - как полусумма чисел
- как полусумма чисел ![]() и
и ![]() . Аналогично на интервале
. Аналогично на интервале ![]() функция
функция ![]() . Затем функция
. Затем функция ![]() определяется на интервале
определяется на интервале ![]() , на котором
, на котором ![]() и т.д.
и т.д.
Суммарная длина всех внутренних сегментов равна

Поэтому, рассматривая интервал ![]() , говорят что функция
, говорят что функция ![]() - постоянная на множестве меры 1, на множестве меры 0 растет, но без скачков.
- постоянная на множестве меры 1, на множестве меры 0 растет, но без скачков.
Известна теорема Лебега. Любая функция распределения ![]() может быть единственным образом представлена в виде суммы трех компонент: дискретной, непрерывной и сингулярной.
может быть единственным образом представлена в виде суммы трех компонент: дискретной, непрерывной и сингулярной.
Сингулярные распределения практически не встречаются в реальных задачах и поэтому исключаются из нашего дальнейшего изучения.
Математическое ожидание случайной величины37.1. Функция распределения вероятностей или плотность вероятности являются полными вероятностными характеристиками случайной величины. Однако, во многих задачах такая полная характеристика случайной величины, с одной стороны, может быть неизвестна для исследователя, а с другой стороны и не обязательна, достаточно ограничиться значением некоторых параметров распределения вероятностей, т.е. некоторых чисел (или числовых характеристик). Здесь уместна аналогия с геометрическим описанием сложной формы твердого тела, когда ограничиваются такими характеристиками (числами) как длина, ширина, высота, объем, момент инерции, и т.д., а детальное описание сложной формы этого тела не рассматривается. Числовыми характеристиками случайных величин чаще всего служат так называемые моменты распределения, простейшим из которых является математическое ожидание случайной величины.
Прежде чем вводить определение математического ожидания случайной величины, рассмотрим выражение среднего арифметического результатов измерения дискретной случайной величины. Пусть случайная величина ![]() может принимать значения
может принимать значения ![]() соответственно с вероятностями
соответственно с вероятностями ![]() . Результат измерения случайной величины
. Результат измерения случайной величины ![]() в каждом опыте - это одно из чисел
в каждом опыте - это одно из чисел ![]() . Пусть выполнено
. Пусть выполнено ![]() опытов, среди них в
опытов, среди них в ![]() опытах случайная величина
опытах случайная величина ![]() принимала значение
принимала значение ![]() , в
, в ![]() опытах - значение
опытах - значение ![]() ,..., в
,..., в ![]() опытах - значение
опытах - значение ![]() . Очевидно,
. Очевидно, ![]() - полное число опытов. Пусть
- полное число опытов. Пусть ![]() - среднее арифметическое результатов измерения случайной величины
- среднее арифметическое результатов измерения случайной величины ![]() в
в ![]() опытах, тогда
опытах, тогда
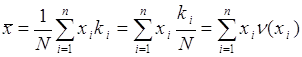 , (37.1)
, (37.1)
где ![]() - частота появления числа
- частота появления числа ![]() при измерении случайной величины
при измерении случайной величины ![]() в
в ![]() опытах. С увеличением числа опытов
опытах. С увеличением числа опытов ![]() величина
величина ![]() приближается к числу
приближается к числу ![]() . Поэтому для того, чтобы определить теоретический аналог среднего арифметического
. Поэтому для того, чтобы определить теоретический аналог среднего арифметического ![]() достаточно в формуле (37.1) частоту
достаточно в формуле (37.1) частоту ![]() заменить на вероятность
заменить на вероятность ![]() . Это приводит к следующему определению.
. Это приводит к следующему определению.
Математическим ожиданием (средним, статистическим средним) дискретной случайной величины ![]() , принимающей значения
, принимающей значения ![]() с вероятностями
с вероятностями ![]() , называется число
, называется число
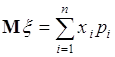 . (37.2)
. (37.2)
Если множество значений дискретной случайной величины счетно: ![]() , то в (37.2) полагается
, то в (37.2) полагается ![]() .
.
Пусть ![]() - однозначная функция одной переменной,
- однозначная функция одной переменной, ![]() - дискретная случайная величина, принимающая значения
- дискретная случайная величина, принимающая значения ![]() с вероятностями
с вероятностями ![]() . Тогда
. Тогда ![]() - дискретная случайная величина, принимающая значения
- дискретная случайная величина, принимающая значения ![]() с вероятностями
с вероятностями ![]() . Поэтому из определения (37.2) математического ожидания следует
. Поэтому из определения (37.2) математического ожидания следует
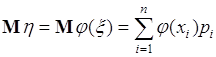 (37.3)
(37.3)
- выражение, определяющее математическое ожидание функции ![]() .
.
Математическим ожиданием непрерывной случайной величины ![]() с плотностью распределения вероятностей
с плотностью распределения вероятностей ![]() называется число
называется число
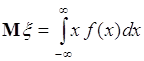 . (37.4)
. (37.4)
Аналогично определяется математическое ожидание случайной величины ![]() - как число
- как число
 , (37.5)
, (37.5)
где ![]() - однозначная функция одной переменной,
- однозначная функция одной переменной, ![]() - плотность распределения вероятностей случайной величины
- плотность распределения вероятностей случайной величины ![]() .
.
37.2. Определения (37.2) и (37.4) согласуются друг с другом. Соотношение (37.4) можно представить приближенно в виде интегральной суммы:
![]() , (37.6)
, (37.6)
где ![]() - малая величина. Тогда
- малая величина. Тогда ![]() , и следовательно, (37.4) формально представимо суммой (37.2).
, и следовательно, (37.4) формально представимо суммой (37.2).
Если ![]() - дискретная величина, принимающая значения
- дискретная величина, принимающая значения ![]() с вероятностями
с вероятностями ![]() , то ее плотность вероятности
, то ее плотность вероятности ![]() можно представить через
можно представить через ![]() - функцию:
- функцию:
 . (37.7)
. (37.7)
Подставим (37.7) в (37.4), тогда
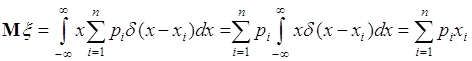 , (37.8)
, (37.8)
что совпадает с (37.2). Таким образом, определение (37.4) математического ожидания можно использовать как универсальное определение как для непрерывных, так и для дискретных случайных величин. Однако вычислять математическое ожидание дискретной случайной величины, конечно, удобнее по формуле (37.2).
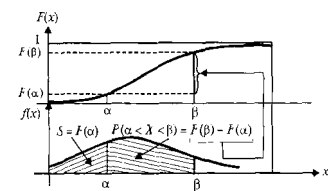
Выражение (37.4) можно представить через функцию распределения ![]() случайной величины
случайной величины ![]() . Для этого выполним следующие преобразования:
. Для этого выполним следующие преобразования: 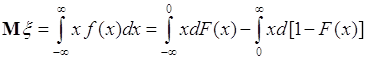 . Далее используем для вычисления интеграла способ «по частям»:
. Далее используем для вычисления интеграла способ «по частям»:
 .
.
Пусть функция ![]() удовлетворяет условиям:
удовлетворяет условиям: ![]() ,
, ![]() , тогда
, тогда
 . (37.9)
. (37.9)
Это выражение позволяет вычислять математическое ожидание ![]() через функцию распределения
через функцию распределения![]() .
.
Примеры вычисления математического ожидания случайной величины
38.1. Пусть гауссова случайная величина ![]() имеет плотность распределения вероятностей (35.4). Вычислим ее математическое ожидание. Для этого подставим выражение (35.4) в формулу (37.4), тогда
имеет плотность распределения вероятностей (35.4). Вычислим ее математическое ожидание. Для этого подставим выражение (35.4) в формулу (37.4), тогда
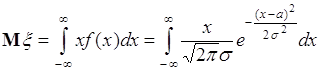 . (38.1)
. (38.1)
Вместо переменной интегрирования ![]() введем новую переменную
введем новую переменную ![]() ,
, ![]() , тогда
, тогда
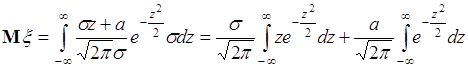 . (38.2)
. (38.2)
Функция ![]() является нечетной, поэтому интеграл в первом слагаемом (38.2) равен нулю. Во втором слагаемом
является нечетной, поэтому интеграл в первом слагаемом (38.2) равен нулю. Во втором слагаемом
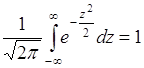 . (38.3)
. (38.3)
Это равенство представляет собой условие нормировки для гауссовой плотности распределения вероятностей (35.4) с параметрами: ![]() и
и ![]() . Таким образом, из (38.2) следует
. Таким образом, из (38.2) следует ![]() - среднее гауссовой случайной величины является параметром плотности распределения вероятностей (35.4). В данном случае
- среднее гауссовой случайной величины является параметром плотности распределения вероятностей (35.4). В данном случае ![]() имеет геометрическую интерпретацию (рис. 35.2) как значение аргумента
имеет геометрическую интерпретацию (рис. 35.2) как значение аргумента ![]() , при котором плотность (35.4) принимает максимальное значение. В дальнейшем символ
, при котором плотность (35.4) принимает максимальное значение. В дальнейшем символ ![]() используется также и для обозначения среднего любой случайной величины
используется также и для обозначения среднего любой случайной величины ![]() .
.
38.2. Вычислим среднее случайной величины ![]() , распределенной по экспоненциальному закону (35.8):
, распределенной по экспоненциальному закону (35.8):
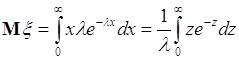 . (38.4)
. (38.4)
Далее используем способ интегрирования «по частям»:
 . (38.5)
. (38.5)
38.3. Пусть ![]() - число успехов в серии из
- число успехов в серии из ![]() независимых опытов. Тогда вероятности
независимых опытов. Тогда вероятности ![]() ,
, ![]() определяются формулой Бернули. Поэтому
определяются формулой Бернули. Поэтому
 . (38.6)
. (38.6)
Последнее равенство справедливо, поскольку ![]() . Подставим в (38.6) формулу Бернули, тогда:
. Подставим в (38.6) формулу Бернули, тогда:
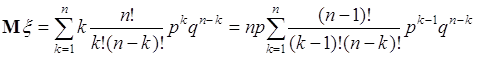 . (38.7)
. (38.7)
Введем новый индекс суммирования ![]() , тогда
, тогда
 . (38.8)
. (38.8)
Поскольку ![]() - вероятность
- вероятность ![]() успехов в серии из
успехов в серии из ![]() опытов, то
опытов, то  - как вероятность достоверного события, состоящего в появлении любого числа успехов в интервале
- как вероятность достоверного события, состоящего в появлении любого числа успехов в интервале ![]() . Поэтому из (38.8) следует
. Поэтому из (38.8) следует
![]() . (38.9)
. (38.9)
38.4. Однако не у всякой случайной величины существует ее математическое ожидание. Причиной этого является расходимость интеграла (37.4), что в свою очередь, обусловлено малой скоростью сходимости к нулю плотности ![]() при
при ![]() , так что для функции
, так что для функции ![]() не существует интеграл вида (37.4). Для примера рассмотрим вычисление математического ожидания случайной величины
не существует интеграл вида (37.4). Для примера рассмотрим вычисление математического ожидания случайной величины ![]() , распределенной по закону Коши:
, распределенной по закону Коши: 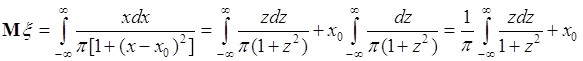 .
.
(38.10)
Здесь несобственный интеграл расходится, так как
 .
.
Следовательно, случайная величина ![]() не имеет математического ожидания. Однако, если интеграл в (38.10) понимать в смысле главного значения Коши, то
не имеет математического ожидания. Однако, если интеграл в (38.10) понимать в смысле главного значения Коши, то
 ,
,
поскольку функция ![]() является нечетной. Следовательно, при этом
является нечетной. Следовательно, при этом
![]() . (38.11)
. (38.11)
Свойства математического ожидания
Основные свойства математического ожидания следуют непосредственно из свойств интеграла в определении (37.5):
 . (39.1)
. (39.1)
1. Пусть ![]() представляет собой постоянную
представляет собой постоянную ![]() , тогда из (39.1) следует
, тогда из (39.1) следует
 , (39.2)
, (39.2)
поскольку для плотности ![]() выполняется условие нормировки (33.6). Таким образом, математическое ожидание постоянной равно самой постоянной.
выполняется условие нормировки (33.6). Таким образом, математическое ожидание постоянной равно самой постоянной.
2. Пусть ![]() , где
, где ![]() - число и
- число и ![]() - однозначная функция одной переменной, тогда из (39.1) следует
- однозначная функция одной переменной, тогда из (39.1) следует
 . (39.3)
. (39.3)
Таким образом, постоянный множитель ![]() можно вынести за знак математического ожидания.
можно вынести за знак математического ожидания.
3. Пусть ![]() , где
, где ![]() - числа,
- числа, ![]() - однозначные функции одной переменной, тогда из (39.1) следует
- однозначные функции одной переменной, тогда из (39.1) следует
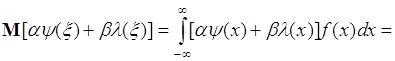
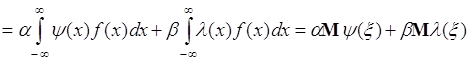 . (39.4)
. (39.4)
Из этого равенства при ![]() следует свойство 2, а при
следует свойство 2, а при ![]() и
и ![]() - свойство 1.
- свойство 1.
Математическое ожидание ![]() - это число, которое ставится в соответствие случайной величине
- это число, которое ставится в соответствие случайной величине ![]() . Поэтому
. Поэтому ![]() можно рассматривать как операцию (оператор, функцию) над случайной величиной
можно рассматривать как операцию (оператор, функцию) над случайной величиной ![]() . В соответствии со свойствами 1-3 оператор математического ожидания является линейным оператором.
. В соответствии со свойствами 1-3 оператор математического ожидания является линейным оператором.
40.1. Дисперсией случайной величины ![]() называется число
называется число
![]() . (40.1)
. (40.1)
Дисперсия является удобной характеристикой разброса значений ![]() около ее среднего значения
около ее среднего значения ![]() . Часто используется для обозначения дисперсии символ
. Часто используется для обозначения дисперсии символ ![]() . Тогда
. Тогда ![]() называется среднеквадратическим уклонением случайной величины
называется среднеквадратическим уклонением случайной величины ![]() . Если дисперсия имеет размерность квадрата случайной величины, то размерность
. Если дисперсия имеет размерность квадрата случайной величины, то размерность ![]() совпадает с размерностью случайной величины. Из (40.1) в соответствии со свойствами математического ожидания следует
совпадает с размерностью случайной величины. Из (40.1) в соответствии со свойствами математического ожидания следует
![]() . (40.2)
. (40.2)
Таким образом,
![]() . (40.3)
. (40.3)
Если ![]() дискретная случайная величина со значениями
дискретная случайная величина со значениями ![]() и соответствующими вероятностями
и соответствующими вероятностями ![]() , то ее дисперсия
, то ее дисперсия
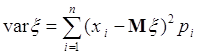 (40.4)
(40.4)
Если ![]() - непрерывная случайная величина и
- непрерывная случайная величина и ![]() - ее плотность вероятности, то
- ее плотность вероятности, то
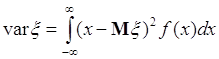 . (40.5)
. (40.5)
40.2. Рассмотрим примеры. Вычислим дисперсию нормальной случайной величины. Ее плотность ![]() определяется формулой (35.4). Подставим
определяется формулой (35.4). Подставим ![]() в (40.5), тогда
в (40.5), тогда
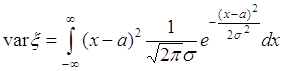 . (40.6)
. (40.6)
Пусть ![]() , тогда
, тогда ![]() ,
,
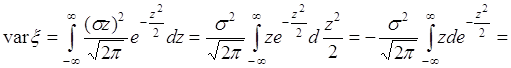
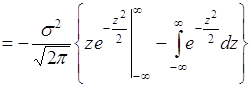 . (40.7)
. (40.7)
Подстановка пределов в (40.7) дает нулевые результаты, а интеграл равен ![]() . Поэтому
. Поэтому
![]() . (40.8)
. (40.8)
Таким образом, параметр ![]() в плотности нормальной случайной величины является дисперсией этой величины, а среднеквадратичное уклонение
в плотности нормальной случайной величины является дисперсией этой величины, а среднеквадратичное уклонение ![]() определяет эффективную ширину плотности
определяет эффективную ширину плотности ![]() : значение
: значение ![]() в
в ![]() раз меньше значения
раз меньше значения ![]() - в точке максимума.
- в точке максимума.
40.3. В некоторых случаях для вычисления дисперсии удобно использовать формулу (40.3). Например, для экспоненциально распределенной случайной величины ![]() плотность имеет вид (35.8), а ее среднее
плотность имеет вид (35.8), а ее среднее ![]() . Вычислим
. Вычислим
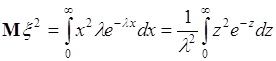 . (40.9)
. (40.9)
Интеграл в (40.9) вычисляется по частям:
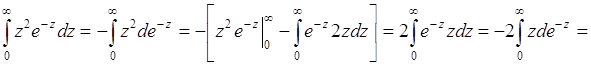
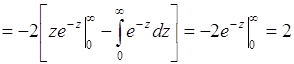 .
.
Таким образом, ![]() . Полученный результат подставим в формулу (40.3), тогда
. Полученный результат подставим в формулу (40.3), тогда
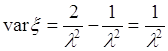 . 40.10)
. 40.10)
40.4. Вычислим дисперсию числа успехов в вероятностной схеме Бернулли, как пример вычисления дисперсии дискретной случайной величины. При этом также используем формулу (40.3), т.е. на первом шаге вычислим среднее от квадрата ![]() , а затем используя ранее полученный результат, дисперсию по формуле (40.3). Итак, среднее от квадрата
, а затем используя ранее полученный результат, дисперсию по формуле (40.3). Итак, среднее от квадрата
 , (40.11)
, (40.11)
где ![]() - распределение вероятностей Бернулли, поэтому
- распределение вероятностей Бернулли, поэтому
 . (40.12)
. (40.12)
Пусть ![]() , тогда
, тогда ![]() и
и
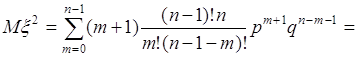
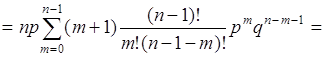
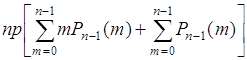 .(40.13)
.(40.13)
Здесь ![]() - вероятность появления
- вероятность появления ![]() успехов в последовательности из
успехов в последовательности из ![]() опытов. Поэтому
опытов. Поэтому  , как вероятность достоверного события, состоящего в том, что число успехов будет любым в интервале от
, как вероятность достоверного события, состоящего в том, что число успехов будет любым в интервале от ![]() до
до ![]() . Первая сумма в (40.13)
. Первая сумма в (40.13) 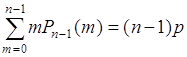 как математическое ожидание числа успехов в последовательности из
как математическое ожидание числа успехов в последовательности из ![]() опытов в соответствии с формулой (38.9). Подставим эти результаты в (40.13), тогда
опытов в соответствии с формулой (38.9). Подставим эти результаты в (40.13), тогда
![]() . (40.14)
. (40.14)
Теперь
![]() . (40.15)
. (40.15)
Похожие работы
... . Г. Моделирование случайной величины с нормальным распределением. Случайная величина имеет нормальный закон распределения, если ее функция распределения имеет вид: , где и — параметры. Для компьютерного моделирования случайной величины с нормальным законом распределения можно использовать как метод обратных функций, так и метод, специально разработанный для нормального закона. Согласно ...
... , очень мала и равна 0,0027. Такие события считаются практически невозможными. В этом и состоит правило «трех сигм»: если случайная величина распределена по нормальному закону, то ее отклонение от математического ожидания практически не превышает±3σ. Понятие о теоремах, относящихся к группе «центральной предельной теоремы» В теоремах этой группы выясняются условия, при которых возникает ...
... критических точек распределения ([1], стр. 465), по уровню значимости =0,05 и числу степеней свободы 8-3=5 находим Т.к. , экспериментальные данные не противоречат гипотезе и о нормальном распределении случайной величины . Для случайной величины : Используя предполагаемый закон распределения, вычислим теоретические частоты по формуле , где - объем выборки, - шаг (разность между ...
... Впрочем, для наиболее распространённых псевдослучайных чисел период столь велик, что превосходит любые практические потребности. Подавляющее большинство расчётов по методу Монте-Карло осуществляется с использованием псевдослучайных чисел. Значения любой случайной величины можно получить путём преобразования значений одной какой-либо случайной величины. Обычно роль такой случайной величины играет ...


0 комментариев