Навигация
Случайные величины
Оглавление
Случайные величины.. 2
Функция распределения вероятностей.. 3
Основные свойства функции распределения вероятностей.. 5
Функция распределения вероятностей дискретной случайной величины 6
Плотность распределения вероятностей.. 7
Плотность распределения вероятностей дискретной случайной величины 9
Примеры плотностей и функций распределения вероятностей.. 10
Сингулярные случайные величины.. 13
Математическое ожидание случайной величины.. 15
Примеры вычисления математического ожидания случайной величины.. 17
Свойства математического ожидания. 19
Дисперсия случайной величины.. 20
Моменты случайной величины.. 22
Неравенство Чебышева. 23
Коэффициент асимметрии.. 25
Коэффициент эксцесса. 26
Среднеквадратическая ошибка. 27
Характеристическая функция. 28
Основные свойства характеристической функции.. 29
Примеры вычисления характеристической функции.. 30
Моменты, кумулянты и характеристическая функция. 31
Случайные величины
Выше рассматривались эксперименты, результаты которых являются случайными событиями. Однако часто возникает необходимость количественного представления результатов эксперимента в виде некоторой величины ![]() , которая называется случайной величиной. Случайная величина является вторым (после случайного события) основным объектом изучения теории вероятностей и обеспечивает более общий способ описания опыта со случайным исходом, чем совокупность случайных событий.
, которая называется случайной величиной. Случайная величина является вторым (после случайного события) основным объектом изучения теории вероятностей и обеспечивает более общий способ описания опыта со случайным исходом, чем совокупность случайных событий.
Рассматривая эксперименты со случайным исходом, мы уже имели дело со случайными величинами. Так, число успехов ![]() в серии из
в серии из ![]() испытаний - пример случайной величины. Другими примерами случайных величин являются: число вызовов на телефонной станции за единицу времени; время ожидания очередного вызова; число частиц с заданной энергией в системах частиц, рассматриваемых в статистической физике; средняя суточная температура в данной местности и т.д.
испытаний - пример случайной величины. Другими примерами случайных величин являются: число вызовов на телефонной станции за единицу времени; время ожидания очередного вызова; число частиц с заданной энергией в системах частиц, рассматриваемых в статистической физике; средняя суточная температура в данной местности и т.д.
Случайная величина характерна тем, что невозможно точно предсказать ее значение, которое она примет, но с другой стороны, множество ее возможных значений обычно известно. Так для числа успехов в последовательности из ![]() испытаний это множество конечно, поскольку число успехов может принимать значения
испытаний это множество конечно, поскольку число успехов может принимать значения ![]() . Множество значений случайной величины, может совпадать с вещественной полуосью
. Множество значений случайной величины, может совпадать с вещественной полуосью ![]() , как в случае времени ожидания и т.д.
, как в случае времени ожидания и т.д.
Рассмотрим примеры экспериментов со случайным исходом, для описания которых обычно применяются случайные события и введем эквивалентное описание с помощью задания случайной величины.
1). Пусть результатом опыта может быть событие ![]() или событие
или событие ![]() . Тогда этому эксперименту можно поставить в соответствие случайную величину
. Тогда этому эксперименту можно поставить в соответствие случайную величину ![]() , которая принимает два значения, например,
, которая принимает два значения, например, ![]() и
и ![]() с вероятностями
с вероятностями ![]() и
и ![]() , причем имеют место равенства:
, причем имеют место равенства: ![]() и
и ![]() . Таким образом, опыт характеризуется двумя исходами
. Таким образом, опыт характеризуется двумя исходами ![]() и
и![]() с вероятностями
с вероятностями ![]() и
и ![]() , или этот же опыт характеризуется случайной величиной
, или этот же опыт характеризуется случайной величиной ![]() , принимающей два значения
, принимающей два значения ![]() и
и ![]() с вероятностями
с вероятностями ![]() и
и ![]() .
.
2). Рассмотрим опыт с бросанием игральной кости. Здесь исходом опыта может быть одно из событий ![]() , где
, где ![]() - выпадение грани с номером
- выпадение грани с номером ![]() . Вероятности
. Вероятности ![]() ,
, ![]() . Введем эквивалентное описание этого опыта с помощью случайной величины
. Введем эквивалентное описание этого опыта с помощью случайной величины ![]() , которая может принимать значения
, которая может принимать значения ![]() с вероятностями
с вероятностями ![]() ,
, ![]() .
.
3). Последовательность ![]() независимых испытаний характеризуется полной группой несовместных событий
независимых испытаний характеризуется полной группой несовместных событий ![]() , где
, где ![]() - событие, состоящее в появлении
- событие, состоящее в появлении ![]() успехов в серии из
успехов в серии из ![]() опытов; причем вероятность события
опытов; причем вероятность события ![]() определяется формулой Бернули, т.е.
определяется формулой Бернули, т.е. ![]() . Здесь можно ввести случайную величину
. Здесь можно ввести случайную величину ![]() - число успехов, которая принимает значения
- число успехов, которая принимает значения ![]() с вероятностями
с вероятностями ![]() . Таким образом, последовательность независимых испытаний характеризуется случайными событиями
. Таким образом, последовательность независимых испытаний характеризуется случайными событиями ![]() с их вероятностями
с их вероятностями ![]() или случайной величиной
или случайной величиной ![]() с вероятностями того, что
с вероятностями того, что ![]() принимает значения
принимает значения ![]() :
: ![]() ,
, ![]() .
.
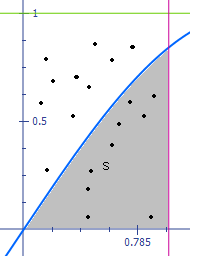
4). Однако, не для всякого опыта со случайным исходом существует столь простое соответствие между случайной величиной и совокупностью случайных событий. К примеру, рассмотрим эксперимент, в котором точка наугад бросается на отрезок ![]() . Здесь естественно ввести случайную величину
. Здесь естественно ввести случайную величину ![]() - координату на отрезке
- координату на отрезке ![]() , в которую попадает точка. Таким образом, можно говорить о случайном событии
, в которую попадает точка. Таким образом, можно говорить о случайном событии ![]() , где
, где ![]() - число из
- число из ![]() . Однако вероятность этого события
. Однако вероятность этого события ![]() . Можно поступить иначе - отрезок
. Можно поступить иначе - отрезок ![]() разбить на конечное число непересекающихся отрезков
разбить на конечное число непересекающихся отрезков ![]() и рассматривать случайные события, состоящие в том, что случайная величина
и рассматривать случайные события, состоящие в том, что случайная величина ![]() принимает значения из интервала
принимает значения из интервала ![]() . Тогда вероятности
. Тогда вероятности ![]() - конечные величины. Однако и этот способ имеет существенный недостаток, поскольку отрезки
- конечные величины. Однако и этот способ имеет существенный недостаток, поскольку отрезки ![]() выбираются произвольным образом. Для того, чтобы устранить этот недостаток рассматривают отрезки вида
выбираются произвольным образом. Для того, чтобы устранить этот недостаток рассматривают отрезки вида ![]() , где переменная
, где переменная ![]() . Тогда соответствующая вероятность
. Тогда соответствующая вероятность
![]() (29.1)
(29.1)
является функцией аргумента ![]() . Это усложняет математическое описание случайной величины, но при этом описание (29.1) становится единственным, устраняется неоднозначность выбора отрезков
. Это усложняет математическое описание случайной величины, но при этом описание (29.1) становится единственным, устраняется неоднозначность выбора отрезков ![]() .
.
Для каждого из рассмотренных примеров несложно определить вероятностное пространство ![]() , где
, где ![]() - пространство элементарных событий,
- пространство элементарных событий, ![]() -
- ![]() - алгебра событий (подмножеств
- алгебра событий (подмножеств ![]() ),
), ![]() - вероятность, определенная для любого
- вероятность, определенная для любого ![]() . Например, в последнем примере
. Например, в последнем примере ![]() ,
, ![]() -
- ![]() - алгебра всех отрезков
- алгебра всех отрезков ![]() , содержащихся в
, содержащихся в ![]() .
.
Рассмотренные примеры приводят к следующему определению случайной величины.
Пусть ![]() - вероятностное пространство. Случайной величиной
- вероятностное пространство. Случайной величиной ![]() называется однозначная действительная функция
называется однозначная действительная функция ![]() , определенная на
, определенная на ![]() , для которой множество элементарных событий вида
, для которой множество элементарных событий вида ![]() является событием (т.е. принадлежат
является событием (т.е. принадлежат ![]() ) для каждого действительного числа
) для каждого действительного числа ![]() .
.
Таким образом, в определении требуется, чтобы для каждого вещественного ![]() множество
множество ![]() , и это условие гарантирует, что для каждого
, и это условие гарантирует, что для каждого ![]() определена вероятность события
определена вероятность события ![]() . Это событие принято обозначать более краткой записью
. Это событие принято обозначать более краткой записью ![]() .
.
Функция
![]() ,
, ![]() , (30.1)
, (30.1)
называется функцией распределения вероятностей случайной величины ![]() .
.
Функция ![]() иногда называется кратко – функция распределения, а также – интегральным законом распределения вероятностей случайной величины
иногда называется кратко – функция распределения, а также – интегральным законом распределения вероятностей случайной величины ![]() . Функция
. Функция ![]() является полной характеристикой случайной величины, то есть представляет собой математическое описание всех свойств случайной величины и более детального способа описания этих свойств не существует.
является полной характеристикой случайной величины, то есть представляет собой математическое описание всех свойств случайной величины и более детального способа описания этих свойств не существует.
Отметим следующую важную особенность определения (30.1). Часто функцию ![]() определяют иначе:
определяют иначе:
![]() ,
, ![]() . (30.2)
. (30.2)
Согласно (30.1) функция ![]() является непрерывной справа. Этот вопрос подробнее будет рассмотрен ниже. Если же использовать определение (30.2), то
является непрерывной справа. Этот вопрос подробнее будет рассмотрен ниже. Если же использовать определение (30.2), то ![]() - непрерывна слева, что является следствием применения строгого неравенства в соотношении (30.2). Функции (30.1) и (30.2) представляют собой эквивалентные описания случайной величины, поскольку не имеет значения каким определением пользоваться как при изучении теоретических вопросов, так и при решении задач. Для определенности в дальнейшем будем использовать только определение (30.1).
- непрерывна слева, что является следствием применения строгого неравенства в соотношении (30.2). Функции (30.1) и (30.2) представляют собой эквивалентные описания случайной величины, поскольку не имеет значения каким определением пользоваться как при изучении теоретических вопросов, так и при решении задач. Для определенности в дальнейшем будем использовать только определение (30.1).
Рассмотрим пример построения графика функции ![]() . Пусть случайная величина
. Пусть случайная величина ![]() принимает значения
принимает значения ![]() ,
, ![]() ,
, ![]() с вероятностями
с вероятностями ![]() ,
, ![]() , причем
, причем ![]() . Таким образом, другие значения кроме указанных данная случайная величина принимает с нулевой вероятностью:
. Таким образом, другие значения кроме указанных данная случайная величина принимает с нулевой вероятностью: ![]() , для любого
, для любого ![]() ,
, ![]() . Или как говорят, других значений кроме
. Или как говорят, других значений кроме ![]() ,
, ![]() ,
, ![]() случайная величина
случайная величина ![]() не может принимать. Пусть для определенности
не может принимать. Пусть для определенности ![]() . Найдем значения функции
. Найдем значения функции ![]() для
для ![]() из интервалов: 1)
из интервалов: 1) ![]() , 2)
, 2) ![]() , 3)
, 3) ![]() , 4)
, 4) ![]() , 5)
, 5) ![]() , 6)
, 6) ![]() , 7)
, 7) ![]() . На первом интервале
. На первом интервале ![]() , поэтому функция распределения
, поэтому функция распределения ![]() . 2). Если
. 2). Если ![]() , то
, то ![]() . Очевидно случайные события
. Очевидно случайные события ![]() и
и ![]() несовместны, поэтому по формуле сложения вероятностей
несовместны, поэтому по формуле сложения вероятностей ![]() . По условию событие
. По условию событие ![]() невозможное и
невозможное и ![]() , а
, а ![]() . Поэтому
. Поэтому ![]() . 3). Пусть
. 3). Пусть ![]() , тогда
, тогда ![]() . Здесь первое слагаемое
. Здесь первое слагаемое ![]() , а второе
, а второе ![]() , поскольку событие
, поскольку событие ![]() - невозможное. Таким образом
- невозможное. Таким образом ![]() для любого
для любого ![]() ,
удовлетворяющего условию
,
удовлетворяющего условию ![]() . 4). Пусть
. 4). Пусть ![]() , тогда
, тогда ![]() . 5). Если
. 5). Если ![]() , то
, то ![]() . 6) При
. 6) При ![]() имеем
имеем ![]() . 7) Если
. 7) Если ![]() , то
, то ![]() . Результаты вычислений представлены на рис. 30.1 графиком функции
. Результаты вычислений представлены на рис. 30.1 графиком функции ![]() . В точках разрыва
. В точках разрыва ![]() ,
, ![]() ,
, ![]() указана непрерывность функции справа.
указана непрерывность функции справа.
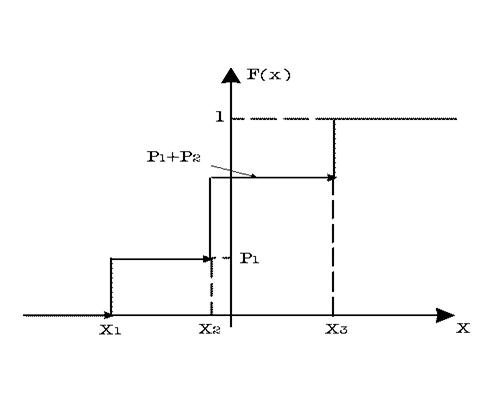
Рис. 30.1. График функции распределения вероятностей.
Основные свойства функции распределения вероятностейРассмотрим основные свойства функции распределения, следующие непосредственно из определения:
![]() . (31.1)
. (31.1)
1. Введем обозначение: ![]() . Тогда из определения следует
. Тогда из определения следует ![]() . Здесь выражение
. Здесь выражение ![]() рассматривается как невозможное событие с нулевой вероятностью.
рассматривается как невозможное событие с нулевой вероятностью.
2. Пусть ![]() . Тогда из определения функции
. Тогда из определения функции ![]() следует
следует ![]() . Случайное событие
. Случайное событие ![]() является достоверным и его вероятность равна единице.
является достоверным и его вероятность равна единице.
3. Вероятность ![]() случайного события
случайного события ![]() , состоящего в том, что случайная величина
, состоящего в том, что случайная величина ![]() принимает значение из интервала
принимает значение из интервала ![]() при
при ![]() определяется через функцию
определяется через функцию ![]() следующим равенством
следующим равенством
![]() . (31.2)
. (31.2)
Для доказательства этого равенства рассмотрим соотношение
![]() . (31.3)
. (31.3)
События ![]() и
и ![]() несовместны, поэтому по формуле сложения вероятностей из (31.3) следует
несовместны, поэтому по формуле сложения вероятностей из (31.3) следует
![]() , (31.4)
, (31.4)
что и совпадает с формулой (31.2), поскольку ![]() и
и ![]() .
.
4. Функция ![]() является неубывающей. Для доказательства рассмотрим
является неубывающей. Для доказательства рассмотрим ![]() . При этом справедливо равенство (31.2). Его левая часть
. При этом справедливо равенство (31.2). Его левая часть ![]() , поскольку вероятность принимает значения из интервала
, поскольку вероятность принимает значения из интервала ![]() . Поэтому и правая часть равенства (31.2) неотрицательна:
. Поэтому и правая часть равенства (31.2) неотрицательна: ![]() , или
, или ![]() . Это равенство получено при условии
. Это равенство получено при условии ![]() , поэтому
, поэтому ![]() - неубывающая функция.
- неубывающая функция.
5. Функция ![]() непрерывна справа в каждой точке
непрерывна справа в каждой точке![]() , т.е.
, т.е.
![]() , (31.5)
, (31.5)
где ![]() - любая последовательность, стремящаяся к
- любая последовательность, стремящаяся к ![]() справа, т.е.
справа, т.е. ![]() и
и ![]() .
.
Для доказательства представим функцию ![]() в виде:
в виде: ![]()
![]() . (31.5)
. (31.5)
Отсюда
![]() . (31.6)
. (31.6)
Теперь на основании аксиомы счетной аддитивности вероятности выражение в фигурных скобках равно ![]() , таким образом
, таким образом ![]()
![]() , что и доказывает непрерывность справа функции
, что и доказывает непрерывность справа функции ![]() .
.
Таким образом, каждая функция распределения вероятностей обладает свойствами 1-5. Верно и обратное утверждение: если ![]() ,
, ![]() , удовлетворяет условиям 1-5 ,то она может рассматриваться как функция распределения некоторой случайной величины.
, удовлетворяет условиям 1-5 ,то она может рассматриваться как функция распределения некоторой случайной величины.
Случайная величина ![]() называется дискретной, если множество ее значений конечно или счетно.
называется дискретной, если множество ее значений конечно или счетно.
Для полного вероятностного описания дискретной случайной величины ![]() , принимающей значения
, принимающей значения ![]() , достаточно задать вероятности
, достаточно задать вероятности
![]() ,
, ![]() (32.1)
(32.1)
того, что случайная величина ![]() принимает значение
принимает значение ![]() . Если заданы
. Если заданы ![]() и
и ![]() ,
, ![]() , тогда функцию распределения вероятностей
, тогда функцию распределения вероятностей ![]() дискретной случайной величины
дискретной случайной величины ![]() можно представить в виде:
можно представить в виде:
![]() . (32.2)
. (32.2)
Здесь суммирование ведется по всем индексам ![]() , удовлетворяющим условию:
, удовлетворяющим условию: ![]() .
.
Функцию распределения вероятностей дискретной случайной величины иногда представляют через так называемую функцию единичного скачка
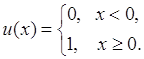 (32.3)
(32.3)
При этом ![]() принимает вид
принимает вид
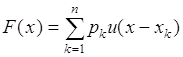 , (32.4)
, (32.4)
если случайная величина ![]() принимает конечное множество значений
принимает конечное множество значений ![]() , и верхний предел суммирования в (32.4) полагается равным
, и верхний предел суммирования в (32.4) полагается равным ![]() , если случайная величина принимает счетное множество значений.
, если случайная величина принимает счетное множество значений.
Пример построения графика функций распределения вероятностей дискретной случайной величины был рассмотрен в п.30.
Плотность распределения вероятностей
Пусть случайная величина ![]() имеет дифференцируемую функцию распределению вероятностей
имеет дифференцируемую функцию распределению вероятностей ![]() , тогда функция
, тогда функция
![]() (33.1)
(33.1)
называется плотностью распределения вероятностей ( или плотностью вероятности) случайной величины ![]() , а случайная величина
, а случайная величина ![]() - непрерывной случайной величиной.
- непрерывной случайной величиной.
Рассмотрим основные свойства плотности вероятности.
Из определения производной следует равенство:
![]() . (33.2)
. (33.2)
Согласно свойствам функции ![]() имеет место равенство
имеет место равенство ![]() . Поэтому (33.2) принимает вид:
. Поэтому (33.2) принимает вид:
![]() . (33.3)
. (33.3)
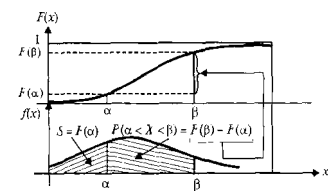
Это соотношение объясняет название функции ![]() . Действительно, согласно (33.3) функция
. Действительно, согласно (33.3) функция ![]() - это вероятность
- это вероятность ![]() , приходящаяся на единицу интервала
, приходящаяся на единицу интервала ![]() , в точке
, в точке ![]() , поскольку
, поскольку ![]() . Таким образом, плотность вероятности, определяемая соотношением (33.3), аналогична определениям плотностей других величин, известных в физике, таких как плотность тока, плотность вещества, плотность заряда и т.д.
. Таким образом, плотность вероятности, определяемая соотношением (33.3), аналогична определениям плотностей других величин, известных в физике, таких как плотность тока, плотность вещества, плотность заряда и т.д.
2. Поскольку ![]() - неубывающая функция, то ее производная
- неубывающая функция, то ее производная ![]() - функция неотрицательная:
- функция неотрицательная:
![]() . (33.4)
. (33.4)
Похожие работы
... . Г. Моделирование случайной величины с нормальным распределением. Случайная величина имеет нормальный закон распределения, если ее функция распределения имеет вид: , где и — параметры. Для компьютерного моделирования случайной величины с нормальным законом распределения можно использовать как метод обратных функций, так и метод, специально разработанный для нормального закона. Согласно ...
... , очень мала и равна 0,0027. Такие события считаются практически невозможными. В этом и состоит правило «трех сигм»: если случайная величина распределена по нормальному закону, то ее отклонение от математического ожидания практически не превышает±3σ. Понятие о теоремах, относящихся к группе «центральной предельной теоремы» В теоремах этой группы выясняются условия, при которых возникает ...
... критических точек распределения ([1], стр. 465), по уровню значимости =0,05 и числу степеней свободы 8-3=5 находим Т.к. , экспериментальные данные не противоречат гипотезе и о нормальном распределении случайной величины . Для случайной величины : Используя предполагаемый закон распределения, вычислим теоретические частоты по формуле , где - объем выборки, - шаг (разность между ...
... Впрочем, для наиболее распространённых псевдослучайных чисел период столь велик, что превосходит любые практические потребности. Подавляющее большинство расчётов по методу Монте-Карло осуществляется с использованием псевдослучайных чисел. Значения любой случайной величины можно получить путём преобразования значений одной какой-либо случайной величины. Обычно роль такой случайной величины играет ...


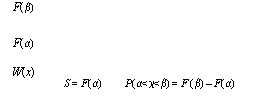
0 комментариев