Навигация
4. Аналогично из (61.6)
 . (61.8)
. (61.8)
5. Условие нормировки для плотности вероятности ![]() также следует из соотношения (61.6):
также следует из соотношения (61.6):
 . (61.9)
. (61.9)
6. Пусть ![]() - область
- область ![]() - мерного пространства, тогда
- мерного пространства, тогда ![]() - вероятность того, что
- вероятность того, что ![]() - мерный случайный вектор принимает значение из области
- мерный случайный вектор принимает значение из области ![]() , определяется через плотность
, определяется через плотность ![]() :
:
 . (61.10)
. (61.10)
Доказательство этого соотношения следует из (61.6) с учетом того, что любая область ![]() может быть покрыта
может быть покрыта ![]() - мерными параллелепипедами при условии, что
- мерными параллелепипедами при условии, что ![]() - наибольшая сторона параллелепипеда стремится к нулю.
- наибольшая сторона параллелепипеда стремится к нулю.
7. Для любого ![]()
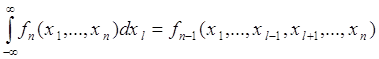 . (61.11)
. (61.11)
Это равенство называется свойством согласованности плотности: из плотности вероятности порядка ![]() путем интегрирования по «лишнему» аргументу
путем интегрирования по «лишнему» аргументу ![]() может быть получена плотность вероятности порядка
может быть получена плотность вероятности порядка ![]() . Для доказательства представим обе части равенства (60.5) через плотности, используя (61.8), тогда (60.5) принимает вид:
. Для доказательства представим обе части равенства (60.5) через плотности, используя (61.8), тогда (60.5) принимает вид:

 . (61.12)
. (61.12)
Продифференцируем обе части этого равенства по аргументам ![]() , что приводит к выражению (61.11).
, что приводит к выражению (61.11).
Многомерное нормальное распределение
Случайный вектор ![]() называется нормально распределенным, если его плотность вероятности
называется нормально распределенным, если его плотность вероятности
 , (62.1)
, (62.1)
где ![]() ;
; ![]() - ковариационная матрица вектора
- ковариационная матрица вектора ![]() , элемент которой
, элемент которой ![]() является ковариацией случайных величин
является ковариацией случайных величин ![]() ;
; ![]() - определитель матрицы
- определитель матрицы ![]() ;
; ![]() - матрица, обратная ковариационной.
- матрица, обратная ковариационной.
Рассмотрим плотность вероятности ![]() в частном случае попарно некоррелированных случайных величин
в частном случае попарно некоррелированных случайных величин ![]() , для которых выполняется условие
, для которых выполняется условие
![]() , (62.2)
, (62.2)
где ![]() - символ Кронекера. Таким образом, ковариационная матрица
- символ Кронекера. Таким образом, ковариационная матрица ![]() является диагональной, поскольку ее элементы (62.2) на главной диагонали – ненулевые, а вне главной диагонали - нулевые. Следовательно, определитель
является диагональной, поскольку ее элементы (62.2) на главной диагонали – ненулевые, а вне главной диагонали - нулевые. Следовательно, определитель
 . (62.3)
. (62.3)
Элемент ![]() матрицы
матрицы ![]() , обратной ковариационной можно найти по известной формуле:
, обратной ковариационной можно найти по известной формуле:
 , (62.4)
, (62.4)
где ![]() - алгебраическое дополнение элемента
- алгебраическое дополнение элемента ![]() матрицы
матрицы ![]() . Из (62.3) следует
. Из (62.3) следует
 , (62.5)
, (62.5)
а также ![]() при
при ![]() . Подстановка этих результатов в (62.4) приводит к выражению
. Подстановка этих результатов в (62.4) приводит к выражению
 . (62.6)
. (62.6)
Подставим (62.3), (62.6) в (62.1), тогда

 , (62.7)
, (62.7)
где ![]() - плотность вероятности случайной величины
- плотность вероятности случайной величины ![]() . Таким образом, для гауссова случайного вектора
. Таким образом, для гауссова случайного вектора ![]() из условия попарной некоррелированности его компонент
из условия попарной некоррелированности его компонент ![]() ,
, ![]() , следует условие (62.7) - независимости компонент случайного вектора.
, следует условие (62.7) - независимости компонент случайного вектора.
63.1 Функция ![]() переменных
переменных
![]() (63.1)
(63.1)
называется характеристической функцией случайного вектора ![]() .
.
Если случайный вектор ![]() является непрерывным, то его характеристическая функция (63.1) определяется через его плотность
является непрерывным, то его характеристическая функция (63.1) определяется через его плотность ![]() :
:
 . (63.2)
. (63.2)
Это соотношение является ![]() - мерным преобразованием Фурье от функции
- мерным преобразованием Фурье от функции ![]() . Поэтому плотность
. Поэтому плотность ![]() можно выразить через характеристическую функцию
можно выразить через характеристическую функцию ![]() в виде обратного преобразования Фурье по отношению к (63.2):
в виде обратного преобразования Фурье по отношению к (63.2):
 . (63.3)
. (63.3)
Похожие работы
... математического ожидания. Таким образом, (72.6) принимает вид . (72.7) 72.2. Функции вида , (72.8) где целые числа , называются начальными моментами порядка случайного процесса . Аналогично центральные моменты определяются соотношениями: . (72.9) Для функций (72.8), (72.9) используется общее название - моментные функции. Наиболее простые ...
... damn(t)/dt =[daij(t)/dt] 1.3 ПОНЯТИЕ ДИНАМЧЕСКОГО ОБЬЕКТА. Физический объект - физическое устройство, характеризуемое некоторым числом свойств, соответствующих целям его использования. В теории систем существенным является не физическое, а математическое описание свойств объекта и соотношений между ними. В теории систем объектом А является абстрактный объект, связанный с множеством ...
... проверить знания студента из первой части курса, которая излагается в первых четырёх модулях. Во вторых вопросах билета проверяются знания классической предельной проблемы теории вероятностей и математической статистики, которые излагаются в следующих пяти модулях. 1. Вероятностная модель с не более чем счётным числом элементарных исходов. Пример: испытания с равновозможными исходами. 2. ...
... несколько уравнений, а в каждом уравнении - несколько переменных. Задача оценивания параметров такой разветвленной модели решается с помощью сложных и причудливых методов. Однако все они имеют одну и ту же теоретическую основу. Поэтому для получения начального представления о содержании эконометрических методов мы ограничимся в последующих параграфах рассмотрением простой линейной регрессии. ...




0 комментариев