Навигация
54.2. Аналогично (54.2) числа
 (54.5)
(54.5)
называются центральными смешанными моментами, порядка ![]() . Наиболее важной групповой характеристикой двух случайных величин среди чисел (54.5) является ковариация
. Наиболее важной групповой характеристикой двух случайных величин среди чисел (54.5) является ковариация
 , (54.6)
, (54.6)
которая является центральным смешанным моментом порядка ![]() . Для ковариации используется также обозначение:
. Для ковариации используется также обозначение: ![]() . Если
. Если ![]() , то
, то ![]() - совпадает с дисперсией случайной величины
- совпадает с дисперсией случайной величины ![]() .
.
Если ![]() и
и ![]() - независимы, то из (54.6) следует, что ковариация
- независимы, то из (54.6) следует, что ковариация
![]() .
.
Обратное утверждение в общем случае неверно, т.е. из равенства ![]() в общем не следует независимость случайных величин
в общем не следует независимость случайных величин ![]() и
и ![]() . В частности, обратное утверждение справедливо, если
. В частности, обратное утверждение справедливо, если ![]() и
и ![]() - гауссовы случайные величины. Более подробно этот вопрос обсуждается ниже.
- гауссовы случайные величины. Более подробно этот вопрос обсуждается ниже.
54.3. Найдем связь между корреляцией ![]() и ковариацией
и ковариацией ![]() случайных величин
случайных величин ![]() и
и ![]() . Из определения ковариации (54.6) следует
. Из определения ковариации (54.6) следует
![]()
![]() .
.
Таким образом, ковариация ![]() и корреляция
и корреляция ![]() связаны соотношением
связаны соотношением
![]() . (54.7)
. (54.7)
55.1. Пусть случайные величины ![]() и
и ![]() имеют математические ожидания
имеют математические ожидания ![]() ,
, ![]() , дисперсии
, дисперсии ![]() ,
, ![]() , корреляцию
, корреляцию ![]() и ковариацию
и ковариацию ![]() . Рассмотрим неравенство
. Рассмотрим неравенство
 . (55.1)
. (55.1)
Возведем в квадрат, затем оператором математического ожидания подействуем на каждое слагаемое, тогда (55.1) принимает вид:
 ,
,
что далее сводится к неравенству
![]() . (55.2)
. (55.2)
Его левая часть ![]() может быть как положительной так и отрицательной, правая часть - только положительна. Поэтому неравенство (55.2) обычно записывается в более сильном варианте:
может быть как положительной так и отрицательной, правая часть - только положительна. Поэтому неравенство (55.2) обычно записывается в более сильном варианте:
![]() . (55.3)
. (55.3)
Таким образом, корреляция ![]() случайных величин
случайных величин ![]() и
и ![]() принимает значения из интервала
принимает значения из интервала ![]() .
.
Соотношение, аналогичное (55.3) можно получить и для ковариации ![]() , если в исходном выражении (55.1) вместо
, если в исходном выражении (55.1) вместо ![]() подставить центрированную случайную величину
подставить центрированную случайную величину ![]() и вместо
и вместо ![]() соответственно
соответственно ![]() . При этом необязательно выполнять все преобразования, аналогичные (55.1) - (55.3), достаточно учесть, что замена
. При этом необязательно выполнять все преобразования, аналогичные (55.1) - (55.3), достаточно учесть, что замена ![]() и
и ![]() приводит к замене
приводит к замене ![]() на
на ![]() ,
, ![]() на
на ![]() , а также
, а также ![]() на
на ![]() . Поэтому из (55.3) следует
. Поэтому из (55.3) следует
![]() . (55.4)
. (55.4)
55.2. Неравенства, определяющие область значений корреляции ![]() и ковариации
и ковариации ![]() , аналогичные (55.3), (55.4), можно получить в другом виде на основе следующего очевидного неравенства:
, аналогичные (55.3), (55.4), можно получить в другом виде на основе следующего очевидного неравенства:
![]() . (55.5)
. (55.5)
Отсюда ![]() , поэтому справедливо неравенство
, поэтому справедливо неравенство
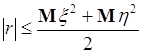 . (55.6)
. (55.6)
Если в (55.5) ![]() заменить соответственно на
заменить соответственно на ![]() и
и ![]() , то в (55.6)
, то в (55.6) ![]() заменяется на
заменяется на ![]() ,
, ![]() на
на ![]() и
и ![]() на
на ![]() . Поэтому (55.6) принимает вид:
. Поэтому (55.6) принимает вид:
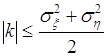 . (55.7)
. (55.7)
Для независимых случайных величин ![]() и
и ![]() ковариация
ковариация ![]() . В отличие от этого рассмотрим другой крайний случай, когда случайные величины
. В отличие от этого рассмотрим другой крайний случай, когда случайные величины ![]() и
и ![]() связаны функциональной зависимостью:
связаны функциональной зависимостью:
![]() , (56.1)
, (56.1)
где ![]() - числа. Вычислим ковариацию
- числа. Вычислим ковариацию ![]() случайных величин
случайных величин ![]() и
и ![]() :
:
![]() . (56.2)
. (56.2)
Из (56.1) следует ![]() . Подставим этот результат в (56.2), тогда
. Подставим этот результат в (56.2), тогда
![]() . (56.3)
. (56.3)
Из (56.1) определим дисперсию
![]() , (56.4)
, (56.4)
откуда ![]() . Это равенство подставим в (56.3), тогда
. Это равенство подставим в (56.3), тогда
 (56.5)
(56.5)
Таким образом, ковариация линейно связанных случайных величин ![]() и
и ![]() принимает максимальное значение
принимает максимальное значение ![]() , если
, если ![]() , или минимальное значение
, или минимальное значение ![]() , если
, если ![]() , на отрезке
, на отрезке ![]() допустимых значений для
допустимых значений для ![]() в общем случае (согласно формуле (55.4)).
в общем случае (согласно формуле (55.4)).
В связи с этим
можно выдвинуть предположение о том, что ковариация ![]() является мерой статистической связи между случайными величинами
является мерой статистической связи между случайными величинами ![]() и
и ![]() . Действительно, для двух крайних случаев получены подходящие для этого результаты, а именно: для независимых величин
. Действительно, для двух крайних случаев получены подходящие для этого результаты, а именно: для независимых величин ![]() , а для линейно связанных
, а для линейно связанных ![]() максимален. Далее будет показано, что это предположение верно, но не в общем, а только для статистической связи линейного типа. Эта связь характерна тем, что при усилении этой связи растет
максимален. Далее будет показано, что это предположение верно, но не в общем, а только для статистической связи линейного типа. Эта связь характерна тем, что при усилении этой связи растет ![]() , и в пределе связь вырождается в линейную зависимость (56.1).
, и в пределе связь вырождается в линейную зависимость (56.1).
Однако если связь имеет нелинейный характер, то величина ![]() не отражает меру (степень) этой связи. Рассмотрим следующий пример. Пусть
не отражает меру (степень) этой связи. Рассмотрим следующий пример. Пусть ![]() ,
, ![]() , и
, и ![]() - случайная величина с равномерным на интервале
- случайная величина с равномерным на интервале ![]() распределением вероятностей. Случайные величины
распределением вероятностей. Случайные величины ![]() и
и ![]() связаны между собой соотношением:
связаны между собой соотношением: ![]() . Таким образом, между величинами
. Таким образом, между величинами ![]() и
и ![]() существует функциональная связь, а не статистическая, и следовало ожидать, что величина
существует функциональная связь, а не статистическая, и следовало ожидать, что величина ![]() максимальна. Однако, прямые вычисления приводят к результату
максимальна. Однако, прямые вычисления приводят к результату ![]() . Действительно,
. Действительно,
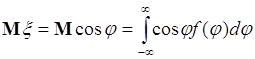 , (56.6)
, (56.6)
где

- плотность распределения вероятностей случайной величины ![]() . С учетом этого (56.6) преобразуется:
. С учетом этого (56.6) преобразуется:
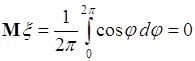 .
.
Аналогично
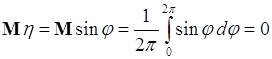 ,
,
теперь ковариация
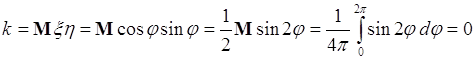 .
.
Таким образом, для нелинейной связи между случайными величинами их ковариация не может использоваться как мера статистической связи, поскольку значение ковариации не отражает степень этой связи.
Ковариация и геометрия линий равного уровня плотности вероятности
Ковариация случайных величин ![]() и
и ![]() определяется через их совместную плотность вероятности
определяется через их совместную плотность вероятности ![]() соотношением:
соотношением:
 . (57.1)
. (57.1)
Подынтегральная функция в (57.1) неотрицательна для таких ![]() ,
, ![]() , при которых
, при которых ![]() , то есть при
, то есть при ![]() ,
, ![]() или
или ![]() ,
, ![]() . И наоборот, при
. И наоборот, при ![]() ,
, ![]() или
или ![]() ,
, ![]() подынтегральная функция (57.1) отрицательна либо равна нулю. Знак ковариации зависит от того, какие значения, положительные или отрицательные преобладают в подынтегральной функции. Поэтому знак числа
подынтегральная функция (57.1) отрицательна либо равна нулю. Знак ковариации зависит от того, какие значения, положительные или отрицательные преобладают в подынтегральной функции. Поэтому знак числа ![]() определяется расположением линий равного уровня плотности вероятности
определяется расположением линий равного уровня плотности вероятности ![]() . На рис. 57.1 представлен пример линий равного уровня функции
. На рис. 57.1 представлен пример линий равного уровня функции ![]() , для которой
, для которой ![]() . Штриховкой
. Штриховкой
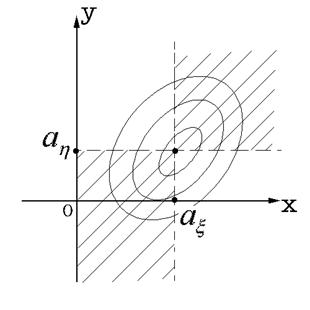
Рис. 57.1.
Линии равного уровня плотности вероятности при ![]() .указана часть плоскости, на которой
.указана часть плоскости, на которой ![]() , и следовательно неотрицательна подынтегральная функция. Поскольку в заштрихованной области (положительные значения подынтегральной функции) плотность
, и следовательно неотрицательна подынтегральная функция. Поскольку в заштрихованной области (положительные значения подынтегральной функции) плотность ![]() имеет в среднем большее значение, чем в нештрихованной области (отрицательные значения подынтегральной функции), то ковариация
имеет в среднем большее значение, чем в нештрихованной области (отрицательные значения подынтегральной функции), то ковариация ![]() . На рис. 57.2 представлены линии равного уровня плотности
. На рис. 57.2 представлены линии равного уровня плотности ![]() при
при ![]() . Случай
. Случай ![]() соответствует симметричному расположению линий относительно прямой
соответствует симметричному расположению линий относительно прямой ![]() (или
(или ![]() ). Например, эти линии могут быть эллипсами, у которых большая полуось совпадает по направлению с прямой
). Например, эти линии могут быть эллипсами, у которых большая полуось совпадает по направлению с прямой ![]() (или
(или ![]() ). Другой пример – линии являются окружностями с центром в точке
). Другой пример – линии являются окружностями с центром в точке ![]() .
.
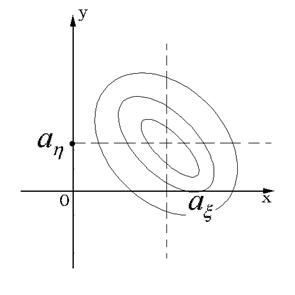
Рис. 57.2. Линии равного уровня плотности
вероятности при ![]() .
.
Отметим, что если ![]() , а линии равного уровня имеют ось симметрии, например, на рис. 57.1 линии – это эллипсы, тогда можно выполнить преобразование (вращение) системы координат
, а линии равного уровня имеют ось симметрии, например, на рис. 57.1 линии – это эллипсы, тогда можно выполнить преобразование (вращение) системы координат ![]() , такое, что в новой системе ковариация
, такое, что в новой системе ковариация ![]() . Это означает также и преобразование случайных величин
. Это означает также и преобразование случайных величин ![]() ,
, ![]() с ненулевой ковариацией к новым случайным величинам, для которых ковариация равна нулю.
с ненулевой ковариацией к новым случайным величинам, для которых ковариация равна нулю.
Коэффициент корреляции
58.1. Коэффициентом корреляции двух случайных величин ![]() и
и ![]() называется число
называется число
 . (58.1)
. (58.1)
Коэффициент корреляции является ковариацией: ![]() двух безразмерных случайных величин
двух безразмерных случайных величин
 ,
,  , (58.2)
, (58.2)
полученных из исходных величин ![]() и
и ![]() путем преобразования специального вида (58.2) (нормировки), которое обеспечивает нулевые средние
путем преобразования специального вида (58.2) (нормировки), которое обеспечивает нулевые средние ![]() ,
, ![]() и единичные дисперсии
и единичные дисперсии ![]() ,
, ![]() .
.
Коэффициент корреляции (58.1) можно представить через ковариацию ![]() случайных величин
случайных величин ![]() и
и ![]() :
:
 . (58.3)
. (58.3)
Поскольку ![]() , то из (58.3) следует
, то из (58.3) следует
![]() . (58.4)
. (58.4)
Коэффициент корреляции является безразмерной величиной, принимает значения на интервале ![]() и поэтому используется как мера статистической связи линейного типа между случайными величинами
и поэтому используется как мера статистической связи линейного типа между случайными величинами ![]() и
и ![]() , в отличие от ковариации
, в отличие от ковариации ![]() , для которой интервал значений
, для которой интервал значений ![]() зависит от дисперсий случайных величин. Рассмотрим примеры вычисления коэффициента корреляции, позволяющие выяснить свойства
зависит от дисперсий случайных величин. Рассмотрим примеры вычисления коэффициента корреляции, позволяющие выяснить свойства ![]() как меры статистической связи между случайными величинами.
как меры статистической связи между случайными величинами.
58.2. Пусть ![]() - случайная величина с математическим ожиданием
- случайная величина с математическим ожиданием ![]() , дисперсией
, дисперсией ![]() и
и ![]() . Ковариация случайных величин
. Ковариация случайных величин ![]() и
и ![]() определяется формулой (56.5):
определяется формулой (56.5): ![]() . Подставим это соотношение в (58.3) , тогда:
. Подставим это соотношение в (58.3) , тогда:
 (58.4)
(58.4)
Таким образом, для случайных величин ![]() ,
, ![]() , связанных линейной зависимостью коэффициент корреляции
, связанных линейной зависимостью коэффициент корреляции ![]() принимает либо максимальное значение
принимает либо максимальное значение ![]() , либо минимальное -
, либо минимальное - ![]() .
.
58.3. Рассмотрим обобщение линейной функции, связывающей случайные величины ![]() и
и ![]() на линейную случайную функцию следующего вида:
на линейную случайную функцию следующего вида:
![]() (58.5)
(58.5)
где ![]() и
и ![]() - независимые случайные величины. В частном случае
- независимые случайные величины. В частном случае ![]() - число и (58.5) – линейная функция, определяющая
- число и (58.5) – линейная функция, определяющая ![]() через
через ![]() . Для детерминированной линейной связи
. Для детерминированной линейной связи ![]() - принимает максимальное значение. Если
- принимает максимальное значение. Если ![]() - случайная величина, то связь (58.5) становится статистической (стохастической, случайной), то есть не столь жесткой как детерминированная функциональная связь. Это приводит к
- случайная величина, то связь (58.5) становится статистической (стохастической, случайной), то есть не столь жесткой как детерминированная функциональная связь. Это приводит к ![]() . В зависимости от свойств случайной величины
. В зависимости от свойств случайной величины ![]() статистическая связь между
статистическая связь между ![]() и
и ![]() может быть сильной,
может быть сильной, ![]() , или слабой,
, или слабой, ![]() . Для того, чтобы ответить на вопрос, какова мера связи между случайными величинами
. Для того, чтобы ответить на вопрос, какова мера связи между случайными величинами ![]() и
и ![]() (58.5) вычислим их коэффициент корреляции.
(58.5) вычислим их коэффициент корреляции.
Пусть ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Тогда из (58.5) следует, в силу независимости
. Тогда из (58.5) следует, в силу независимости ![]() и
и![]() :
:
![]() .
.
Выразим дисперсию случайные величины ![]() через параметры случайных величин
через параметры случайных величин ![]() ,
,![]() :
:
![]() . (58.6)
. (58.6)
Теперь по формуле (58.3):
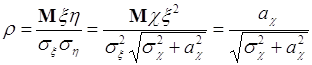 . (58.7)
. (58.7)
Если ![]() , то из (58.7) следует
, то из (58.7) следует ![]() , что соответствует слабой связи между случайными величинами
, что соответствует слабой связи между случайными величинами ![]() и
и ![]() . Если
. Если ![]() , из (58.7) следует
, из (58.7) следует ![]() , связь становится сильной и в пределе при
, связь становится сильной и в пределе при ![]() переходит в детерминированную линейную связь.
переходит в детерминированную линейную связь.
Коэффициент корреляции и расстояние
59.1. Пусть ![]() - множество элементов
- множество элементов ![]() Расстоянием (метрикой) между элементами
Расстоянием (метрикой) между элементами ![]() множества
множества ![]() называется неотрицательная функция
называется неотрицательная функция ![]() , удовлетворяющая следующим трем аксиомам:
, удовлетворяющая следующим трем аксиомам:
![]() , причем
, причем ![]() .
.
![]() .
.
![]() .
.
Вторая аксиома называется условием симметрии, а третья – неравенством треугольника. Если аксиому 1 ослабить: ![]() , тогда
, тогда ![]() называется псевдометрикой. Для псевдометрики из условия
называется псевдометрикой. Для псевдометрики из условия ![]() не обязательно следует
не обязательно следует ![]() .
.
Пусть ![]() - множество случайных величин. Для каждой пары
- множество случайных величин. Для каждой пары ![]() элементов этого множества можно также ввести расстояние
элементов этого множества можно также ввести расстояние ![]() вида
вида
![]() . (59.1)
. (59.1)
Покажем, что функция ![]() является псевдометрикой. Аксиома 1 – очевидна:
является псевдометрикой. Аксиома 1 – очевидна: ![]() , причем из условия
, причем из условия ![]() следует
следует ![]() . Аксиома 2 также очевидна. Рассмотрим аксиому 3. Справедливы следующие преобразования:
. Аксиома 2 также очевидна. Рассмотрим аксиому 3. Справедливы следующие преобразования:
![]()
(59.2)
Пусть ![]() - корреляция двух случайных величин
- корреляция двух случайных величин ![]() и
и ![]() . Известно, что
. Известно, что ![]() удовлетворяет неравенству (55.2)
удовлетворяет неравенству (55.2)
![]() . (59.3)
. (59.3)
Подставим (59.3) в (59.2), тогда
![]()
![]() , (59.4)
, (59.4)
что и доказывает третью аксиому.
Похожие работы
... математического ожидания. Таким образом, (72.6) принимает вид . (72.7) 72.2. Функции вида , (72.8) где целые числа , называются начальными моментами порядка случайного процесса . Аналогично центральные моменты определяются соотношениями: . (72.9) Для функций (72.8), (72.9) используется общее название - моментные функции. Наиболее простые ...
... damn(t)/dt =[daij(t)/dt] 1.3 ПОНЯТИЕ ДИНАМЧЕСКОГО ОБЬЕКТА. Физический объект - физическое устройство, характеризуемое некоторым числом свойств, соответствующих целям его использования. В теории систем существенным является не физическое, а математическое описание свойств объекта и соотношений между ними. В теории систем объектом А является абстрактный объект, связанный с множеством ...
... проверить знания студента из первой части курса, которая излагается в первых четырёх модулях. Во вторых вопросах билета проверяются знания классической предельной проблемы теории вероятностей и математической статистики, которые излагаются в следующих пяти модулях. 1. Вероятностная модель с не более чем счётным числом элементарных исходов. Пример: испытания с равновозможными исходами. 2. ...
... несколько уравнений, а в каждом уравнении - несколько переменных. Задача оценивания параметров такой разветвленной модели решается с помощью сложных и причудливых методов. Однако все они имеют одну и ту же теоретическую основу. Поэтому для получения начального представления о содержании эконометрических методов мы ограничимся в последующих параграфах рассмотрением простой линейной регрессии. ...
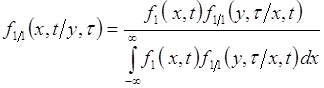




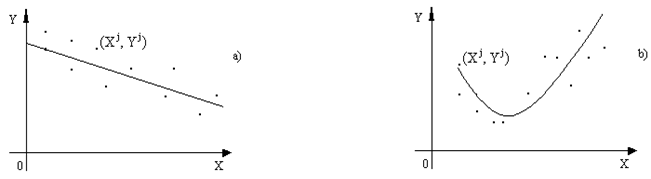
0 комментариев