Навигация
Случайные вектора
Оглавление
Функция распределения вероятностей двух случайных величин.. 2
Совместная плотность распределения вероятности двух случайных величин 4
Условная функция распределения вероятностей.. 7
Условная плотность вероятности.. 7
Числовые характеристики двумерного случайного вектора. 8
Верхняя и нижняя границы корреляции и ковариации.. 10
Ковариация и независимость двух случайных величин.. 11
Ковариация и геометрия линий равного уровня плотности вероятности 13
Коэффициент корреляции.. 15
Коэффициент корреляции и расстояние. 17
Функция распределения вероятностей случайного вектора. 18
Плотность вероятности случайного вектора. 19
Многомерное нормальное распределение. 21
Характеристическая функция случайного вектора. 22
Функции от случайных величин.. 23
Распределение вероятностей функции одной случайной величины.. 24
Преобразование нескольких случайных величин.. 28
Хи - квадрат распределение вероятностей.. 30
Хи - квадрат распределение и распределение Максвелла по скоростям.. 33
Литература. 35
Функция распределения вероятностей двух случайных величин
В задачах со случайным исходом обычно приходится учитывать взаимодействие нескольких случайных величин. Это естественным образом приводит к понятию многомерных (векторных) случайных величин или совокупности нескольких случайных величин. Случайный вектор является третьим основным объектом изучения теории вероятностей (после случайного события и случайной величины). Целесообразно начать изучение случайных векторов с рассмотрения двухмерных векторов, свойства которых сравнительно простые и наглядные.
Совместной функцией распределения вероятностей (или двумерной функцией распределения вероятностей) случайных величин ![]() ,
, ![]() (или случайного вектора
(или случайного вектора ![]() ) называется функция
) называется функция
![]() . (50.1)
. (50.1)
Следует иметь в виду, что ![]() - вероятность события
- вероятность события ![]() - пересечения двух событий:
- пересечения двух событий: ![]() и
и ![]() . В записях вида (50.1) принято вместо символа
. В записях вида (50.1) принято вместо символа ![]() использовать запятую.
использовать запятую.
50.1. Рассмотрим основные свойства функции ![]() , следующие из ее определения.
, следующие из ее определения.
1). ![]() , где
, где ![]() - функция распределения вероятностей случайной величины
- функция распределения вероятностей случайной величины ![]() . Действительно,
. Действительно, ![]() - достоверное событие, поэтому
- достоверное событие, поэтому ![]() . Аналогично
. Аналогично ![]() , где
, где ![]() - функция распределения вероятностей случайной величины
- функция распределения вероятностей случайной величины ![]() .
.
2). ![]() , поскольку события
, поскольку события ![]() ,
, ![]() - достоверные, следовательно их пересечение – достоверное событие и
- достоверные, следовательно их пересечение – достоверное событие и ![]() .
.
3). ![]() , поскольку событие
, поскольку событие ![]() - невозможное и
- невозможное и ![]() . Аналогично
. Аналогично ![]() .
.
4). ![]() - неубывающая функция аргумента
- неубывающая функция аргумента ![]() , а также неубывающая функция аргумента
, а также неубывающая функция аргумента ![]() .
.
5). ![]() непрерывна справа по каждому аргументу.
непрерывна справа по каждому аргументу.
50.2. Рассмотрим геометрическую интерпретацию функции ![]() . Пусть случайные величины
. Пусть случайные величины ![]() ,
, ![]() являются компонентами случайного вектора
являются компонентами случайного вектора ![]() . Тогда результат каждого опыта по измерению случайного вектора
. Тогда результат каждого опыта по измерению случайного вектора ![]() можно рассматривать как точку на плоскости, а функция
можно рассматривать как точку на плоскости, а функция ![]() определяет вероятность попадания точки в часть плоскости:
определяет вероятность попадания точки в часть плоскости: ![]() , выделенной на рис. 50.1 штриховкой.
, выделенной на рис. 50.1 штриховкой.
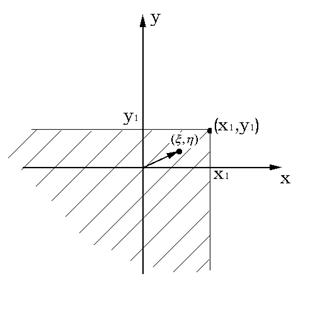
Рис. 50.1. Геометрическая интерпретация функции ![]() .
.
Представим вероятность ![]() - попадания случайного вектора
- попадания случайного вектора ![]() в прямоугольник
в прямоугольник ![]() ,
, ![]() ,
, ![]() ,
, ![]() , рис 50.2, через функцию
, рис 50.2, через функцию ![]() . Несложно определить, что
. Несложно определить, что
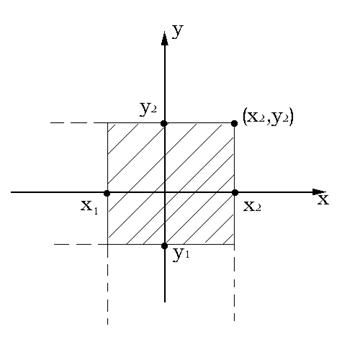
Рис. 50.2. К вычислению вероятности попадания в прямоугольник.
![]()
(50.2)
Пусть ![]() ,
, ![]() - малые величины и функция
- малые величины и функция ![]() имеет первые производные по
имеет первые производные по ![]() и
и ![]() , а также вторую смешанную производную, тогда из (50.2) следует:
, а также вторую смешанную производную, тогда из (50.2) следует:
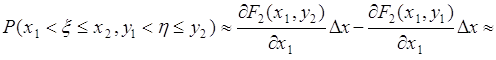
 . (50.3)
. (50.3)
Отсюда:
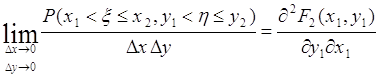 . (50.4)
. (50.4)
Пусть у функции ![]() существуют производные по
существуют производные по ![]() ,
, ![]() , а также вторая смешанная производная. Совместной (или двумерной) плотностью распределения вероятностей случайных величин
, а также вторая смешанная производная. Совместной (или двумерной) плотностью распределения вероятностей случайных величин ![]() и
и ![]() называется функция
называется функция
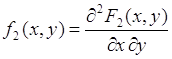 (51.1)
(51.1)
Рассмотрим основные свойства двумерной плотности вероятности.
1. Справедливо соотношение:
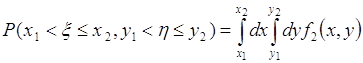 . (51.2)
. (51.2)
Для доказательства используем равенство (51.1), тогда:
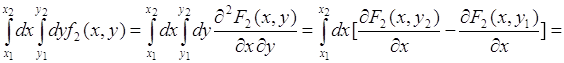
![]() . (51.3)
. (51.3)
Теперь из равенства (50.2) следует (51.2). Это соотношение имеет практическое значение, поскольку позволяет вычислять вероятность ![]() - попадания двумерного вектора
- попадания двумерного вектора ![]() в прямоугольник, определяемый отрезками
в прямоугольник, определяемый отрезками ![]() и
и ![]() через плотность вероятности
через плотность вероятности ![]() .
.
2. Рассмотрим частный случай соотношения (51.2). Пусть ![]() ,
, ![]() ,
, ![]() ,
, ![]() , тогда (51.2) принимает вид:
, тогда (51.2) принимает вид:
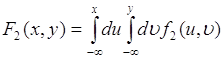 . (51.4)
. (51.4)
Это соотношение определяет функцию распределения вероятностей ![]() через плотность вероятности
через плотность вероятности ![]() и является обратным по отношению к равенству (51.1).
и является обратным по отношению к равенству (51.1).
3. Рассмотрим (51.2) при условиях: ![]() ,
, ![]() ,
, ![]() ,
, ![]() , тогда из (51.2) следует равенство:
, тогда из (51.2) следует равенство:
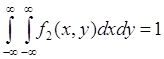 , (51.5)
, (51.5)
поскольку ![]() - как вероятность достоверного события. Соотношение (51.5) называется условием нормировки для плотности вероятности
- как вероятность достоверного события. Соотношение (51.5) называется условием нормировки для плотности вероятности ![]() .
.
4. Если ![]() - плотность вероятности вектора
- плотность вероятности вектора ![]() , и
, и ![]() - плотность вероятности случайной величины
- плотность вероятности случайной величины ![]() , то
, то
 . (51.6)
. (51.6)
Это равенство называется свойством согласованности плотности второго порядка ![]() и плотности первого порядка
и плотности первого порядка ![]() . Если известна плотность второго порядка
. Если известна плотность второго порядка ![]() , то по формуле (51.6) можно вычислить плотность вероятности
, то по формуле (51.6) можно вычислить плотность вероятности ![]() - случайной величины
- случайной величины ![]() . Аналогично,
. Аналогично,
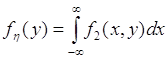 . (51.7)
. (51.7)
Доказательство (51.6) получим на основе равенства
![]() . (51.8)
. (51.8)
Представим ![]() через плотность
через плотность ![]() согласно (51.4), а
согласно (51.4), а ![]() через
через ![]() , тогда из (51.8) следует
, тогда из (51.8) следует
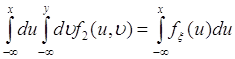 . (51.9)
. (51.9)
Дифференцирование (51.9) по ![]() приводит к равенству (51.6), что и завершает доказательство.
приводит к равенству (51.6), что и завершает доказательство.
5. Случайные величины ![]() и
и ![]() называются независимыми, если независимы случайные события
называются независимыми, если независимы случайные события ![]() и
и ![]() при любых числах
при любых числах ![]() и
и ![]() . Для независимых случайных величин
. Для независимых случайных величин ![]() и
и ![]() :
:
![]() . (51.10)
. (51.10)
Доказательство следует из определений функций ![]() и
и ![]() ,
, ![]() . Поскольку
. Поскольку ![]() и
и ![]() - независимые случайные величины, то события вида:
- независимые случайные величины, то события вида: ![]() и
и ![]() - независимые для любых
- независимые для любых ![]() и
и ![]() . Поэтому
. Поэтому
![]() (51.11)
(51.11)
- справедливо равенство (51.10). Продифференцируем (51.10) по ![]() и
и ![]() , тогда согласно (51.1) получаем следствие для плотностей:
, тогда согласно (51.1) получаем следствие для плотностей:
![]() . (51.12)
. (51.12)
6. Пусть ![]() - произвольная область на плоскости
- произвольная область на плоскости ![]() , тогда
, тогда
![]() (51.13)
(51.13)
- вероятность того, что вектор ![]() принимает любые значения из области
принимает любые значения из области ![]() определяется интегралом по
определяется интегралом по ![]() от плотности вероятности
от плотности вероятности ![]() .
.
Рассмотрим пример случайного вектора ![]() с равномерным распределением вероятностей, который имеет плотность вероятности
с равномерным распределением вероятностей, который имеет плотность вероятности ![]() на прямоугольнике
на прямоугольнике ![]() и
и ![]() - вне этого прямоугольника. Число
- вне этого прямоугольника. Число![]() определяется из условия нормировки:
определяется из условия нормировки:
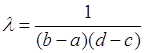 .
.
Пусть случайные величины ![]() и
и ![]() имеют плотности вероятности
имеют плотности вероятности ![]() и
и ![]() соответственно и совместную плотность
соответственно и совместную плотность ![]() . Рассмотрим равенство:
. Рассмотрим равенство:
![]() . (52.1)
. (52.1)
Отсюда
 (52.2)
(52.2)
Функция
![]() (52.3)
(52.3)
называется условной функцией распределения вероятностей случайной величины ![]() при условии, что случайная величина
при условии, что случайная величина ![]() принимает значение
принимает значение ![]()
![]() .
.
Подставим (52.2) в (52.3), тогда
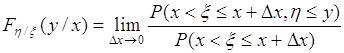 . (52.4)
. (52.4)
Представим вероятности в (52.4) через плотности вероятностей, тогда
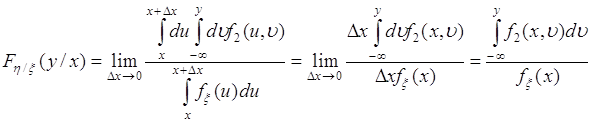 (52.5)
(52.5)
Это соотношение определяет условную функцию ![]() через плотности
через плотности ![]() и
и ![]() . Отметим, что для независимых случайных величин
. Отметим, что для независимых случайных величин ![]() и
и ![]() совместная плотность
совместная плотность ![]() . При этом, как следует из (52.5), условная функция
. При этом, как следует из (52.5), условная функция ![]() - не зависит от аргумента
- не зависит от аргумента ![]() (т.е. не зависит от событий вида
(т.е. не зависит от событий вида ![]() .
.
Аналогично (52.3) можно определить функцию ![]() случайной величины
случайной величины ![]() при условии, что
при условии, что ![]() , и затем получить выражение аналогичное (52.5)
, и затем получить выражение аналогичное (52.5)
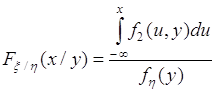 . (52.6)
. (52.6)
Условной плотностью распределения вероятностей случайной величины ![]() при условии
при условии ![]() называется функция:
называется функция:
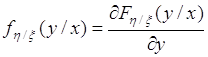 . (53.1)
. (53.1)
Соотношение (52.5) подставим в (53.1), тогда
 . (53.2)
. (53.2)
Отсюда следует
![]() . (53.3)
. (53.3)
- формула умножения для плотностей. Эта формула аналогична формуле умножения вероятностей. Очевидно,
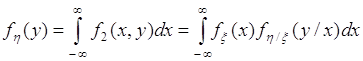 . (53.4)
. (53.4)
Данное равенство является аналогом формулы полной вероятности.
Аналогично (53.1) вводится условная плотность распределения вероятности случайной величины ![]() при условии
при условии ![]() как функция вида:
как функция вида:
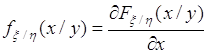 . (53.5)
. (53.5)
Отсюда и из (52.6) следуют соотношения:
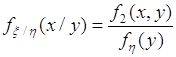 , (53.6)
, (53.6)
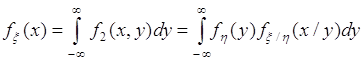 . (53.7)
. (53.7)
В (53.6) подставим (53.3) и (53.4), тогда:
 . (53.8)
. (53.8)
Это соотношение аналогично формуле Байеса. Здесь случайные величины ![]() и
и ![]() можно поменять местами, тогда получим также верное соотношение для условной плотности
можно поменять местами, тогда получим также верное соотношение для условной плотности ![]() , которая определяется через функции
, которая определяется через функции ![]() и
и ![]() .
.
54.1. Пусть случайные величины ![]() и
и ![]() имеют совместную плотность вероятности
имеют совместную плотность вероятности ![]() и
и ![]() - функция двух переменных. Тогда
- функция двух переменных. Тогда ![]() - случайная величина, полученная подстановкой случайных величин
- случайная величина, полученная подстановкой случайных величин ![]() и
и ![]() вместо аргументов
вместо аргументов ![]() и
и ![]() .
.
Математическим ожиданием случайной величины ![]() называется число
называется число
 . (54.1)
. (54.1)
Если ![]() ,
, ![]() , тогда из (54.1) следует
, тогда из (54.1) следует
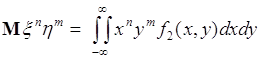 ,
, ![]() ,
, ![]() . (54.2)
. (54.2)
Числа ![]() называются начальными смешанными моментами порядка
называются начальными смешанными моментами порядка ![]() случайных величин
случайных величин ![]() и
и ![]() . Эти числа применяются в качестве статистических характеристик двумерного случайного вектора. Рассмотрим частные случаи (54.2). 1).
. Эти числа применяются в качестве статистических характеристик двумерного случайного вектора. Рассмотрим частные случаи (54.2). 1). ![]() , тогда
, тогда ![]() - начальный момент порядка
- начальный момент порядка ![]() случайной величины
случайной величины ![]() . При дополнительном условии
. При дополнительном условии ![]() получаем
получаем ![]() - математическое ожидание случайной величины
- математическое ожидание случайной величины ![]() , при
, при ![]() -
- ![]() - среднее ее квадрата и т.д. Таким образом, при
- среднее ее квадрата и т.д. Таким образом, при ![]() смешанные моменты (54.2) совпадают с начальными моментами случайной величины
смешанные моменты (54.2) совпадают с начальными моментами случайной величины ![]() . 2). Если положить
. 2). Если положить ![]() , тогда
, тогда ![]() - смешанные моменты совпадают с начальными моментами случайной величины
- смешанные моменты совпадают с начальными моментами случайной величины ![]() . В обоих случаях получаем индивидуальные характеристики одной из случайных величин. 3). Для получения групповой характеристики (54.2), отражающей свойства совокупности двух случайных величин, необходимо рассмотреть ненулевые
. В обоих случаях получаем индивидуальные характеристики одной из случайных величин. 3). Для получения групповой характеристики (54.2), отражающей свойства совокупности двух случайных величин, необходимо рассмотреть ненулевые ![]() . Наиболее простой вариант:
. Наиболее простой вариант: ![]() ,
, ![]() . При этом из (54.2) следует
. При этом из (54.2) следует
 . (54.3)
. (54.3)
Число ![]() называется корреляцией случайных величин
называется корреляцией случайных величин ![]() и
и ![]() и представляет собой важнейшую характеристику совокупности двух случайных величин.
и представляет собой важнейшую характеристику совокупности двух случайных величин.
Если ![]() и
и ![]() - независимы, то
- независимы, то ![]() и (54.3) преобразуются следующим образом:
и (54.3) преобразуются следующим образом:
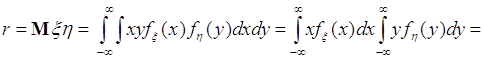
![]() , (54.4)
, (54.4)
где ![]() и
и ![]() . При этом
. При этом ![]() выражается через индивидуальные характеристики
выражается через индивидуальные характеристики ![]() и
и ![]() , т.е. каких-либо групповых эффектов в
, т.е. каких-либо групповых эффектов в ![]() не проявляется, что является следствием независимости случайных величин
не проявляется, что является следствием независимости случайных величин ![]() и
и ![]() . Из цепочки преобразований (54.4) следует равенство
. Из цепочки преобразований (54.4) следует равенство ![]() - математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий.
- математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий.
Похожие работы
... математического ожидания. Таким образом, (72.6) принимает вид . (72.7) 72.2. Функции вида , (72.8) где целые числа , называются начальными моментами порядка случайного процесса . Аналогично центральные моменты определяются соотношениями: . (72.9) Для функций (72.8), (72.9) используется общее название - моментные функции. Наиболее простые ...
... damn(t)/dt =[daij(t)/dt] 1.3 ПОНЯТИЕ ДИНАМЧЕСКОГО ОБЬЕКТА. Физический объект - физическое устройство, характеризуемое некоторым числом свойств, соответствующих целям его использования. В теории систем существенным является не физическое, а математическое описание свойств объекта и соотношений между ними. В теории систем объектом А является абстрактный объект, связанный с множеством ...
... проверить знания студента из первой части курса, которая излагается в первых четырёх модулях. Во вторых вопросах билета проверяются знания классической предельной проблемы теории вероятностей и математической статистики, которые излагаются в следующих пяти модулях. 1. Вероятностная модель с не более чем счётным числом элементарных исходов. Пример: испытания с равновозможными исходами. 2. ...
... несколько уравнений, а в каждом уравнении - несколько переменных. Задача оценивания параметров такой разветвленной модели решается с помощью сложных и причудливых методов. Однако все они имеют одну и ту же теоретическую основу. Поэтому для получения начального представления о содержании эконометрических методов мы ограничимся в последующих параграфах рассмотрением простой линейной регрессии. ...
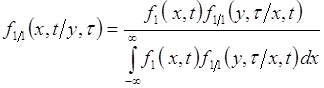




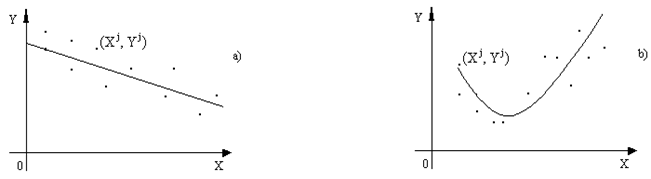
0 комментариев