Навигация
СЛУЧАЙНЫЕ ПРОЦЕССЫ
Оглавление
Случайная функция, случайный процесс, случайное поле. 2
Функция распределения вероятностей случайного процесса. 3
Плотность распределения вероятностей случайного процесса. 4
Моментные функции случайного процесса. 5
Условные распределения вероятностей. 6
Примеры математических моделей случайных процессов. 7
Стационарные процессы.. 8
Литература. 10
Случайная функция, случайный процесс, случайное поле
69.1. Случайной функцией ![]() называется случайная величина
называется случайная величина ![]() , зависимая от параметра
, зависимая от параметра ![]() . Случайные величины
. Случайные величины ![]() могут быть вещественными, либо комплексными, либо векторными; аргумент
могут быть вещественными, либо комплексными, либо векторными; аргумент ![]() может быть вещественным или векторным. Самый простой пример случайной функции получаем для вещественного параметра
может быть вещественным или векторным. Самый простой пример случайной функции получаем для вещественного параметра ![]() и вещественной случайной величины
и вещественной случайной величины ![]() . При этом
. При этом ![]() называется случайной функцией одной переменной или случайным процессом. Отметим, что аргумент
называется случайной функцией одной переменной или случайным процессом. Отметим, что аргумент ![]() случайного процесса не обязательно имеет размерность времени.
случайного процесса не обязательно имеет размерность времени.
Более сложные примеры случайных функций встречаются в задачах физики, океанологии, метеорологии и других областях приложения теории вероятностей. Так, температура воздуха ![]() в точке пространства
в точке пространства ![]() и в момент времени
и в момент времени ![]() часто рассматривается как случайная величина. Таким образом, температура воздуха
часто рассматривается как случайная величина. Таким образом, температура воздуха ![]() является случайной функцией, зависимой от трех декартовых координат
является случайной функцией, зависимой от трех декартовых координат ![]() времени
времени ![]() . Случайную функцию, зависимую от нескольких переменных принято называть случайным полем.
. Случайную функцию, зависимую от нескольких переменных принято называть случайным полем.
69.2. Случайный процесс ![]() как функция аргумента
как функция аргумента ![]() имеет свою область определения
имеет свою область определения ![]() , которая может быть отрезком на вещественной оси, положительной полуосью, всей вещественной осью и т. д. Рассмотрим случайный процесс
, которая может быть отрезком на вещественной оси, положительной полуосью, всей вещественной осью и т. д. Рассмотрим случайный процесс ![]() при фиксированном
при фиксированном ![]() , тогда
, тогда ![]() - случайная величина, которая называется сечением случайного процесса в точке
- случайная величина, которая называется сечением случайного процесса в точке ![]() .
.
Пусть выполняется ![]() опытов, в каждом из которых измеряется значение
опытов, в каждом из которых измеряется значение ![]() ,
, ![]() , случайной величины
, случайной величины ![]() . Тогда результаты измерений – это
. Тогда результаты измерений – это ![]() чисел
чисел
![]() . (69.1)
. (69.1)
В отличие от случайной величины ![]() измерение случайного процесса
измерение случайного процесса ![]() выполняется в течение некоторого интервала
выполняется в течение некоторого интервала ![]() -интервала наблюдения. Последний либо содержится в области определения
-интервала наблюдения. Последний либо содержится в области определения ![]() , либо совпадает с ней. Пусть детерминированная функция
, либо совпадает с ней. Пусть детерминированная функция ![]() ,
, ![]() , - результат измерения случайного процесса в первом опыте, функция
, - результат измерения случайного процесса в первом опыте, функция ![]() ,
, ![]() , - результат измерения случайного процесса во втором опыте, и т.д. Тогда результаты всех
, - результат измерения случайного процесса во втором опыте, и т.д. Тогда результаты всех ![]() опытов, аналогично (69.1), представляются совокупностью
опытов, аналогично (69.1), представляются совокупностью ![]() детерминированных функций времени:
детерминированных функций времени:
![]() (69.2)
(69.2)
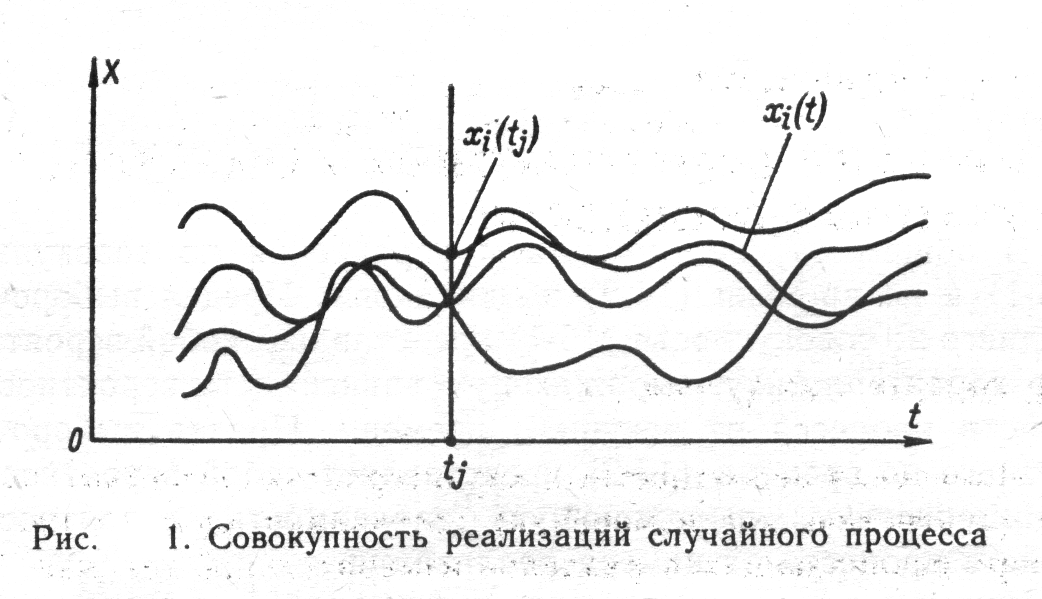
Каждая функция ![]() ,
, ![]() , называется реализацией (траекторией, выборочной функцией, выборкой) случайного процесса
, называется реализацией (траекторией, выборочной функцией, выборкой) случайного процесса ![]() . Совокупность (69.2) называется ансамблем реализаций случайного процесса
. Совокупность (69.2) называется ансамблем реализаций случайного процесса ![]() . Ансамбль реализаций содержит информацию о статистических свойствах случайного процесса
. Ансамбль реализаций содержит информацию о статистических свойствах случайного процесса ![]() аналогично как и совокупность измерений (69.1) содержит информацию о статистических свойствах случайной величины
аналогично как и совокупность измерений (69.1) содержит информацию о статистических свойствах случайной величины ![]() .
.
69.3. В зависимости от того, дискретны или непрерывны время ![]() и реализации
и реализации ![]() ,
различают четыре типа случайных процессов.
,
различают четыре типа случайных процессов.
1). Случайный процесс общего типа: время ![]() - непрерывно и реализации
- непрерывно и реализации ![]() - непрерывны.
- непрерывны.
2). Дискретный случайный процесс: время ![]() - непрерывно и
- непрерывно и ![]() - дискретны.
- дискретны.
3). Случайная последовательность: ![]() - дискретно и
- дискретно и ![]() - непрерывны. В литературе случайные процессы этого типа принято называть временными рядами.
- непрерывны. В литературе случайные процессы этого типа принято называть временными рядами.
4). Дискретная случайная последовательность: ![]() - дискретно и
- дискретно и ![]() - дискретны.
- дискретны.
70.1. При фиксированном ![]() распределение вероятностей сечения
распределение вероятностей сечения ![]() случайного процесса (как распределение вероятностей случайной величины) задается функцией распределения вероятностей
случайного процесса (как распределение вероятностей случайной величины) задается функцией распределения вероятностей
![]() . (70.1)
. (70.1)
Соотношение (70.1) можно рассматривать при любом ![]() . Функция
. Функция ![]() , как функция двух переменных
, как функция двух переменных ![]() и
и ![]() , называется одномерной функцией распределения вероятностей случайного процесса
, называется одномерной функцией распределения вероятностей случайного процесса ![]() . Аргументы
. Аргументы ![]() и
и ![]() принято называть соответственно фазовой и временной переменными. Однако,
принято называть соответственно фазовой и временной переменными. Однако, ![]() не дает исчерпывающую вероятностную характеристику случайного процесса
не дает исчерпывающую вероятностную характеристику случайного процесса ![]() , поскольку она не учитывает зависимости случайных величин
, поскольку она не учитывает зависимости случайных величин ![]() при разных
при разных ![]() (т.е. зависимости разных сечений случайного процесса). Более полно вероятностные свойства случайного процесса
(т.е. зависимости разных сечений случайного процесса). Более полно вероятностные свойства случайного процесса ![]() описывает
описывает ![]() -мерная функция распределения
-мерная функция распределения ![]() - функция распределения случайного вектора
- функция распределения случайного вектора ![]() :
:
![]() . (70.2)
. (70.2)
Однако, практическое применение находят лишь функции распределения первого и второго порядков ![]() . Функции более высоких порядков
. Функции более высоких порядков ![]() используются только в теории.
используются только в теории.
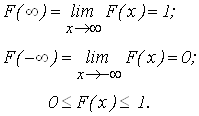
70.2. Основные свойства ![]() -мерной функции распределения вероятностей случайного процесса аналогичны свойствам функции распределения вероятностей
-мерной функции распределения вероятностей случайного процесса аналогичны свойствам функции распределения вероятностей ![]() -мерного вектора.
-мерного вектора.
1) Функция ![]() - неубывающая по каждому аргументу
- неубывающая по каждому аргументу ![]() ,
, ![]() .
.
2) Функция ![]() - непрерывна справа по каждому аргументу
- непрерывна справа по каждому аргументу ![]() ,
, ![]() .
.
3) Функция распределения симметрична относительно перестановок двух любых пар ![]() и
и ![]() :
:
![]() .
.
4) Для любого целого ![]() ,
,
![]()
![]() .
.
5) Для любого целого ![]() ,
,
![]()
![]() .
.
6) ![]() .
.
Если ![]() имеет производную
имеет производную
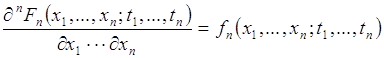 , (71.1)
, (71.1)
тогда эта производная называется ![]() -мерной плотностью распределения вероятностей случайного процесса. Основные свойства плотности (71.1) аналогичны свойствам плотности распределения вероятностей
-мерной плотностью распределения вероятностей случайного процесса. Основные свойства плотности (71.1) аналогичны свойствам плотности распределения вероятностей ![]() -мерного вектора. Рассмотрим основные из них.
-мерного вектора. Рассмотрим основные из них.
1) Функция распределения ![]() определяется через плотность:
определяется через плотность:
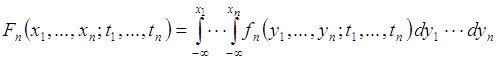 . (70.2)
. (70.2)
2) Плотность ![]() - неотрицательная функция:
- неотрицательная функция:
![]() . (70.3)
. (70.3)
3) Плотность удовлетворяет условию нормировки:
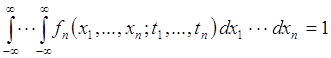 . (70.4)
. (70.4)
4) Выполняется равенство
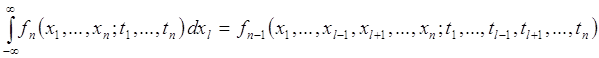 , (71.5)
, (71.5)
называемое свойством согласованности.
5) Плотность – симметричная функция относительно перестановок двух любых пар ![]() и
и ![]() :
:
![]() . (71.6)
. (71.6)
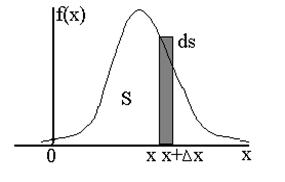
6) Плотность определяет вероятность попасть значениям случайного
процесса в заданные интервалы:
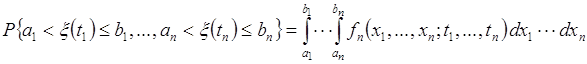 . (71.7)
. (71.7)
Моментные функции случайного процесса
72.1. Пусть ![]() - случайный процесс, имеющий плотность
- случайный процесс, имеющий плотность ![]() и
и ![]() функция
функция ![]() переменных. Вместо аргумента
переменных. Вместо аргумента ![]() ,
, ![]() , функции
, функции ![]() подставим
подставим ![]() . Тогда
. Тогда ![]() - случайная величина, математическое ожидание которой определяется соотношением:
- случайная величина, математическое ожидание которой определяется соотношением:
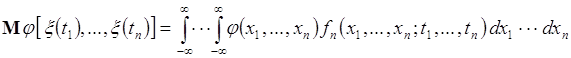 .
.
(72.1)
Рассмотрим простейшие примеры функции ![]() . 1) Пусть
. 1) Пусть ![]() - функция одной переменной, тогда
- функция одной переменной, тогда ![]() и (72.1) принимает вид:
и (72.1) принимает вид:
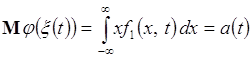 .
(72.2)
.
(72.2)
Функция ![]() называется математическим ожиданием (средним, статистическим средним) случайного процесса
называется математическим ожиданием (средним, статистическим средним) случайного процесса ![]() . 2) Аналогично выбор
. 2) Аналогично выбор ![]() приводит к равенству
приводит к равенству
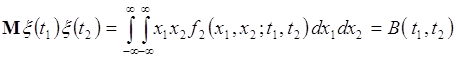 . (72.3)
. (72.3)
Функция ![]() называется корреляционной функцией случайного процесса
называется корреляционной функцией случайного процесса ![]() . 3) Аналогично вводятся дисперсия
. 3) Аналогично вводятся дисперсия
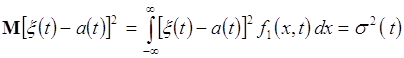 (72.4)
(72.4)
и ковариационная функцией случайного процесса
![]()
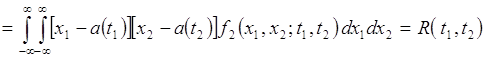 . (72.5)
. (72.5)
Получим соотношение, связывающее функции ![]() . Из (72.5) следует
. Из (72.5) следует
![]()
![]() . (72.6)
. (72.6)
Здесь использовалось равенство ![]() , поскольку
, поскольку ![]() - детерминированная функция и ее можно вынести за оператор математического ожидания. Таким образом, (72.6) принимает вид
- детерминированная функция и ее можно вынести за оператор математического ожидания. Таким образом, (72.6) принимает вид
![]() . (72.7)
. (72.7)
Похожие работы
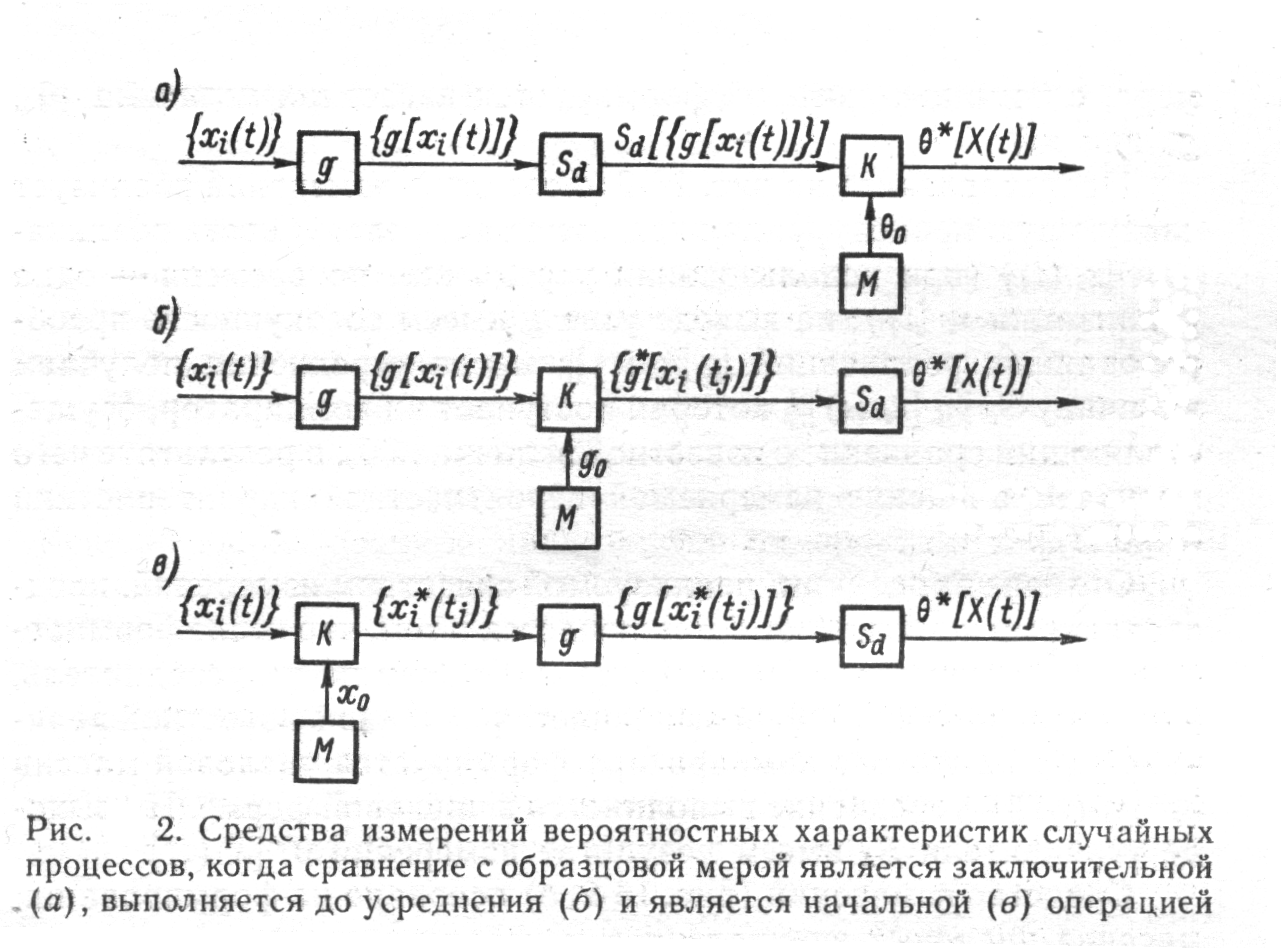
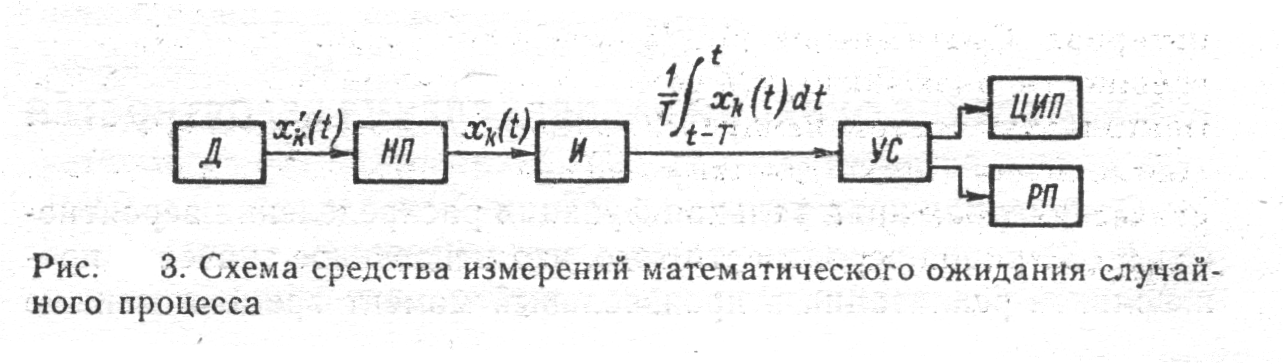
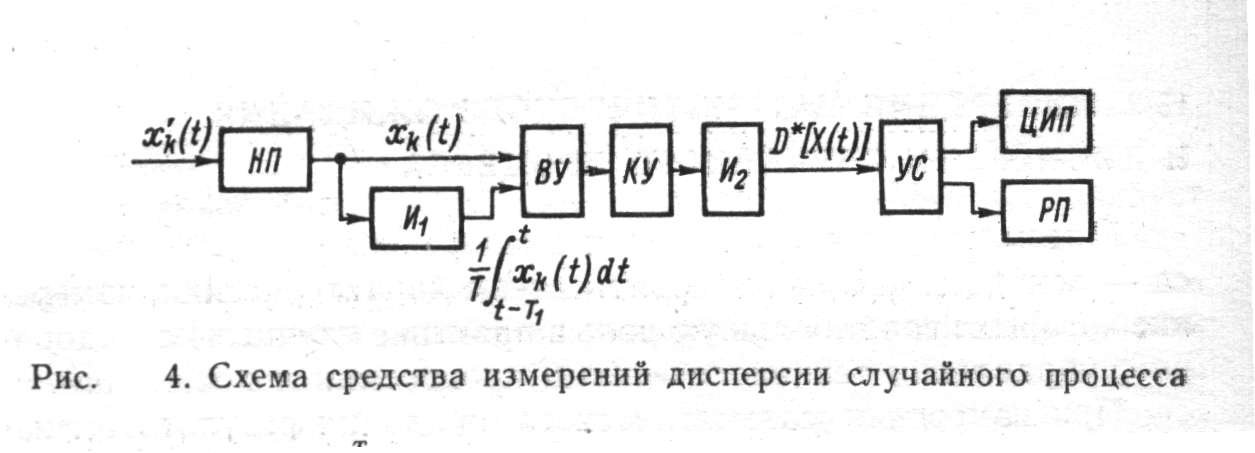
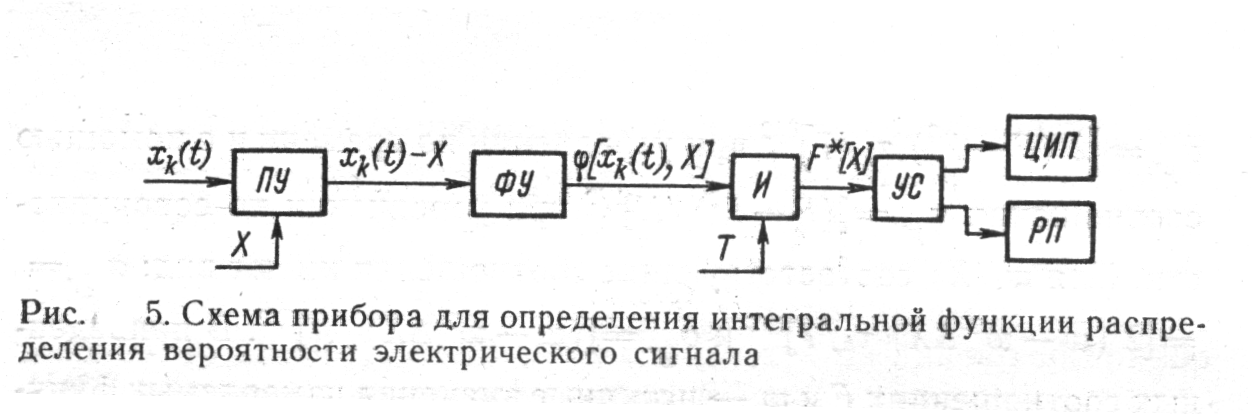
... описание производится с помощью систем вероятностных характеристик: многомерных функций распределения вероятности, моментных функций, характеристических функций и т. п. В теории статистических измерений исследуемый случайный процесс представляется своими реализациями, причем полное представление осуществляется с помощью так называемого ансамбля, т. е. бесконечной совокупностью реализаций. ...
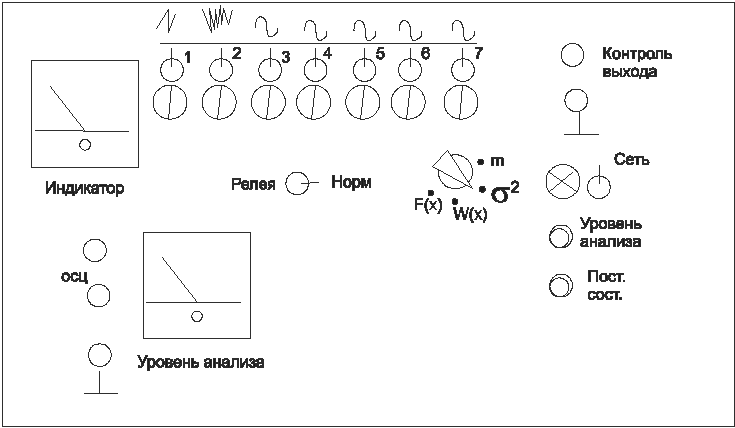
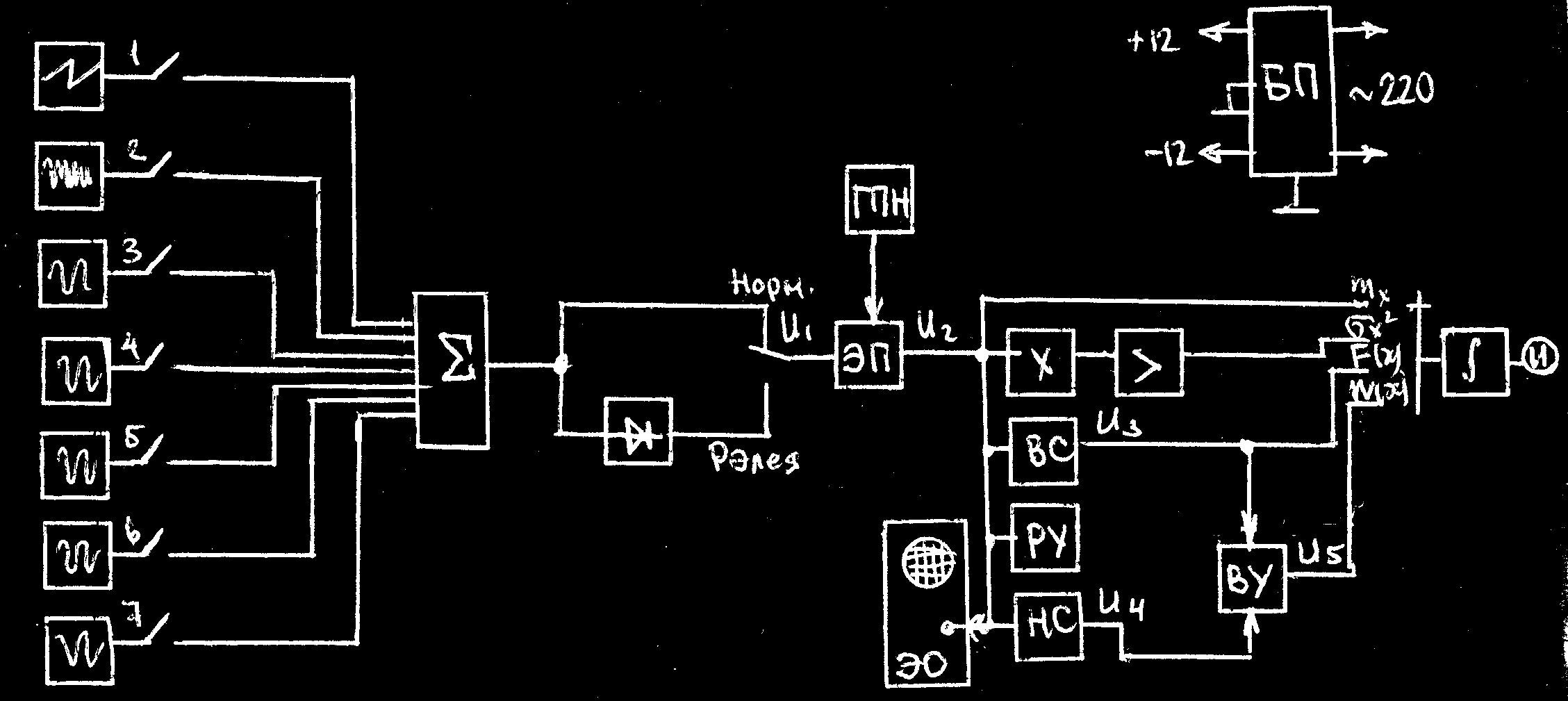
... функция и функция плотности и вероятности имеют следующий вид: Описание лабораторной установки Для выполнения работы необходимо использовать универсальный стенд для изучения законов распределения случайных процессов и электронный осциллограф. Передняя панель стенда Стенд включает в себя: - семь источников независимых случайных сигналов (одного шумового с нормальным распределением, ...
... ≠ j) X(t) = mx(t) + ∑ Viφi(t) (t ? T) Следует: K(t, t’) = ∑ Diφi(t)φi(t’) Эту формулу называют каноническим разложением корреляционной функции случайного процесса. В случае уравнения X(t) = mx(t) + ∑ Viφi(t) (t ? T) Имеют место формулы: X(t) = mx(t) + ∑ Viφ(t) ∫ x(τ)dt = ∫ mx(τ)dτ + ∑ Vi ...
... и реализация оптимальных в определенном смысле свойств системы по заданным статистическим свойствам входных сигналов. Статистическая динамика является разделом теории управления и базируется на теории вероятности и, в частности, на ее разделе теории случайных процессов. 1.1 Основные понятия теории вероятности Рассмотрим случайные величины и их характеристики. Случайное событие – это событие ...
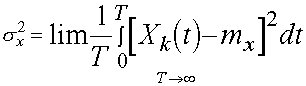
0 комментариев