Постановка задачи планирования производства в общем случае

3.1 Постановка задачи планирования производства в общем случае

Некоторое предприятие производит n типов продукции, затрачивая при этом m типов ресурсов. Известны следующие параметры: aij – количество i-го ресурса, необходимое для производства единичного количества j-й продукции; aij0 (i=1,…,m; j=1,…,n);

bi-запас i-го ресурса на предприятии, bi>0;

cj-цена единичного количества j-й продукции, cj>0.

Предполагается, что затраты ресурсов растут прямо пропорционально объему производства. Пусть xj – планируемый объем производства j-й продукции. Тогда допустимым является только такой набор производимой продукции x=(x1,x2,…,xn), при котором суммарные затраты каждого вида i-го ресурса не превосходят его запаса:

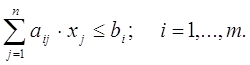 (1)

Кроме того, имеем следующее ограничение: xj0; j=1,…,n. (2)

Стоимость набора продукции x выражается величиной:  (3)

Задача планирования производства ставится следующим образом: среди всех векторов x, удовлетворяющим ограничениям (1), (2), найти такой, при котором величина (3) принимает наибольшее значение.

3.2 Математическое описание поставленной задачи планирования симплекс методом

Пусть некоторое предприятие производит 5 видов продукции A, B, C, D и E, затрачивая при этом 5 типов ресурсов. На производство продукции типа A требуется следующее количество имеющихся на предприятии ресурсов (дается количество каждого ресурса, необходимого для производства единицы продукции типа A): 1 – количество ресурса 1, 4 – количество ресурса 2, 2 – количество ресурса 3, 1 – количество ресурса 4, 3 – количество ресурса 5. На производство единицы продукции типа B требуется (в условных единицах): 2 – количество ресурса 1, 2 – количество ресурса 2, 1 – количество ресурса 3, 4 – количество ресурса 4, 2 – количество ресурса 5. На производство единицы продукции типа C требуется (в условных единицах): 4 – количество ресурса 1, 1 – количество ресурса 2, 3 – количество ресурса 3, 1 – количество ресурса 4, 2 – количество ресурса 5. На производство единицы продукции типа D требуется (в условных единицах): 3 – количество ресурса 1, 2 – количество ресурса 2, 4 – количество ресурса 3, 2 – количество ресурса 4, 1 – количество ресурса 5. На производство единицы продукции типа E требуется (в условных единицах): 1 – количество ресурса 1, 2 – количество ресурса 2, 1 – количество ресурса 3, 4 – количество ресурса 4, 4 – количество ресурса 5.

Допустим, что запас ресурса 1 на предприятии составляет 600 условных единиц, запас ресурса 2 – 590 условных единиц, запас ресурса 3 – 750 условных единиц, запас ресурса 4 – 670 условных единиц и запас ресурса 5 – 495 условных единиц.

Цена единицы продукции типа A равна 60 рублям, цена единицы продукции типа B равна 50 рублям, цена единицы продукции типа C равна 37 рублям, цена единицы продукции типа D равна 45 рублям, а единица продукции типа E – 56 рублям.

Нужно спланировать такой набор производимой продукции x=(x1, x2, x3, x4, x5), при котором суммарные затраты каждого вида ресурса не превосходят его запаса, т.е.

x1+4x2+2x3+1x4+3x5600;

2x1+2x2+x3+4x4+2x5590;

4x1+x2+3x3+x4+2x5750;

3x1+2x2+4x3+2x4+x5670;

x1+2x2+x3+4x4+4x5495;

и при этом должны выполняться следующие ограничения: x1, x2, x3, x4, x5  0. Спланированный набор производимой продукции x=(x1, x2, x3, x4, x5) должен обеспечить максимум стоимости данного набора

{60x1+50x2+37x3+45x4+56x5}max.

Таким образом, мы получим однокритериальную задачу, которая является задачей линейного программирования (ЗЛП). Она сводится к поиску экстремума линейной функции (данная функция называется либо критерием, либо целевой функцией)

f(x)=60x1+50x2+37x3+45x4+56x5

при наличии системы линейных неравенств, ограничивающих область изменения аргументов этой функции

x1+4x2+2x3+1x4+3x5600;

2x1+2x2+x3+4x4+2x5590;

4x1+x2+3x3+x4+2x5750;

3x1+2x2+4x3+2x4+x5670;

x1+2x2+x3+4x4+4x5495;

x1, x2, x3, x4, x5  0.

Похожие работы

Решение задач линейного программирования симплекс методом

Скачать

36149

6

0

... положит в такой симплекс-таблице текущие базисные переменные равными Ai,0, а свободные - нулю, то будет получено оптимальное решение. Практика применения симплекс метода показала, что число итераций, требуемых для решения задачи линейного программирования обычно колеблется от 2m до 3m, хотя для некоторых специально построенных задач вычисления по правилам симплекс метода превращаются в прямой ...

Построение экономической модели c использованием симплекс-метода

Скачать

81361

18

7

... определение базисных решений соответст- вует идентификации экстремальных точек , осуществляемой при геометрическом представлении пространства решений . Таким об- разом , максимальное число итераций при использовании симплекс- метода равно максимальному числу базисных решений задачи ЛП , представленной в стандартной форме . Это означает , что количество итерационных процедур симплекс-метода не ...

Симплекс метод в форме презентации

Скачать

25716

1

1

... - метод для решения задач линейного программирования. Задачи курсовой заботы: 1.         привести теоретический материал; 2.         на примерах рассмотреть симплекс метод; 3.         представить данную курсовую работу в виде презентации. Математическое программирование Математическое программирование занимается изучение экстремальных задач и поиском методов их решения. Задачи ...

Использование линейного программирования для решения задач оптимизации

Скачать

26852

2

4

... предложен в середине 1940-х годов Джорджем Данцигом, одним из основателей линейного программирования, еще до того, как компьютеры были использованы для решения линейных задач оптимизации. Формулировка задачи линейного программирования Нужно максимизировать при условиях при i = 1, 2, 3, . . ., m.. Иногда на xi также накладывается некоторый набор ограничений в виде равенств, но от ...