Навигация
Вычисление оптимальных стратегий на примере решения задач
2.1 Вычисление оптимальных стратегий на примере решения задач
Используя теорему о минимаксе, можно утверждать, что каждая антагонистическая игра имеет оптимальные стратегии.
Теорема: пусть А – матричная игра и строки ![]() данной матрицы являются доминирующими. Тогда игрок 1 имеет такую оптимальную стратегию х, что
данной матрицы являются доминирующими. Тогда игрок 1 имеет такую оптимальную стратегию х, что ![]() ; кроме того, любая оптимальная стратегия для игры, получающаяся в результате удаления доминирующих строк, будет также оптимальной для первоначальной игры.
; кроме того, любая оптимальная стратегия для игры, получающаяся в результате удаления доминирующих строк, будет также оптимальной для первоначальной игры.
Пример 1. Игра доминирования
Рассмотрим игру с матрицей 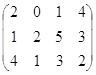 . Здесь второй столбец доминирует 4 и игрок 2 соответственно не будет использовать 4 стратегию. Поэтому можно рассмотреть матрицу следующего вида
. Здесь второй столбец доминирует 4 и игрок 2 соответственно не будет использовать 4 стратегию. Поэтому можно рассмотреть матрицу следующего вида 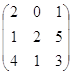 . В этой матрице третья строка доминирует первую. При удалении получается матрица
. В этой матрице третья строка доминирует первую. При удалении получается матрица ![]() . А в этой матрице третий столбец доминируется вторым. Следовательно, исходная матрица сводится к следующей матрице
. А в этой матрице третий столбец доминируется вторым. Следовательно, исходная матрица сводится к следующей матрице ![]() .
.
Пример 2. Игра на уклонение.
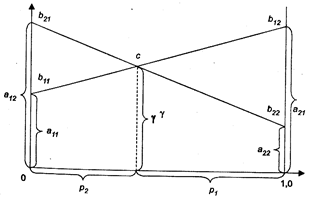
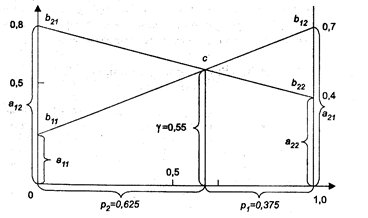
Предполагается, что игроки выбирают целые числа i и j между 1 и n, а игрок 1 выигрывает величину ![]() , т.е. расстояние между i и j. Пусть первый игрок придерживается стратегии
, т.е. расстояние между i и j. Пусть первый игрок придерживается стратегии ![]() , тогда
, тогда ![]() для всех
для всех ![]() ((
((![]() - значение игры).
- значение игры).
· Пусть ![]() нечётно, тогда игрок 2 имеет чистую стратегию
нечётно, тогда игрок 2 имеет чистую стратегию ![]() для всех
для всех ![]()
· Предположим, что ![]() чётно, тогда игрок 2 имеет такую стратегию
чётно, тогда игрок 2 имеет такую стратегию ![]() где
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() для всех
для всех ![]() . Теперь используя теорему можно убедиться, что значение игры
. Теперь используя теорему можно убедиться, что значение игры ![]() . Игрок 1 имеет оптимальную стратегию
. Игрок 1 имеет оптимальную стратегию ![]() , а оптимальная стратегия игрока 2 равна
, а оптимальная стратегия игрока 2 равна ![]() , если
, если ![]() и
и ![]() если
если ![]()
Приведём теорему, по которой решалась эта игра. Теорема: для того, чтобы ситуация ![]() была равновесной в игре
была равновесной в игре ![]() , а число
, а число ![]() - значение игры
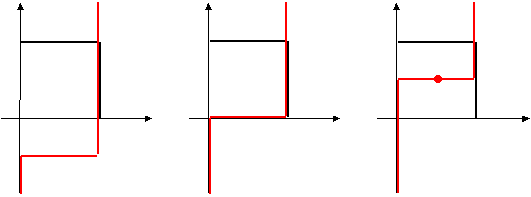
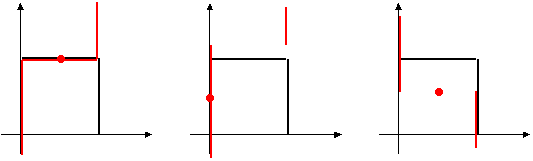
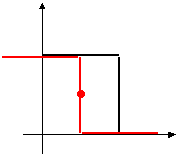
- значение игры ![]() , необходимо и достаточно выполнение следующего неравенства. Для всех
, необходимо и достаточно выполнение следующего неравенства. Для всех ![]() и
и ![]() :
: ![]() ).
).
Ситуация ![]() называется ситуацией равновесия в чистых стратегиях, если для любых
называется ситуацией равновесия в чистых стратегиях, если для любых ![]() выполнено двойное неравенство
выполнено двойное неравенство ![]() (*). Если каждый из игроков стремится достичь ситуации равновесия, то принцип, которому они следуют, называют принципом равновесия. Для игры, заданной матрицей
(*). Если каждый из игроков стремится достичь ситуации равновесия, то принцип, которому они следуют, называют принципом равновесия. Для игры, заданной матрицей ![]() равенство
равенство ![]() (т.е. верхнее значение игры равно нижнему значению) записывается в виде
(т.е. верхнее значение игры равно нижнему значению) записывается в виде ![]() , а неравенство (*) – в виде
, а неравенство (*) – в виде ![]() , где
, где ![]() чистые максиминная и минимаксная стратегии соответственно игроков I и I I.
чистые максиминная и минимаксная стратегии соответственно игроков I и I I.
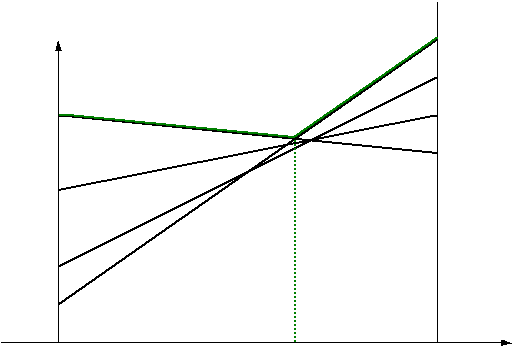
Пример 3. Игра «Дуэль».
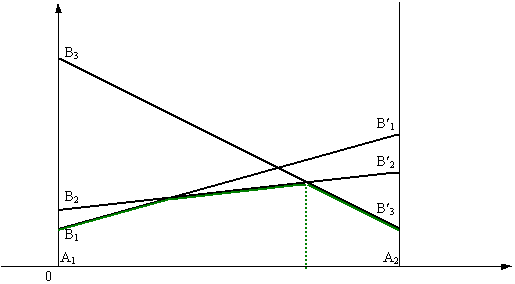
Два дуэлянта (игроки А и В) начинают сходиться в момент времени t=0. Встреча произойдёт в момент времени t=1. У каждого есть возможность выстрелить в любой момент времени. Если одному из них удастся выстрелить раньше соперника, то он становится победителем. Если же оба выстрелят одновременно, то дуэль закончится вничью. Если игрок А произведёт выстрел в момент времени x (![]() ) то его выстрел будет успешным с вероятностью р(x). Подобным образом будет вероятным выстрел игрока В в момент времени y (
) то его выстрел будет успешным с вероятностью р(x). Подобным образом будет вероятным выстрел игрока В в момент времени y (![]() ) c вероятностью q(y). При условии
) c вероятностью q(y). При условии ![]() игрок А выиграет с вероятностью р(x), а проиграет с вероятностью (1- р(x)) q(y). Тем самым его средний выигрыш при
игрок А выиграет с вероятностью р(x), а проиграет с вероятностью (1- р(x)) q(y). Тем самым его средний выигрыш при ![]() будет равен
будет равен ![]() . С другой стороны, если x> y, то его средний выигрыш будет равен
. С другой стороны, если x> y, то его средний выигрыш будет равен ![]() . При x= y средний выигрыш
. При x= y средний выигрыш ![]() . Таким образом, функция H(x,y) игрока А имеет вид
. Таким образом, функция H(x,y) игрока А имеет вид
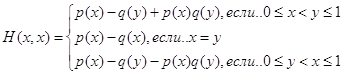
и антагонистическая игра задана. В частности, если игроки стреляют без промаха,
![]() ,
, 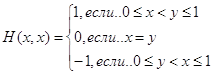
Похожие работы
... смешанными стратегиями игроков 1 и 2 называются такие наборы хо, уо соответственно, которые удовлетворяют равенству Е (А, х, y) = Е (А, х, y) = Е (А, хо, уо). Величина Е (А, хо ,уо) называется при этом ценой игры и обозначается через u. Имеется и другое определение оптимальных смешанных стратегий: хо, уо называются оптимальными смешанными стратегиями соответственно игроков 1 и 2, если они ...
... входить в его оптимальную стратегию с положительной вероятностью, если для них выполняется равенство М(х, yo) = V. Такие чистые стратегии х называются существенными. Теорема 5. Пусть дана бесконечная антагонистическая игра с непрерывной и дифференцируемой по y на единичном квадрате при любом х функцией выигрышей М(х, y), с оптимальной чистой стратегией yo игрока 2 и ценой игры V, тогда : 1) ...
... игроков не только на максимизацию своего выигрыша, сколько на минимизацию выигрыша противника. С другой стороны, естественно также рассматривать подходящим поведение игроков в конечных бескоалиционных играх, направленное на максимизацию своего выигрыша с учётом максимального противодействия игрока, т.е. подходящей стратегией игрока 1 считать оптимальную смешанную стратегию игрока 1 в матричной ...
... общую цель. Однако разные члены коллектива могут быть по-разному информированы об обстановке проведения игры. Выигрыш или проигрыш сторон оценивается численно, другие случаи в теории игр не рассматриваются, хотя не всякий выигрыш в действительности можно оценить количественно. Игрок - одна из сторон в игровой ситуации. Стратегия игрока - его правила действия в каждой из возможных ситуаций игры. ...
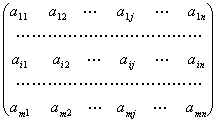
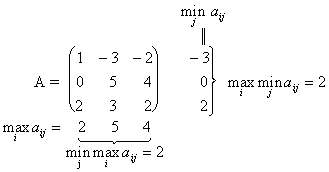
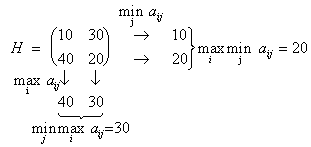
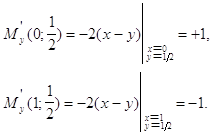
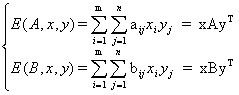
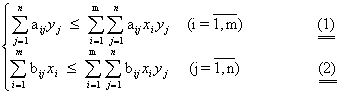
0 комментариев