Навигация
Классификация игр
1.3 Классификация игр
Различные виды игр можно классифицировать, основываясь на том или ином принципе: по числу игроков, по числу стратегий, по свойствам функций выигрыша, по возможности предварительных переговоров и взаимодействия между игроками в ходе игры. В зависимости от числа игроков различают игры с двумя, тремя и более участниками. Согласно другому принципу классификации (по количеству стратегий) различают конечные и бесконечные игры. В конечных играх игроки располагают конечным числом возможных стратегий (например, в игре в орлянку игроки имеют по два возможных хода - они могут выбрать "орел" или "решку"). Сами стратегии в конечных играх нередко называются чистыми стратегиями (смысл этого названия будет ясен далее).
Соответственно, в бесконечных играх игроки имеют бесконечное число возможных стратегий. Так в ситуации «Продавец-Покупатель» каждый из игроков может назвать любую устраивающую его цену и количество продаваемого (покупаемого) товара. Третий способ классификации игр-по свойствам функции выигрыша (платежных функций). Важным случаем в теории игр является ситуация, когда выигрыш одного из игроков равен проигрышу другого, т.е. налицо прямой конфликт между игроками. Подобные игры называются играми с нулевой суммой, или антагонистическими играми. Игры в орлянку или в шахматы - типичные примеры антагонистических игр. Прямой противоположностью играм такого типа являются игры с постоянной разностью, в которых игроки и выигрывают, и проигрывают одновременно, так что им выгодно действовать сообща. Между этими крайними случаями имеется множество игр с ненулевой суммой, где имеются и конфликты, и согласованные действия игроков. Можно также выделить 2 способа задания игры.
1 так называемая позиционная форма. При этом определяются:
· порядок ходов
· альтернативы (возможные ходы), доступные каждому из игроков на момент наступления его хода
· информация, которой владеет каждый из игроков на момент очередного хода
· выигрыши (для каждого игрока) как функции от выбранных ходов
· вероятностные распределения на множестве возможных состояний внешней среды
2. нормальная или стратегическая форма. Каждый участник (игрок) k, где![]() , характеризуется наличием индивидуальной системы целевых установок и множеством стратегий
, характеризуется наличием индивидуальной системы целевых установок и множеством стратегий ![]() , т.е. возможных вариантов действий в игре.
, т.е. возможных вариантов действий в игре.
Ранее упоминалось о таком понятии, как «антагонистическая игра». Примером такой игры может служить игра «Орлянка». Дадим определение антагонистической игре.
Антагонистическая игра - игра, в которой участвуют два игрока (обычно обозначаемые I и II) с противоположными интересами. Для антагонистической игры характерно, что выигрыш одного игрока равен проигрышу другого и наоборот, поэтому совместные действия игроков, их переговоры и соглашения лишены смысла.. Определяются антагонистические игры заданием множеств стратегий игроков и выигрышей игрока I в каждой ситуации, состоящей в выборе игроками своих стратегий. Таким образом, формально антагонистическая игра есть тройка ‹А, В, Н›, в которой А и В - множества стратегий игроков, а Н (а, b) - вещественная функция (функция выигрыша) от пар (а, b), где а A, b В. Игрок I, выбирая а, стремится максимизировать Н(а, b), а игрок II, выбирая b, - минимизировать Н (а, b).
Пример 2:
Рассмотрим игру G (4х5) в матричной форме.
|
|
|
|
|
| |
|
| 3 | 4 | 5 | 2 | 3 |
|
| 1 | 8 | 4 | 3 | 4 |
|
| 10 | 3 | 1 | 7 | 6 |
|
| 4 | 5 | 3 | 4 | 8 |
Очевидно надо выбирать ту стратегию, при которой выигрыш максимален. (Это так называемый принцип минимакса. О нём чуть позже). В правом добавочном столбце запишем минимальное значение выигрыша в каждой строке; обозначим его для i-ой строки ![]() .
.
|
|
|
|
|
|
| |
|
| 3 | 4 | 5 | 2 | 3 | 2 |
|
| 1 | 8 | 4 | 3 | 4 | 1 |
|
| 10 | 3 | 1 | 7 | 6 | 1 |
|
| 4 | 5 | 3 | 4 | 8 | 3 |
|
| 10 | 8 | 5 | 7 | 8 |
Из всех значений ![]() выделено наибольшее (3). Ему соответствует величина
выделено наибольшее (3). Ему соответствует величина ![]() - гарантированный выигрыш, который называется нижней ценой игры. Исходя из принципа осторожности, надо выбрать стратегию
- гарантированный выигрыш, который называется нижней ценой игры. Исходя из принципа осторожности, надо выбрать стратегию ![]() , а противник должен выбрать стратегию
, а противник должен выбрать стратегию ![]() . Такая стратегия называется «минимаксной». Выше было упомянуто о принципе минимакса. Рассмотрим далее соответствующую терему.
. Такая стратегия называется «минимаксной». Выше было упомянуто о принципе минимакса. Рассмотрим далее соответствующую терему.
Теорема о минимаксе.
Можно доказать, что для любой функции F(x,y) определённой на произвольном декартовом произведении X × Y имеет место неравенство ![]() . Отсюда следует, что
. Отсюда следует, что ![]()
Запишем 2 утверждения:
Утверждение 1. Точка 0 (в m-мерном пространстве) содержится в выпуклой оболочке m+n точек
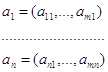 и
и 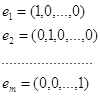
Утверждение 2. Существуют числа ![]() удовлетворяющие условиям
удовлетворяющие условиям ![]()
Доказательство: Пусть А – матричная игра. Имеет место либо утверждение 1, либо утверждение 2. Если верно утверждение 1 то 0 является выпуклой линейной комбинацией m+n векторов. Поэтому существуют такие
![]() что
что 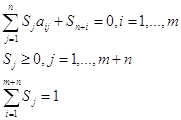
Если бы все числа ![]() были бы равны нулю, то 0 оказывался бы выпуклой линейной комбинацией m единичных векторов
были бы равны нулю, то 0 оказывался бы выпуклой линейной комбинацией m единичных векторов ![]() , что невозможно, т.к. они линейно независимы. Следовательно, по крайней мере одно из чисел
, что невозможно, т.к. они линейно независимы. Следовательно, по крайней мере одно из чисел ![]() положительно и
положительно и
![]()
тогда можно положить
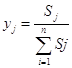 и получится
и получится 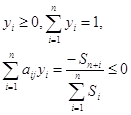 для всех i
для всех i
Значит ![]() и
и ![]()
Предположим, что верно утверждение 2. Тогда ![]() , так что
, так что ![]() . Следовательно, неравенство
. Следовательно, неравенство ![]() не имеет смысла. Предположим, что игра А изменена на игру
не имеет смысла. Предположим, что игра А изменена на игру ![]() , где
, где ![]() . Для любых х и y
. Для любых х и y ![]() , поэтому
, поэтому ![]() . Так как неравенство
. Так как неравенство ![]() не имеет смысла, то неравенство
не имеет смысла, то неравенство ![]() также не выполняется. Но k произвольно. Значит неравенство
также не выполняется. Но k произвольно. Значит неравенство ![]() невозможно. Т.к.
невозможно. Т.к. ![]() то
то ![]() . Что и требовалось доказать.
. Что и требовалось доказать.
Принцип минимакса.
Рассмотрим игру ![]() с платежной матрицей
с платежной матрицей ![]() Следует определить наилучшую стратегию игрока I среди стратегий
Следует определить наилучшую стратегию игрока I среди стратегий ![]() ,
, ![]() и игрока II среди стратегий
и игрока II среди стратегий ![]() ,
, ![]() . Определение наилучших стратегий игроков основано на принципе, который предполагает, что противники, участвующие в игре, одинаково разумны и каждый из них делает все для того, чтобы добиться своей цели. Найдем наилучшую стратегию игрока I. Допустим, что он выбрал i-ю стратегию (i –ю строку матрицы (1)). Тогда он получит меньше, чем
. Определение наилучших стратегий игроков основано на принципе, который предполагает, что противники, участвующие в игре, одинаково разумны и каждый из них делает все для того, чтобы добиться своей цели. Найдем наилучшую стратегию игрока I. Допустим, что он выбрал i-ю стратегию (i –ю строку матрицы (1)). Тогда он получит меньше, чем ![]() – наименьшее число в этой строке. Причем это будет в том случае, если игрок II каким-то образом раскроет стратегию игрока I. Из сказанного следует, что I игрок, если он не желает рисковать, т.е. играть не оптимально, должен действовать следующим образом – определить наименьшие элементы всех строк и выбрать ту из них, в которой это число наибольшее. В этом случае он гарантирует себе выигрыш равный наибольшему из меньших чисел всех строк. Этот выигрыш равен
– наименьшее число в этой строке. Причем это будет в том случае, если игрок II каким-то образом раскроет стратегию игрока I. Из сказанного следует, что I игрок, если он не желает рисковать, т.е. играть не оптимально, должен действовать следующим образом – определить наименьшие элементы всех строк и выбрать ту из них, в которой это число наибольшее. В этом случае он гарантирует себе выигрыш равный наибольшему из меньших чисел всех строк. Этот выигрыш равен ![]() Число
Число ![]() это “низкий выигрыш” игрока I и его называют нижним значением или нижней ценой игры. Как же рассуждает второй игрок? “Если я выберу j-ую стратегию (j-ый столбец), то самый лучший выигрыш у игрока I будет
это “низкий выигрыш” игрока I и его называют нижним значением или нижней ценой игры. Как же рассуждает второй игрок? “Если я выберу j-ую стратегию (j-ый столбец), то самый лучший выигрыш у игрока I будет ![]() наибольшее число этого столбца. Чтобы рисковать, я должен выбрать столбец, в котором это число наименьшее. В результате I игрок не сможет получить больше, чем
наибольшее число этого столбца. Чтобы рисковать, я должен выбрать столбец, в котором это число наименьшее. В результате I игрок не сможет получить больше, чем ![]() Число
Число ![]() представляет собой ”верхний выигрыш” игрока I и называется верхним значение или верхней ценой игры. Можно показать, что для всякой матричной игры выполняется условие
представляет собой ”верхний выигрыш” игрока I и называется верхним значение или верхней ценой игры. Можно показать, что для всякой матричной игры выполняется условие ![]() . Если
. Если ![]() , то такие игры называются играми с седловой точкой. Из неравенства
, то такие игры называются играми с седловой точкой. Из неравенства ![]() следует, что
следует, что ![]() . Это фактически означает, игрок I мог бы рассчитывать на выигрыш
. Это фактически означает, игрок I мог бы рассчитывать на выигрыш ![]() .
.
Похожие работы
... смешанными стратегиями игроков 1 и 2 называются такие наборы хо, уо соответственно, которые удовлетворяют равенству Е (А, х, y) = Е (А, х, y) = Е (А, хо, уо). Величина Е (А, хо ,уо) называется при этом ценой игры и обозначается через u. Имеется и другое определение оптимальных смешанных стратегий: хо, уо называются оптимальными смешанными стратегиями соответственно игроков 1 и 2, если они ...
... входить в его оптимальную стратегию с положительной вероятностью, если для них выполняется равенство М(х, yo) = V. Такие чистые стратегии х называются существенными. Теорема 5. Пусть дана бесконечная антагонистическая игра с непрерывной и дифференцируемой по y на единичном квадрате при любом х функцией выигрышей М(х, y), с оптимальной чистой стратегией yo игрока 2 и ценой игры V, тогда : 1) ...
... игроков не только на максимизацию своего выигрыша, сколько на минимизацию выигрыша противника. С другой стороны, естественно также рассматривать подходящим поведение игроков в конечных бескоалиционных играх, направленное на максимизацию своего выигрыша с учётом максимального противодействия игрока, т.е. подходящей стратегией игрока 1 считать оптимальную смешанную стратегию игрока 1 в матричной ...
... общую цель. Однако разные члены коллектива могут быть по-разному информированы об обстановке проведения игры. Выигрыш или проигрыш сторон оценивается численно, другие случаи в теории игр не рассматриваются, хотя не всякий выигрыш в действительности можно оценить количественно. Игрок - одна из сторон в игровой ситуации. Стратегия игрока - его правила действия в каждой из возможных ситуаций игры. ...
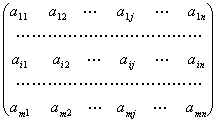
0 комментариев