Навигация
Статистичні оцінки параметрів розподілу
5. Статистичні оцінки параметрів розподілу
Нехай необхідно вивчити кількісну ознаку X генеральної сукупності. І нехай відомий вигляд розподілу цієї кількісної ознаки. Необхідно знайти параметри цього розподілу за статистичними даними вимірювань або спостережень. Приклад 3.1.Якщо відомо наперед, що ознака генеральної сукупності розподілена нормально, то необхідно оцінити параметриНехай ![]() значення кількісної ознаки X , які одержані в результаті n спостережень. Від серії до серії спостережень, взагалі кажучи, одержуються різні значення
значення кількісної ознаки X , які одержані в результаті n спостережень. Від серії до серії спостережень, взагалі кажучи, одержуються різні значення ![]() . Тому останні мають розглядатися як значення випадкових величин
. Тому останні мають розглядатися як значення випадкових величин ![]() . Щоб знайти точкову оцінку (точкова оцінка виражається одним числом) невідомого параметра (знайти наближенне значення) необхідно знайти функцію цих випадкових величин, значення якої при їх конкретних значеннях
. Щоб знайти точкову оцінку (точкова оцінка виражається одним числом) невідомого параметра (знайти наближенне значення) необхідно знайти функцію цих випадкових величин, значення якої при їх конкретних значеннях ![]() було б значенням точкової оцінки невідомого параметра розподілу.
було б значенням точкової оцінки невідомого параметра розподілу.
Отже, статистичною точковою оцінкою невідомого параметра теоретичного розподілу називають функцію випадкових величин![]() . В подальшому точкова статистична оцінка буде називатися просто статистичною оцінкою.
. В подальшому точкова статистична оцінка буде називатися просто статистичною оцінкою.
Нехай q - параметр теоретичного розподілу і ![]() його статистична оцінка. Статистична оцінка називається незміщеною, якщо її математичне сподівання дорівнює значенню параметра при будь-якому об’ємі вибірки, тобто якщо
його статистична оцінка. Статистична оцінка називається незміщеною, якщо її математичне сподівання дорівнює значенню параметра при будь-якому об’ємі вибірки, тобто якщо
![]() ,
,
і зміщеною якщо
![]() .
.
Використання зміщеної оцінки приводить до систематичних похибок одного знаку. Цього немає при використанні незміщеної оцінки.
Але незміщена оцінка не завжди дає необхідну точність визначення значення параметра теоретичного розподілу. Для цього необхідно, щоб вона була ефективною, а при великих об’ємах вибірок і умотивованою. Статистична оцінка називається ефективною, якщо при заданному об’ємі вибірки має найменшу можливу дисперсію. Статистична оцінка є умотивованою, якщо при ![]() по ймовірності прямує до параметра теоретичного розподілу. Якщо дисперсія незміщенної оцінки при
по ймовірності прямує до параметра теоретичного розподілу. Якщо дисперсія незміщенної оцінки при ![]() прямує до нуля, то така оцінка є умотивованою.
прямує до нуля, то така оцінка є умотивованою.
При малих об’ємах вибірки точкова оцінка може значно відрізнятися від значення параметра теоретичного розподілу. З цієї причини при малих об’ємах вибірок користуються інтервальними оцінками.
Інтервальною називають оцінку, яка визначається двома числами – кінцями інтервала. Інтервальна оцінка дозволяє встановити точність та надійність оцінок.
Нехай ![]() значення оцінки
значення оцінки ![]() для конкретної вибірки.
для конкретної вибірки. ![]() тим точніше визначає значення параметра q, чим менша абсолютна різниця
тим точніше визначає значення параметра q, чим менша абсолютна різниця ![]() . Нехай d>0 - деяке число. Ймовірність
. Нехай d>0 - деяке число. Ймовірність
![]() (1)
(1)
називається надійністю оцінки ![]() . Рівність (1) можна переписати у вигляді
. Рівність (1) можна переписати у вигляді
![]() ,
,
![]() .
.
Виходить, що ймовірність того, що випадковий інтервал ![]() покриває невідоме значення параметра q дорівнює g. Такий інтервал називається довірчим. Отже, інтервальна оцінка визначається довірчим інтервалом та надійністю. Чим менша надійність, тим вужчий довірчий інтервал, і навпаки. На практиці надійність задається близькою да 1. Найбільш часто задають надійності 0.95,0.99 і 0.999.
покриває невідоме значення параметра q дорівнює g. Такий інтервал називається довірчим. Отже, інтервальна оцінка визначається довірчим інтервалом та надійністю. Чим менша надійність, тим вужчий довірчий інтервал, і навпаки. На практиці надійність задається близькою да 1. Найбільш часто задають надійності 0.95,0.99 і 0.999.
6.Статистичні оцінки чисельних характеристик дискретних розподілів
Нехай X дискретна випадкова величина із розподілом
![]() .(1.2)
.(1.2)
Множина значень випадкової величини X є генеральною сукупністю і вважається відомою.
Приклад 4.1.1. Кількість очок, яка випадає при киданні несиметричного кубика є дискретною випадковою величиною з розподілом
![]()
з відомими значеннями та невідомими ймовірностями.
Нехай потрібно знайти математичне сподівання ![]() випадкової величини X (яке в математичній статистиці називається генеральним середнім і позначається
випадкової величини X (яке в математичній статистиці називається генеральним середнім і позначається ![]() ) та дисперсію
) та дисперсію ![]() (генеральну дисперсією
(генеральну дисперсією ![]() ). Для цього здійснюють вибірку об’єму n.
). Для цього здійснюють вибірку об’єму n.
Статистичною оцінкою генерального середнього є випадкова величина
![]() ,(1.3)
,(1.3)
де ![]() – дискретна випадкова величина – кількість значень
– дискретна випадкова величина – кількість значень ![]() у вибірці. Вона може набувати значень від 0 до n. Статистична оцінка
у вибірці. Вона може набувати значень від 0 до n. Статистична оцінка![]() є незміщенною (
є незміщенною (![]() ), ефективною та умотивованною.
), ефективною та умотивованною.
Доведення. Якщо вважати, що вибірка здійснюється по одному, то випадкову величину ![]() можна також представити як суму випадкових величин
можна також представити як суму випадкових величин ![]() - варіанта при
- варіанта при ![]() -вийманні, кожна з яких має розподіл, який співпадає з розподілом випадкової величини
-вийманні, кожна з яких має розподіл, який співпадає з розподілом випадкової величини ![]() :
:
![]()
Тому для математичного сподівання випадкової величини ![]() можна записати
можна записати
![]()
З врахуванням того, що випадкові величини ![]() мають однаковий розподіл з випадковою величиною
мають однаковий розподіл з випадковою величиною ![]() можна записати, що
можна записати, що
![]() ,
,
і, як наслідок,
![]() .
.
Отже, статистична оцінка ![]() є незміщенною.
є незміщенною.
Дисперсії випадкових величин ![]() однакові. Якщо вони обмежені, то згідно теореми Чебишева (3.9.2.1
однакові. Якщо вони обмежені, то згідно теореми Чебишева (3.9.2.1
 ,
,
а це означає, що ![]() по ймовірності збігається до генерального середнього, що, у свою чергу, означає, що
по ймовірності збігається до генерального середнього, що, у свою чергу, означає, що ![]() є ефективною статистичною оцінкою генерального середнього.
є ефективною статистичною оцінкою генерального середнього.
Випадкова величина (вибіркова дисперсія)
![]() (1.4)
(1.4)
є зміщенною (![]() ) статистичною оцінкою дисперсії дискретної випадкової величини X – генеральної дисперсії. Тому для генеральної дисперсії використовується “виправлена” вибіркова дисперсія
) статистичною оцінкою дисперсії дискретної випадкової величини X – генеральної дисперсії. Тому для генеральної дисперсії використовується “виправлена” вибіркова дисперсія
![]() ,(1.5)
,(1.5)
яка є незміщенною (![]() ), ефективною та умотиванною.
), ефективною та умотиванною.
Різниця між вибірковою та “виправленною” вибірковою дисперсіями при достатньо великому об’ємі вибірки мала. На практиці користуються “виправленною” дисперсією , якщо приблизно ![]() .
.
Для оцінки середньоквадратичного відхилення генеральної сукупності (в цьому випадку - дискретної випадкової величини X) використовують “виправлене” середньоквадратичне відхилення вибірки
![]() ,(1.6)
,(1.6)
яка є незміщенною (![]() , sz – середньоквадратичне відхилення генеральної сукупності), ефективною та умотивованною.
, sz – середньоквадратичне відхилення генеральної сукупності), ефективною та умотивованною.
Статистичними оцінками ймовірностей ![]() є відносні частоти
є відносні частоти
![]() ,
,
які є незміщенними (![]() ), ефективними та умотивованими.
), ефективними та умотивованими.
Довірчі інтервали ймовірностей ![]() обчислюються за формулами
обчислюються за формулами
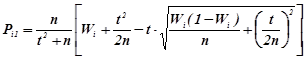 ,(1.7а)
,(1.7а)
 .(1.7b)
.(1.7b)
Значення змінної t (різне для кожного i) знаходиться з умови ![]() , де
, де ![]() - інтеграл Лапласа,
- інтеграл Лапласа, ![]() - надійність відносної частоти
- надійність відносної частоти ![]() як статистичної оцінки ймовірності pi.
як статистичної оцінки ймовірності pi.
Приклад 1.2. Несиметричний кубик кинули 80 разів і при цьому шість очок випало 16 разів. Знайти довірчий інтервал для невідомої ймовірності ![]() з надійністю 0.9
з надійністю 0.9
Розв’язування. За умовою задачі ![]() . Відносна частота
. Відносна частота ![]() .Значення змінної t знаходиться рівняння
.Значення змінної t знаходиться рівняння
![]() . Розв’язок рівняння
. Розв’язок рівняння ![]() . За формулами (4.1.6а) та (4.1.6b)
. За формулами (4.1.6а) та (4.1.6b)
 ,
,
 .
.
Отже, довірчий інтеграл для оцінки невідомої ймовірності ![]()
![]() з надійністю 0.9
з надійністю 0.9
Похожие работы
... ія розподілення експоненціального закону: , а імовірність попадання у інтервал (a,b) безперервної випадкової величини Х, розподіленою за експоненціальним законом дорівнює: . 2. Види типових задач з математичної статистики Тип 1 Ланка дослідів дала певну послідовність результатів. Вирахувати середнє значення виміряння, дисперсію, похибки, а також встановити закони розподілення ...
... необхідності допускається застосування байєсівських процедур. Байєсівський підхід стає все більш популярним в області фармакокінетики. Можна сказати, що клінічні дослідження мають ще тривалішу історію, ніж математична статистика. Клінічні дослідження в тому розумінні, що ми звикли вкладати в це поняття, в основному одержали розвиток після другої світової війни, хоча відомі і більш ранні приклади. ...
... ідому р і. Знайти функцію розподілу випадкової величини F(Х) та побудувати її графік. Обчислити математичне сподівання М(Х), дисперсію D(Х) та середнє квадратичне відхилення випадкової величини Х. Х 11 13 15 19 Р 0,18 0,32 0,4 ? Розв’язання Згідно з умовою нормування розподілу ймовірностей випадкової величини Звідси знаходимо : Функцію розподілу знаходимо на основі ...
... яким чином досягти певного рівня обслуговування (максимального скорочення черги або втрат вимог) при мінімальних витратах, пов'язаних з простоєм обслуговуючих устроїв. математичне моделювання економічний аналіз 2. Прийоми економічного аналізу на базі математичної статистики Застосування методів моделювання в аналітичному дослідженні господарської діяльності підприємств та їхніх структурних ...
0 комментариев