Навигация
Власні значення та власні вектори матриці
37560
знаков
25
таблиц
38
изображений
1.2 Власні значення та власні вектори матриці
Якщо А — квадратна матриця п-го порядку і 
при 
, то число l називається власним значенням матриці, а ненульовий вектор х — відповідним йому власним вектором. Перепишемо задачу в такому вигляді
(1)
Для існування нетривіального розв’язку задачі (1) має виконуватися умова
(2)
Цей визначник являє собою многочлен п-ї степені від l; його називають характеристичним многочленом. Значить, існує п власних значень — коренів цього многочлена, серед яких можуть бути однакові (кратні).
Якщо знайдено деяке власне значення, то, при підстановці його в однорідну систему (1), можна визначити відповідний власний вектор. Будемо нормувати власні вектори[1]. Тоді кожному простому (не кратному) власному значенню відповідає один (з точністю до напрямку) власний вектор, а сукупність всіх власних векторів, що відповідають сукупності простих власних значень, лінійно-незалежна. Таким чином, якщо всі власні значення матриці прості, то вона має п лінійно-незалежних власних векторів, які утворюють базис простору.
Кратному власному значенню кратності р може відповідати від 1 до р лінійно-незалежних власних векторів. Наприклад, розглянемо такі матриці четвертого порядку:
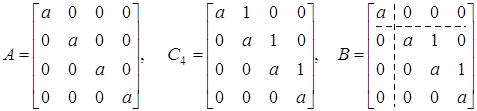(3)
В кожної з них характеристичне рівняння приймає вигляд 
, а отже, власне значення 
і має кратність р=4. Проте в першої матриці є чотири лінійно-незалежних власних вектора
(4)
У другої матриці є тільки один власний вектор е1. Другу матрицю називають простою жордановою (або класичною) підматрицею. Третя матриця має так звану канонічну жорданову форму (по діагоналі стоять або числа, або жорданові підматриці, а інші елементи дорівнюють нулеві).
Таким чином, якщо серед власних значень матриці є кратні, то її власні вектори не завжди утворюють базис. Однак і в цьому випадку власні вектори, що відповідають різним власним значенням, являються лінійно-незалежними.[3, стор 156]
При розв’язуванні теоретичних і практичних задач часто виникає потреба визначити власні значення даної матриці А, тобто обчислити корені її вікового (характеристичного) рівняння
det(A - lE) = 0 (2)
а також знайти відповідні власні векторі матриці А. Друга задача є простішою, оскільки якщо корені характеристичного рівняння відомі, то знаходження власних векторів зводиться до відшукання ненульових розв’язків деяких однорідних лінійних систем. Тому ми в першу чергу будемо займатися першою задачею — відшуканням коренів характеристичного рівняння (2).
Тут в основному застосовуються два прийоми: 1) розгортання вікового визначника в поліном n-го степеня
D(l) = det(A - lE)
з подальшим розв’язком рівняння D(l) = 0 одним з відомих наближених, взагалі кажучи, способів (наприклад, методом Лобачевського-Греффе) наближене визначення коренів характеристичного рівняння (найчастіше найбільших по модулю) методом ітерації, без попереднього розгортання вікового визначника.
Розгортання вікового визначника.
Як відомо, віковим визначником матриці А = [aij] називається визначник вигляду
D(l) = det(A - lE) = 
(1)
Прирівнюючи цей визначник до нуля, одержуємо характеристичне рівняння
D(l) = 0
Якщо потрібно знайти все коріння характеристичного рівняння, то доцільно заздалегідь обчислити визначник (1).
Розгортаючи визначник (1), одержуємо поліном n-го степеня
(2)
Де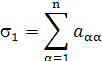 
є сума усіх діагональних мінорів першого порядку матриці А.
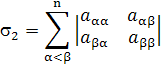
є сума всього діагонального мінору другого порядку матриці А;
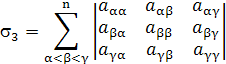
— сума всіх діагональних мінорів третього порядку матриці А і т.д. Нарешті
sn = det A.
Легко переконатися, що число діагональних мінорів k-го порядку матриці А дорівнює
(k = 1, 2, …, n ).
Звідси одержуємо, що безпосереднє обчислення коефіцієнтів характеристичного полінома (2) еквівалентно обчисленню
визначників різних порядків. Остання задача, взагалі кажучи, технічно важко здійснена для скільки-небудь великих значень n. Тому створені спеціальні методи розгортання вікових визначників (методи А. Н. Крилова, А. М. Данілевського, Леверье, метод невизначених коефіцієнтів, метод інтерполяції та ін.).
Розділ ІІ. Знаходження власних векторів і власних значень матриць
Похожие работы
... і простору матриця лінійного оператора має діагональний вид, то всі вектори базису є власними векторами оператора . Таким чином, доведено наступне твердження. Теорема 5.2. Для того, щоб матриця лінійного оператора у базисі простору була діагональною, необхідно і достатньо, щоб вектори були власними векторами оператора . Теорема 5.3. Якщо власні значення лінійного оператора , діючого в -мі ...
... йний оператор задається матрицею . Отже, при зафіксованому базисі кожному лінійному оператору простору відповідає певна квадратна матриця -го порядку – матриця цього оператора. 3. Власні вектори й власні значення лінійного оператора Означення 1. Підпростір лінійного простору називається інваріантним відносно оператора , якщо , тобто якщо образ будь-якого вектора із міститься в . ...
... і означення Означення: Дифуром називається рівняння, яку містить шукану похідну ф-ії. Найбільший порядок похідних називається порядком диф.рівняння. Означення матрець, типи матрець. Означення: Матрицею називається прямокутна таблиця чисел, яка має m рядків і n стовпчиків. Їх позначають великими літерами A,B,C і т.д. Типи матрець: Квадратна матриця, в якої елементи головної діагоналі дорівнюють ...
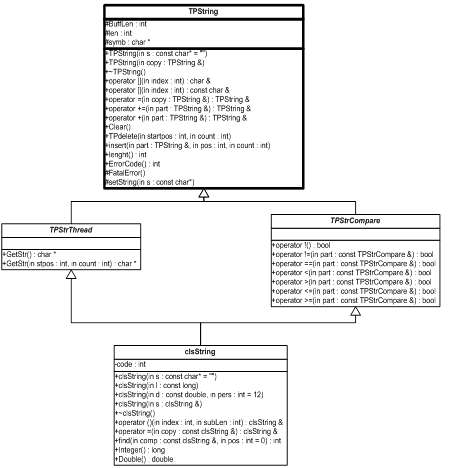
... ліворуч. Перевантажені операції помістити в потік і взяти з потоку повинні об’являтися як дружні, якщо вони повинні мати прямий доступ до закритих елементів класу з міркувань продуктивності. 2. Розробка власного класу clsString 2.1 Загальний алгоритм вирішення Створимо базовий клас TPString у якому розмістимо мінімальнонеобхідні компоненти, але при цьому цей клас вже буде функці ...
0 комментариев