Навигация
Примеры счетных множеств
3.5. Примеры счетных множеств
Множество целых чисел Z является счетным (Z ~ N).
Доказательство. Пронумеруем числа из Z:
| N | 1 | 2 | 3 | 4 | … |
| Z | 0 | -1 | 1 | 2 | … |
Рациональные числа R образуют счётное множество.
Доказательство.
Любое рациональное число можно представить в виде : ![]() , mZ, nN.
, mZ, nN.
Введем понятие высоты h рационального числа: h = |m| + n.
Каждой высоте соответствует конечное число рациональных чисел:
h = 1: ![]() .
.
h = 2: ![]() .
.
h = 3: ![]() .
.
h = 4 …
Приписывая последовательно этим рациональным числам номера 1, 2, 3… мы пронумеруем все рациональные числа. Следовательно, множество рациональных чисел счетно согласно определению.
3.6. Несчетные множества. Мощность континуума
Теорема. Мощность действительных чисел отрезка [0;1] больше чем счетное.
Доказательство (от противного).
Предположим, мощность отрезка [0;1] счетна. Т.е. можно установить взаимнооднозначное соответствие:
1 ~ 0.3751…
2 ~ 0.2151…
3 ~ 0.2216…
…
Построим число a из пронумерованных чисел согласно правилам:
Из первого числа возьмем первую цифру после запятой, из второго числа – вторую, из третьего – третью и так далее.
Если текущая цифра равна единице, то заменим ее на двойку. В противном случае цифру заменим на единицу.
В результате получим: a = 0.122…
a [0;1] и числу a соответствует nN.
Это противоречит тому, что, когда мы изменили a, мы изменили цифру, стоящую на n-ном десятичном месте. Следовательно, a не может стоять на n-ном месте. Следовательно, мы пришли к противоречию и, значит, мощность множества действительных чисел несчетна.
Мощность множества всех действительных чисел (или, что то же, множества всех точек числовой оси) обозначается символом c (“континуум”). Поскольку множество всех действительных чисел несчётно, то א0 < c.
Континуум – не самая большая из бесконечных мощностей. Так, мощность множества всех подмножеств точек числовой оси больше, чем мощность самого множества всех точек оси. Она обозначается 2c и называется гиперконтинуумом.
Глава 4. Аксиоматика теории множеств4.1. Аксиомы теории множеств
Современная теория множеств строится на системе аксиом — утверждений, принимаемых без доказательства, из которых выводятся все теоремы и утверждения теории множеств.
Система аксиом Цермело — Френкеля (ZF) является стандартной системой аксиом для теории множеств. Эта и подобные ей системы аксиом любопытны потому, что любая математическая теория может быть «переведена» на язык теории множеств таким образом, что теоремы этой теории станут теоремами о множествах, доказуемыми из аксиом ZF.
1. Аксиома объемности. Если два множества имеют одни и те же элементы, они тождественны.
"A, B: A=B Û "c, cÎAÛ cÎB.
2. Аксиома пустого множества. Существует пустое множество , которое не содержит элементов.
$: "a, aÏ.
3. Аксиома пары. Для любых множеств A и B существует множество C такое, что A и B являются его единственными элементами. Множество C обозначается {A, B} и называется неупорядоченной парой A и B. Если A = B, то C состоит из одного элемента.
"A, "B, $C: "D, DÍCÛ(D=A Ú D=B).
4. Аксиома объединения. Для любого множества A существует множество B=a1Èa2È…Èan – объединение всех элементов множества A, состоящее из тех и только тех элементов, которые содержатся в элементах множества А.
"A, $B: "C, CÍB Û $D, (CÍD Ù DÍA).
5. Аксиома бесконечности. Существует множество, которое содержит ∅ в качестве своего элемента, и такое, что если а есть элемент этого множества, тогда последовательность aÈ{a} есть также элемент этого множества.
$w: Îw Ù "x, xÎw Þ {x,{x}}Îw.
6. Аксиома регулярности. Если A – непустое множество, тогда имеется подмножество В множества A, такое, что не имеется множеств, которые принадлежат обоим множествам А и В.
7. Аксиома выделения. Любому множеству A и свойству j отвечает множество B, элементами которого являются те и только те элементы A, которые обладают свойством j.
"A $B: "c, cÎB Û (cÎA Ù j(c)).
8. Аксиома основания. Каждое непустое множество S содержит подмножество A такое, что SÇA=.
"S, S¹ Þ $A, AÍS Ù AÇS=.
9. Аксиома выбора. Для любого семейства попарно непересекающихся непустых множеств существует множество C такое, что, каково бы ни было множество X данного семейства, множество состоит из одного элемента.
Приведенный список аксиом не является каким-то каноническим. Возможны другие перечни и другие аксиомы.
Математики и философы, как уже было отмечено, расходятся в понимании основной цели аксиоматизации теории множеств. Многие полагают (это стало “учебной” точкой зрения), что суть аксиоматизации состоит в ограничении области множеств, с которыми математики уже имели и имеют дело, с целью недопущения парадоксов.
Аксиоматика теории множеств позволяет разрешить фундаментальную философскую проблему относительно природы математики. В аксиоматической теории множеств противоположность платонистской и конструктивистской позиций практически невидима. Если математика, как полагает платонист, мыслится как открытие уже существующего универсума множеств, тогда аксиомы прямо утверждают существование множества, удовлетворяющего определенным условиям. Если же математика, как полагает концептуалист, является человеческим изобретением, тогда аксиомы утверждают способ порождения из одних заданных множеств других множеств. Математика в этом смысле представляет собой структуру, в которой непротиворечиво демонстрируется существование множества. Другими словами, аксиомы позволяют так ограничить понятие множества, чтобы избежать парадоксов независимо от взгляда на природу математики.
Похожие работы
... проверить знания студента из первой части курса, которая излагается в первых четырёх модулях. Во вторых вопросах билета проверяются знания классической предельной проблемы теории вероятностей и математической статистики, которые излагаются в следующих пяти модулях. 1. Вероятностная модель с не более чем счётным числом элементарных исходов. Пример: испытания с равновозможными исходами. 2. ...
... , почему именно эти аксиомы оказались настолько успешными и достойными специального внимания. Соответственно самая большая слабость формализма состоит в невозможности объяснить, почему аксиомы теории множеств, предположительно не отражающие никакой реальности, способны доказывать арифметические утверждения, не доказуемые с помощью более финитистских средств. Слабость, которую, как я полагаю, ...
... вующий класс (предложение 4), то из аксиомы S следует, что для любого множества х класс всех его элементов, удовлетворяющих данной предикативной формуле A(у), есть множество. Однако для полного развития теории множеств потребуется аксиома, более сильная, чем аксиома S. Введем предварительно несколько определений. Определения Un (X) означает xyz ( X & X y = z). (X однозначен.) ...
... монету второй раз не бросают), в четвертом — второму. Шансы игроков на выигрыш относятся как 3 к 1. В этом отношении и надо разделить ставку. Глава II. Элементы теории вероятностей и статистики на уроках математики в начальной школе (методика работы) Первый шаг на пути ознакомления младших школьников с миром вероятности состоит в длительном экспериментировании. Эксперимент повторяют много раз при ...
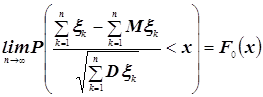
0 комментариев