Навигация
1.3. Равенство множеств
Определение равенства множеств. Множества А и B равны, если они состоят из одних и тех же элементов, то есть, если из xA следует xB и обратно, из xB следует xA.
Формально равенство двух множеств записывается следующим образом:
А=В ó x | xA ó xB.
Равенство множеств А и В записывают в виде А=В.
Чтобы доказать равенство двух множеств, необходимо доказать, что:
x | xA Þ xB;
x | x B Þ x A.
Пример.
Равенство всех пустых множеств (A=, B= Þ A=B).
А – множество корней уравнения (x-1)(x-2)=0. B – множество, состоящее из элементов 1 и 2: B={1,2}. A=B.
Глава 2. Основные теоретико-множественные отношения2.1. Подмножества
Определение подмножества. Множество А является подмножеством множества В, если любой элемент, принадлежащий множеству А, принадлежит множеству В.
Формальная запись: A B ó x | xA xB.
Если A является подмножеством B, то B называется надмножеством A.
Если среди данных множеств одно из них является подмножеством другого, это обозначает, что они связаны отношением включения.
Отношение нестрогого включения обозначается “”.
Отношение строгого включения обозначается “”.
AB обозначает, что множество A содержится в B, при чем А может быть равным множеству B. Строгое включение исключает такое равенство.
Если AB, A , то A – собственное подмножество множества В.
Свойства отношения включения.
A выполняется AA (рефлексивность).
A, B выполняется AB BA Þ A=B (антисимметричность).
A, B, C выполняется AB BC Þ AC (транзитивность).
Пример.
Пустое множество является подмножеством любого множества.
Множество {2, 4, 6, ... , 2n, ...} является собственным подмножеством множества натуральных чисел {1, 2, 3, 4…}.
2.2. Операции над множествами и их свойства
Основными операциями над множествами являются объединение, пересечение и разность.
Определение объединения множеств. Суммой, или объединением произвольного конечного или бесконечного множества множеств называется множество, состоящее из тех и только тех элементов, которые принадлежат хотя бы одному из множеств А, В. AB={x | xA V xB}.
Пример.
A={1, 3, 5}, B={2, 4, 6}. AB={1, 2, 3, 4, 5, 6}.
Определение пересечения множеств. Произведением, или пересечением любого конечного или бесконечного множества множеств называется множество, состоящее из тех и только тех элементов, которые принадлежат множествам А и В одновременно. AB = {x | xA xB}.
Если множества заданы характеристическими свойствами своих элементов, то из определения пересечения следует, что характеристическое свойство множества АВ составляется из характеристических свойств пересекаемых множеств с помощью союза “и”.
Пример.
A={1, 3, 5}, B={1, 3, 7, 9}. AB={1, 3}.
Определение разности множеств. Разностью между множеством A и множеством B называется множество всех элементов из A, не являющихся элементами множества B. AB = {x | xA xB}.
Если множества А и В заданы характеристическими свойствами их элементов, то из определения объединения следует, что характеристическое свойство элементов множества А U В составляется из характеристических свойств элементов множеств А и В с помощью союза “или”.
Пример.
A={1, 3, 5, 18}, B={1, 3, 7, 9}. AB={5, 18}.
Определение симметрической разности множеств. Симметрической разностью множеств A и B называется множество всех элементов из A, не являющихся элементами множества B в объединении с множеством всех элементов из B, не являющихся элементами множества A. A∆B=(AB)(BA).
Пример.
A={1, 3, 5, 18}, B={1, 3, 7, 12}. A∆B={5, 7, 12, 18}.
Определение абсолютного дополнения. Пусть A – подмножество U. Абсолютным дополнением множества A до множества U называется множество, содержащее все элементы множества U, которые не принадлежат множеству A. A'=![]() =UA, где U - универсальное множество.
=UA, где U - универсальное множество. ![]() =UA={x | xU xA}.
=UA={x | xU xA}.
Обычно все рассматриваемые в ходе какого-либо рассуждения множества являются подмножествами некоторого множества U, которое называют универсальным. Например, для числовых множеств универсальным является R, для точечных множеств на плоскости - множество точек всей плоскости и т.д.
Приоритеты операций.
Под приоритетом операции понимается порядок ее выполнения. Первой выполняется та операция, приоритет которой выше.
Приоритет операции пересечения множеств выше приоритета операции объединения.
Приоритет операции пересечения множеств выше приоритета операции вычитания.
Объединение и вычитание множеств считают равноправными операциями.
Пример. В выражении CАВ надо сначала выполнить вычитание (из А вычесть В), а затем полученное множество объединить с множеством С.
Свойства операций над множествами.
1. A, AA=A. AA=A (идемпотентность).
2. Пересечение и объединение множеств коммутативно (перестановочно):
A ,B AB = BA; A ,B AB = BA.
Доказательство.
Эти свойства вытекают из определения. Действительно, пусть xAB, тогда xA и xB, следовательно, xBA. Отсюда (AB)(BA). Аналогично доказывается обратное утверждение (BA)(AB). Отсюда AB = BA.
Пусть xAB, тогда либо xA, либо xB, но тогда xBA и (AB) (BA). Аналогично (BA) (AB). Следовательно, AB = BA.
3. Пересечение и объединение множеств ассоциативно: для любых множеств A, B и C имеем (AB)C=A(BC); (AB)C=A(BC).
Доказательство.
Пусть x(AB)C, отсюда x(AB) и xC, или xA, xB, xC. Отсюда x(BC) и xA, следовательно, xA(BC) и верно (AB)CA(BC). Наоборот, если xA(BC), следует, что xA, xC, xB, откуда x(AB)C и верно A(BC)(AB)C. Отсюда A(BC) = (AB)C. Аналогично доказывается равенство множеств A(BC) = (AB)C.
Похожие работы
... проверить знания студента из первой части курса, которая излагается в первых четырёх модулях. Во вторых вопросах билета проверяются знания классической предельной проблемы теории вероятностей и математической статистики, которые излагаются в следующих пяти модулях. 1. Вероятностная модель с не более чем счётным числом элементарных исходов. Пример: испытания с равновозможными исходами. 2. ...
... , почему именно эти аксиомы оказались настолько успешными и достойными специального внимания. Соответственно самая большая слабость формализма состоит в невозможности объяснить, почему аксиомы теории множеств, предположительно не отражающие никакой реальности, способны доказывать арифметические утверждения, не доказуемые с помощью более финитистских средств. Слабость, которую, как я полагаю, ...
... вующий класс (предложение 4), то из аксиомы S следует, что для любого множества х класс всех его элементов, удовлетворяющих данной предикативной формуле A(у), есть множество. Однако для полного развития теории множеств потребуется аксиома, более сильная, чем аксиома S. Введем предварительно несколько определений. Определения Un (X) означает xyz ( X & X y = z). (X однозначен.) ...
... монету второй раз не бросают), в четвертом — второму. Шансы игроков на выигрыш относятся как 3 к 1. В этом отношении и надо разделить ставку. Глава II. Элементы теории вероятностей и статистики на уроках математики в начальной школе (методика работы) Первый шаг на пути ознакомления младших школьников с миром вероятности состоит в длительном экспериментировании. Эксперимент повторяют много раз при ...
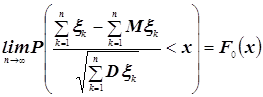
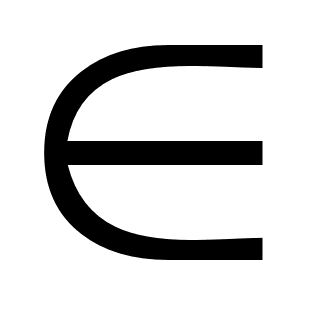
0 комментариев