Навигация
Изменение коэффициента целевой функции базисной переменной приводит к изменению значения целевой функции
2. Изменение коэффициента целевой функции базисной переменной приводит к изменению значения целевой функции.
3. Эффект от изменения коэффициентов целевой функции можно рассматривать с двух позиций: с точки зрения сбыта нас интересуют равновесные цены; с точки зрения производства нас интересует диапазон изменения коэффициентов целевой функции, в пределах которого текущий план ( представленный текущим базисом ) остается оптимальным.
Изменение компонент вектора ограниченийРассмотрим влияние изменения Bi = Bi + q для некоторого 1 <= i <= m Обычно принято рассматривать случай, когда компонента Bi является правой частью ограничения-неравенства в которое введена дополнительная переменная. Мы хотим определить такой диапазон изменения Bi в котором текущее решение остается оптимальным. В случае ограничения-равенства мы могли бы рассматривать соответствующую искусственную переменную как неотрицательную дополнительную (которая должна быть небазисной в допустимом решении)
а) Базисная дополнительная переменная
Если дополнительная переменная i-го ограничения базисная то это ограничение не является активным в точке оптимума. Анализ прост: значение дополнительной базисой переменной дает диапазон изменения, в котором соответствующая компонента Bi уменьшается (увеличивается в случае ограничения типа =>).
Решение остается допустимым и оптимальным в диапазоне Bi + q, где
-Xs <= q <= +oo для ограничений типа <=
-oo <= q <= Xs для ограничений типа =>
Здесь Xs - значение соответствующей дополнительной переменной. Например рассмотрим ограничение-неравенство:
3X1 + 4X2 + 7X3 <= 100
Приведем его к равенству введя дополнительную переменную
3X1 + 4X2 + 7X3 + X4 = 100
Если в оптимальном решении X4 = 26 то оставшиеся переменные удовлетворяют неравенству:
3X1 + 4X2 + 7X3 <= 74
а также любому неравенству того же вида со значением правой части большим 74.
б) Небазисная дополнительная переменная
Если дополнительная переменная небахзисная и равна нулю, то исходное ограничение-неравенство является активным в точке оптимума. На первый взгляд может показаться что так как это ограничение активное то отсутствует возможность изменения значения правой части такого ограничения, в частности возможность уменьшения значения Bi (для ограничений типа <=). Оказывается что изменяя вектор В мы меняем также вектор Xb и так как существует диапазон изменений в котором Xb неотрицателен, то решение остается еще и оптимальным в том смысле, что базис не меняется. (Заметим что при этом изменяется значение как Xb так и Р).
Рассмотрим ограничение:Ak1X1+Ak2X2 +. . . +Xs = Bk где Xs - дополнительная переменная. Пусть теперь правая часть станет равной Bk + q, тогда уравнение можно переписать так: 1. 1) Ak1X1+Ak2X2 +. . . +(Xs-q) = Bk
Так что (Xs - q) заменяет Xs Следовательно, если в оптимальном решении переменная Xs небазисная и равна нулю то мы имеем Xb = B - As*(-q) где As - столбец конечной таблицы соответствующий Xs. Так как Xs должен оставаться неотрицательным то мы получаем соотношение: B - As*(-q) => 0 которое определяет диапазон изменения q:
MAX {Bi/-Ais} <= q <= MIN {Bi/-Ais}
i/Ais>0 i/Ais<0
Если нет ни одного Ais > 0 то q > -oo,
а если нет ни одного Ais < 0 то q < +oo
Для ограничений типа => q меняет знак, так как вместо неравенства E AijXj => Bi мы можем рассматривать
-E AijXj <= -Bi
Поэтому в уравнении 1. 1) вместо +(Xs-q) мы должны писать -(Xs+q).
Снова рассмотрим пример:
Максимизировать Р= 31. 5 -3. 5X4 -0. 1X3 -0. 25X
При условиях X1 = 3. 2 -1. 0X4 -0. 5X3 -0. 60X5
X2 = 1. 5 +0. 5X4 +1. 0X3 -1. 00X5
X6 = 5. 6 -2. 0X4 -0. 5X3 -1. 00X5
Пусть X4 - дополнительная переменная некоторого ограничения i (типа <=). Если компонену Bi изменить на величину q, мы получим:
X1 = 3. 2 - 1. 0*(-q)
X2 = 1. 5 + 0. 5*(-q)
X6 = 5. 6 - 2. 0*(-q)
3. 2 1. 0
то есть B = 1. 5 As = -0. 5
5. 6 2. 0
Тогда,
X1 => 0 при 3. 2 - 1. 0*(-q) => 0, то есть q => 3. 2/-1. 0,
X2 => 0 при 1. 5 + 0. 5*(-q) => 0, то еасть q <= 1. 5/0. 5,
X6 => 0 при 5. 6 - 2. 0*(-q) => 0, то есть q => 5. 6/-2. 0
Значит q может меняться в диапазоне:
MAX {3. 2/-1. 0; 5. 6/-2. 0} <= q <= 1. 5/0. 5, то есть -2. 8 <= q <= 3. 0
ВЫРОЖДЕННОСТЬ1. Вырожденность прямой задачи
Вырожденное решение прямой задачи характеризуется тем, что его базисная компонента равна нулю. Вырожденность прямой задачи может часто проявляться через промежуточные (неоптимальные) вырожденые базисные решения. Так например не произойдет улучшения целевой функции от введения в базис переменной, для которой положительна соответствующая компонента вектор а Aq.
Возможен случай, когда прямая задача ЛП имеет вырожденое промежуточное но невырожденное оптимальое решение. Если оптимально решение прямой задачи вырождено, то двойственная задача имеет бесконечно много оптимальных решеий.
Похожие работы
... ; b x, y ≥ 0. b принимает значение 18 с вероятностью и значение 45 с вероятностью . Экзаменационный билет по предмету МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ЭКОНОМИКИ Билет № 1 1) Показать результат произведения матрицы размерности m х n на вектор- ...
... + 6y ≤ b x, y ≥ 0. b принимает значение 18 с вероятностью и значение 45 с вероятностью . Экзаменационный билет по предмету МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ЭКОНОМИКИ Билет № 1 1) Дать определение умножения матрицы на число. 2) Записать общую задачу ...
... Найти произведение матриц А = и В = Вычислить значение функции f (x1, x2, x3, x4) = 8 x1 x2 + 4 + 10 x1 (x4)2 в точке (1, 2, 4, 3) Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ЭКОНОМИКИ Билет № 16 Объяснить связь базиса и размерности пространства. Дать основные положения задачи ...
... системы цен по остальным товарам. Конец XIX – начало XX века ознаменовались широким использованием математики в экономике. В XX в. математические методы моделирования используются столь широко, что почти все работы, удостоенные Нобелевской премии по экономике, связаны с их применением (Д. Хикс, Р. Солоу, В. Леонтьев, П. Самуэльсон, Л. Канторович и др.). Развитие предметных дисциплин в большинстве ...
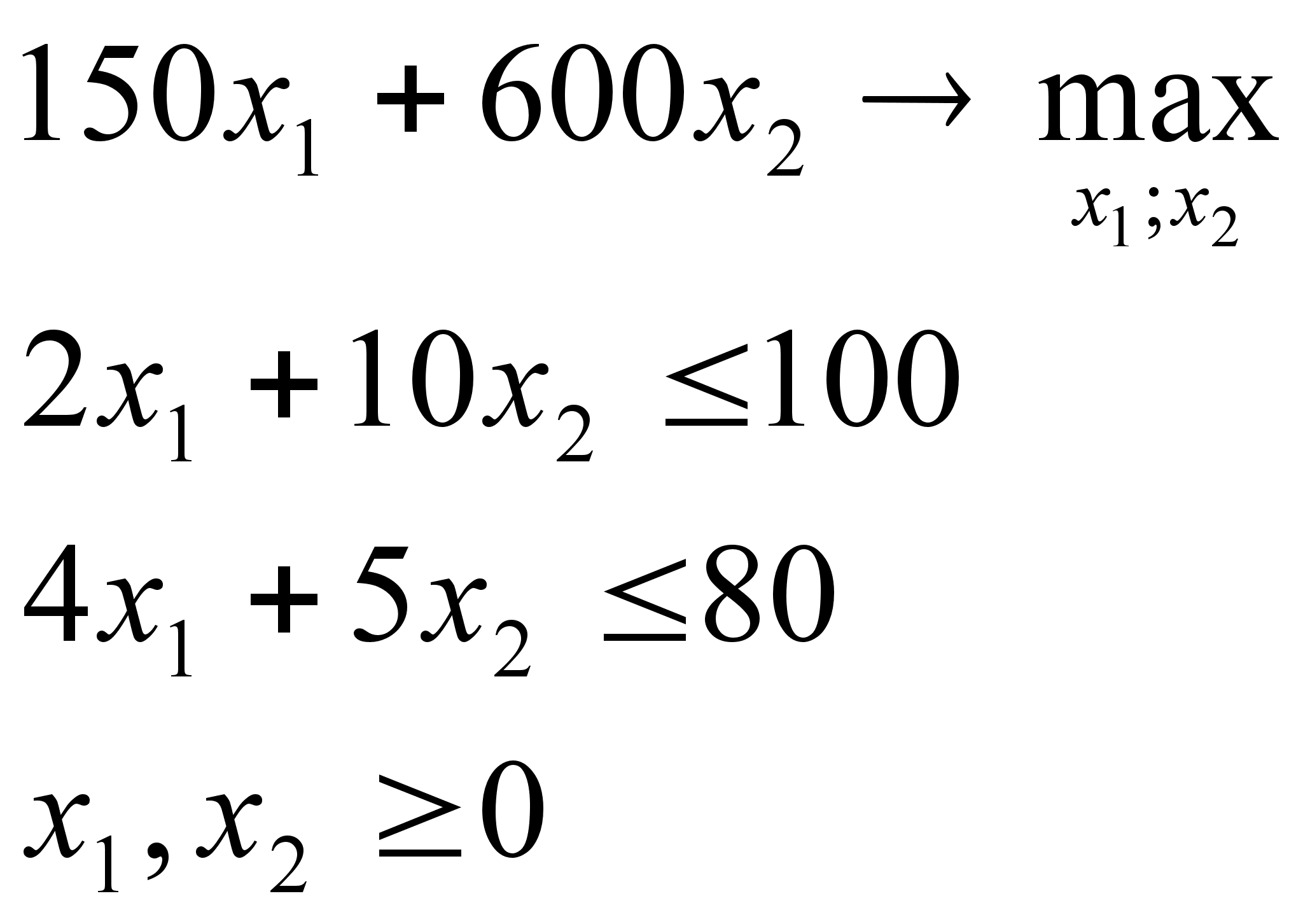
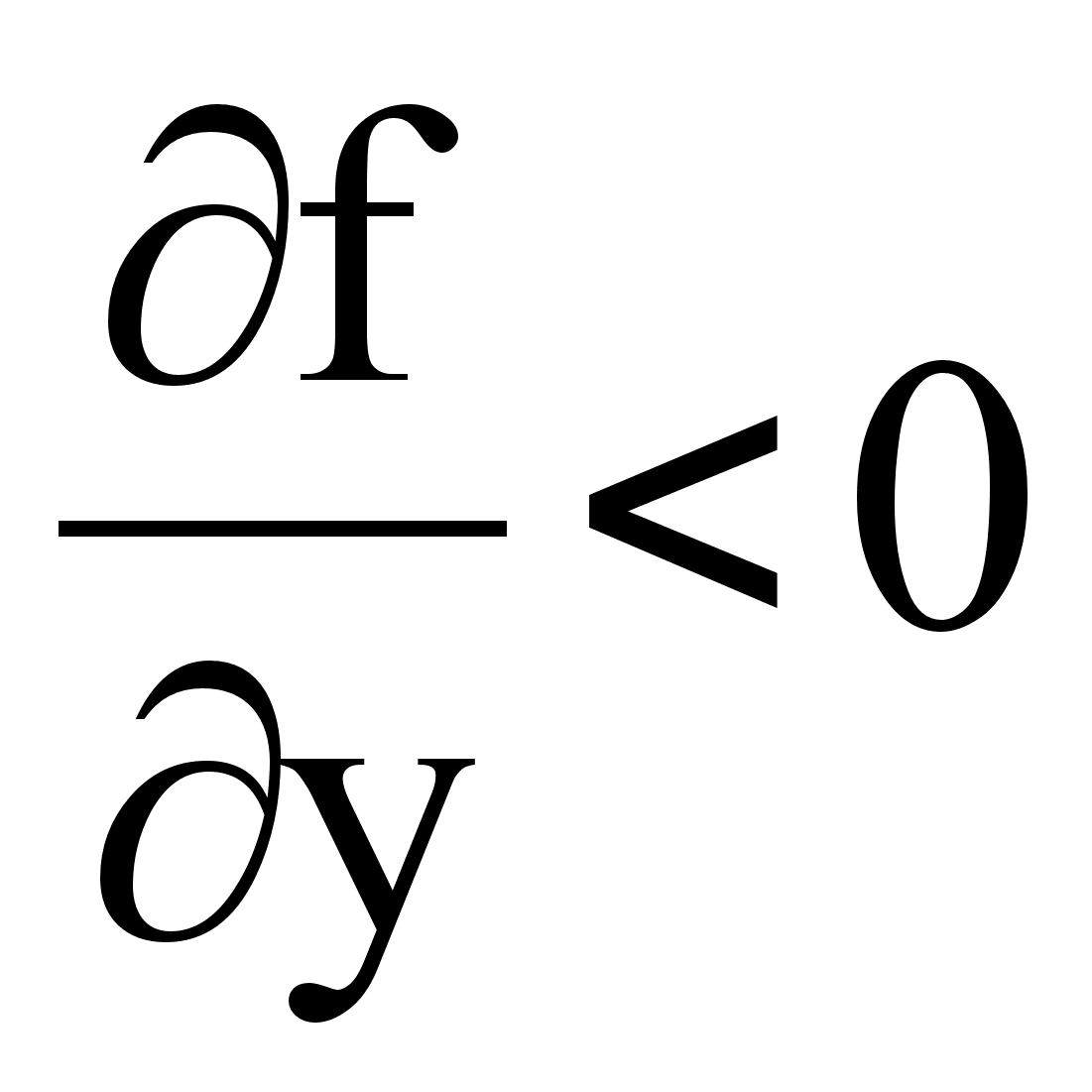
0 комментариев