Навигация
4.2.2 Кванторы.
В алгебре предикатов наряду с операциями логики высказываний важнейшую роль играют операции, называемые кванторами. Именно употребление кванторов делает алгебру предикатов значительно более богатой, чем алгебру высказываний. Кванторы соответствуют по смыслу тому, что на обычном языке выражается словами «все» («для каждого», «для всех» и т. п.) и «существует» («некоторый», «найдется» и т. п.).
Понятие, обозначаемое словом «все», лежит в основе квантора всеобщности (или квантора общности). Если через Гр (X) обозначен предикат «X есть грек», определенный на множестве М всех людей, то из этого предиката с помощью слова «все» мы можем построить высказывание «Все люди – греки» (конечно, ложное высказывание). Это пример применения квантора всеобщности.
Вообще же квантор всеобщности определяется так. Пусть Р (X) – какой-нибудь предикат. Тогда квантор всеобщности – это операция, которая сопоставляет Р (X) высказывание
«Все X обладают свойством Р (X)». (*)
Для этой операции («все») употребляется знак ![]() (перевернутая латинская буква А, напоминающая о немецком слове «alle» или английском «all» – все). Высказывание (*) записывается так:
(перевернутая латинская буква А, напоминающая о немецком слове «alle» или английском «all» – все). Высказывание (*) записывается так: ![]() (X)P(X) (читается: «для всех X Р от X»). В соответствии со смыслом слова «все»
(X)P(X) (читается: «для всех X Р от X»). В соответствии со смыслом слова «все» ![]() (X)Р(X) – ложное высказывание, кроме того единственного случая, когда Р (X) тождественно-истинный предикат.
(X)Р(X) – ложное высказывание, кроме того единственного случая, когда Р (X) тождественно-истинный предикат.
Наряду с квантором всеобщности в логике предикатов рассматривается другой квантор – «двойственный» ему квантор существования, обозначаемый знаком ![]() (это перевернутая латинская буква E, напоминающая немецкое слово «existieren» или английское «exist» — существовать):
(это перевернутая латинская буква E, напоминающая немецкое слово «existieren» или английское «exist» — существовать):
![]() (Х)Р(Х)
(Х)Р(Х)
(читается: «существует такое X, что Р от X») – высказывание, которое истинно тогда и только тогда, когда Р истинно по меньшей мере для одного объекта а из области определения М. Тем самым ![]() (X)Р(X) – истинное высказывание для всех предикатов Р (X), кроме одного – тождественно-ложного.
(X)Р(X) – истинное высказывание для всех предикатов Р (X), кроме одного – тождественно-ложного.
Между кванторами ![]() и
и ![]() имеют место отношения равносильности, позволяющие сводить любой из этих кванторов к другому: ù
имеют место отношения равносильности, позволяющие сводить любой из этих кванторов к другому: ù ![]() (X) P(X) Û
(X) P(X) Û![]() (X) ù P(X) («Неверно, что все X обладают свойством Р (X)» равносильно тому, что «Существует такой объект X, для которого истинно не Р (X)»). Отсюда имеем:
(X) ù P(X) («Неверно, что все X обладают свойством Р (X)» равносильно тому, что «Существует такой объект X, для которого истинно не Р (X)»). Отсюда имеем: ![]() (X) Û ù
(X) Û ù![]() (X)ù P(X). Аналогично, имеет место двойственный закон: ù
(X)ù P(X). Аналогично, имеет место двойственный закон: ù![]() (X) P(X) Û
(X) P(X) Û ![]() (X)ù P(X). («Неверно, что существует X, обладающее свойством Р (X)» равносильно «Все X обладают свойством не Р (X)»).
(X)ù P(X). («Неверно, что существует X, обладающее свойством Р (X)» равносильно «Все X обладают свойством не Р (X)»).
Отсюда ![]() (X)Р(X)Ûù
(X)Р(X)Ûù![]() (X)ùP(X). Эти равносильности называют правилами де Моргана для кванторов.
(X)ùP(X). Эти равносильности называют правилами де Моргана для кванторов.
С помощью квантора существования легко выражается суждение типа «Некоторые Р суть Q» (например, «Некоторые англичане курят», «Некоторые нечетные числа – простые» и т. п.), т. е. что по крайней мере один объект а, обладающий свойством Р, обладает также свойством Q. Этот факт записывается формулой ![]() (X)(Р(X)ÙQ(X)) («Существует такой X, что Р от X и Q от X»).
(X)(Р(X)ÙQ(X)) («Существует такой X, что Р от X и Q от X»).
Аналогично с помощью кванторов записывается ряд других отношений между одноместными предикатами.
Гораздо более богатые возможности открывает применение кванторов к многоместным предикатам. Остановимся вкратце на этом вопросе.
Пусть А (X, Y) – некоторый двухместный предикат, определенный на некотором множестве М. Квантор всеобщности и квантор существования можно применять к нему как для переменной X, так и для переменной Y: ![]() (X)А(X, У);
(X)А(X, У); ![]() (Y)А(X, Y);
(Y)А(X, Y); ![]() (X)А(Х,Y);
(X)А(Х,Y); ![]() (Y)A(X,Y). Переменная, к которой применен квантор, называется связанной, другая переменная – свободной. Все четыре приведенных выражения являются записями одноместных предикатов от соответствующей свободной переменной.
(Y)A(X,Y). Переменная, к которой применен квантор, называется связанной, другая переменная – свободной. Все четыре приведенных выражения являются записями одноместных предикатов от соответствующей свободной переменной. ![]() (X)А(X,Y) (читается: «для всех X, A от X и Y») – одноместный предикат от переменной Y:
(X)А(X,Y) (читается: «для всех X, A от X и Y») – одноместный предикат от переменной Y: ![]() (X)А (X,Y)=F(У), Он истинен в точности для тех bÎМ, для которых одноместный предикат А (X, b) истинен для всех X. Если представить предикат А (X, Y) его таблицей, то предикат F (Y) =
(X)А (X,Y)=F(У), Он истинен в точности для тех bÎМ, для которых одноместный предикат А (X, b) истинен для всех X. Если представить предикат А (X, Y) его таблицей, то предикат F (Y) = ![]() (X) (X, Y) истинен для тех b, для которых столбец с входом b содержит исключительно букву и.
(X) (X, Y) истинен для тех b, для которых столбец с входом b содержит исключительно букву и.
Применение квантора к одной из переменных двухместного предиката превращает его в одноместный. В случае трехместных предикатов применение квантора приводит к двухместному предикату. Аналогично и для предикатов с большим числом мест применение квантора превращает n-местный предикат в (n – 1)-местный.
К свободной переменной X одноместного предиката ![]() (У)А(X, Y) в свою очередь можно применять квантор всеобщности или квантор существования. Получаются выражения
(У)А(X, Y) в свою очередь можно применять квантор всеобщности или квантор существования. Получаются выражения
![]() (X)(
(X)(![]() (У)А(X,У));
(У)А(X,У)); ![]() (X)(
(X)(![]() (Y)А(X,У)), которые, опуская скобки, принято записывать несколько проще:
(Y)А(X,У)), которые, опуская скобки, принято записывать несколько проще: ![]() (X)
(X)![]() (У)А(X,У);
(У)А(X,У); ![]() (X)
(X)![]() (Y)А(X,У),
(Y)А(X,У),
Это – высказывания. Первое истинно, если все строки, а тем самым и вся таблица предикатов, содержат только букву и, второе истинно, если соответствующая матрица содержит по меньшей мере одну тождественно-истинную строку. Три другие предиката ![]() (X)А (X,У),
(X)А (X,У), ![]() (У)А(X, У) и
(У)А(X, У) и ![]() (X)А (X,У) также допускают квантификацию, так что в общей сложности мы получаем из одного предиката восемь формально различных высказываний:
(X)А (X,У) также допускают квантификацию, так что в общей сложности мы получаем из одного предиката восемь формально различных высказываний: ![]() (X)
(X)![]() (У)А (X, У);
(У)А (X, У); ![]() (X)
(X)![]() (У)А (X,У);
(У)А (X,У); ![]() (X)
(X)![]() (У)А (X, У);
(У)А (X, У); ![]() (X)
(X)![]() (У)А (X, У);
(У)А (X, У); ![]() (У)
(У)![]() (X) А (X, У);
(X) А (X, У); ![]() (У)
(У)![]() (X)А(X, У);
(X)А(X, У); ![]() (У)
(У)![]() (X)А (X, У);
(X)А (X, У); ![]() (Y)
(Y)![]() (X) А (X, У).
(X) А (X, У).
Нетрудно убедиться в том, что четыре высказывания, содержащие одинаковые кванторы, попарно эквивалентны:
![]() (X)
(X)![]() (У)А(X,У) Û
(У)А(X,У) Û![]() (У)
(У)![]() (X)А (X, У);
(X)А (X, У);
![]() (X)
(X)![]() (У)А (X, У) Û
(У)А (X, У) Û ![]() (Y)
(Y)![]() (X)А (X, У).
(X)А (X, У).
![]() (X)
(X)![]() (У)А(X,У) так же как и
(У)А(X,У) так же как и ![]() (У)
(У)![]() (X)А(X, У), истинно тогда и только тогда, когда А (X, У) – тождественно-истинный предикат,
(X)А(X, У), истинно тогда и только тогда, когда А (X, У) – тождественно-истинный предикат, ![]() (X)
(X)![]() (У)А (X, У) и
(У)А (X, У) и ![]() (Y)
(Y)![]() (X)А(X,У) оба истинны во всех случаях, кроме одного, когда А(X,У) – тождественно-ложный предикат. Все остальные высказывания существенно различны. Особенно следует помнить, что порядок следования разноименных кванторов очень важен.
(X)А(X,У) оба истинны во всех случаях, кроме одного, когда А(X,У) – тождественно-ложный предикат. Все остальные высказывания существенно различны. Особенно следует помнить, что порядок следования разноименных кванторов очень важен.
Я считаю, что к окончанию школы ученики должны овладеть кванторами, но введение их должно быть постепенным и начинаться в простых ситуациях. Учащиеся должны хорошо понимать, что от перестановки кванторов может меняться смысл утверждения.
Например, Пусть I=(а,b) – некоторый интервал. Тогда «Для всякого хÎI существует такой у, что у = f (х)» (![]() (x)
(x)![]() (у) (у = f (х))), означает, что функция f(х) всюду определена на I. Напротив, «Существует такое у, что для всякого х у=f (х)» (
(у) (у = f (х))), означает, что функция f(х) всюду определена на I. Напротив, «Существует такое у, что для всякого х у=f (х)» (![]() (у)
(у)![]() (х)(у=f(х))) означает, что функция f(x) принимает для всех х некоторое фиксированное значение у, т. е. постоянна.
(х)(у=f(х))) означает, что функция f(x) принимает для всех х некоторое фиксированное значение у, т. е. постоянна.
Приведем еще один пример. Корректное определение периодичности всюду определенной функции f(х) выглядит с использованием кванторов так: ![]() (c)
(c)![]() (x) (c¹0 Ù Ùf(x+c) = f(x)), между тем если переставить кванторы и сформулировать утверждение «Для каждого х существует такое с, что с¹0 и что f(х + с) =f(x)»:
(x) (c¹0 Ù Ùf(x+c) = f(x)), между тем если переставить кванторы и сформулировать утверждение «Для каждого х существует такое с, что с¹0 и что f(х + с) =f(x)»: ![]() (c)
(c)![]() (x) (c¹0 Ù f(x+c) = f(x)), то это означает лишь, что функция принимает каждое значение больше чем один раз, т. е. нечто совсем иное.
(x) (c¹0 Ù f(x+c) = f(x)), то это означает лишь, что функция принимает каждое значение больше чем один раз, т. е. нечто совсем иное.
В математическом анализе часто приходится сталкиваться с кванторами.
Определение предела последовательности из учебника «Алгебра и начала анализа» для 10-11 классов сформулировано так «Число А является пределом последовательности аn, если для любого ![]() >0 существует номер N, такой, что при всех n>N верно неравенство
>0 существует номер N, такой, что при всех n>N верно неравенство ![]() ». В кванторном обозначении это определение записывается так:
». В кванторном обозначении это определение записывается так:
![]() (
(![]() >0)
>0)![]() (NÎN)
(NÎN)![]() (n ÎN)((n>N) Þ
(n ÎN)((n>N) Þ ![]()
Переставлять кванторы нельзя: именно тот факт, что N под квантором существования ![]() следует за выражением
следует за выражением ![]() (
(![]() > 0), указывает на зависимость N от выбранного
> 0), указывает на зависимость N от выбранного ![]() .
.
Как выразить утверждение, что последовательность (хn) сходится? Надо указать на то, что предел A существует. С помощью кванторов это утверждение формулируется так:
![]() (A)
(A) ![]() (
(![]() > 0)
> 0) ![]() (NÎ N)
(NÎ N) ![]() (nÎN)((n > N) Þ (
(nÎN)((n > N) Þ (![]() )).
)).
Такая запись имеет еще и то преимущество, что она почти автоматически позволяет формулировать отрицание существования предела, означающее свойство расходимости. Для этого достаточно несколько раз применить правило де Моргана для кванторов: (хn) расходится Ûù(![]() (A)
(A) ![]() (
(![]() > 0)
> 0) ![]() (NÎ N)
(NÎ N) ![]() (nÎN)((n > N) Þ (
(nÎN)((n > N) Þ (![]() )) Û
)) Û ![]() (A)
(A)![]() (
(![]() > 0)
> 0) ![]() (NÎ N)
(NÎ N) ![]() (nÎN)((n > N) Ù
(nÎN)((n > N) Ù![]() ).
).
Задания для учащихся.
Установите, какие из следующих высказываний истинны.
![]() x (x + 1 = x);
x (x + 1 = x); ![]() x (x2 + x + 1>0);
x (x2 + x + 1>0); ![]() x (x2 - 5x + 6>0);
x (x2 - 5x + 6>0); ![]() x (x2 -6x+8³0 Ù x2-4x+3>0);
x (x2 -6x+8³0 Ù x2-4x+3>0); ![]() x (x2 - 5x + 6 ³ 0 Ú x2 + 5x + 6 < 0)
x (x2 - 5x + 6 ³ 0 Ú x2 + 5x + 6 < 0)
2) При каких аÎR истинны следующие высказывания: ![]() х (x2 +x + а>0);
х (x2 +x + а>0);
![]() x (x2 +x + а>0);
x (x2 +x + а>0); ![]() х (x2 +ax + 1>0);
х (x2 +ax + 1>0);
3) Пусть P(x) = «х – простое число»
E(x) = «х – четное число»
Z(x) = «х – целое число»
D(x,y) = «y делится на х»
G(x,y) = «х > y»
Расшифруйте следующие высказывания и выясните, какие из них истинны:
P(x)ÞùE(x); ![]() x (E(x) Ú D(x,6));
x (E(x) Ú D(x,6));
![]() x(P(x)ÞùE(x);
x(P(x)ÞùE(x); ![]() x(P(x)ÚE(x));
x(P(x)ÚE(x));
![]() x
x![]() y(D(x,y)ÞG(y,x));
y(D(x,y)ÞG(y,x)); ![]() x
x![]() y(Z(x)ÙZ(y)ÞD(x,y));
y(Z(x)ÙZ(y)ÞD(x,y));
![]() x
x![]() y(Z(x)ÙZ(y)ÞD(x,y)).
y(Z(x)ÙZ(y)ÞD(x,y)).
4) Запишите с помощью кванторов определение предела функции: число b называется пределом функции f(х) при х, стремящемся к а, если для любого положительного числа ![]() найдется такое положительное число
найдется такое положительное число ![]() , что при всех х ¹ а, удовлетворяющих неравенству ½х – а½<0, будет выполнено неравенство ½f (х) – b½<
, что при всех х ¹ а, удовлетворяющих неравенству ½х – а½<0, будет выполнено неравенство ½f (х) – b½< ![]() .
.
§5 Методические рекомендации к теме «Введение нуля и развитие позиционной десятичной системы счисления».
В 5 классе уже возможно обсуждение с учащимися этой темы.
Можно вспомнить с ними, что счет у нас ведется десятками: десять единиц образуют один десяток, десять десятков – одну сотню и т.д., иными словами: десять единиц первого разряда образуют одну единицу второго разряда, десять единиц второго разряда – одну единицу третьего разряда и т.д.
Такой способ счета, группами в десять, которым мы пользуемся, называется десятичной системой счисления. Число десять называется основанием десятичной системы счисления. Строго определения десятичной системы давать не стоит.
Затем, нужно обсудить, почему мы считаем именно десятками, то есть как возникла десятичная система счисления?
Люди на первых ступенях развития общества считали с помощью десяти пальцев рук. Сейчас иногда говорят: «Перечесть по пальцам».
Далее следует поговорить о том, что были племена и народы, которые при счете пользовались лишь пятью пальцами одной руки, считали пятками, поэтому и использовали они пятеричную систему счисления, в которой основой служит число 5.
Существуют и другие системы счисления: двоичная, двадцатеричная (следы ее сохранились до сих пор во французском языке – они говорят вместо «восьмидесяти» - «четырежды двадцать»). Двадцатеричная система возникла у народов, считавших не только с помощью пальцев рук, но и пальцев ног. Древние вавилоняне пользовались шестидесятеричной системой счисления.
Можно обсудить, сколько цифр используется в каждой из перечисленных систем счисления для изображения чисел.
Также полезно для учащихся будет ознакомиться с римской нумерацией, обсудить где она применяется. Учащиеся должны научиться записывать арабские числа с помощью римских. Тут же можно предложить им пару занимательных задач, где используют римские цифры с целью привлечения их внимания.
Больше никакие алфавитные системы не стоит затрагивать, а только продемонстрировать табличку с алфавитными нумерациями, а также числовые знаки различных народов (см. дальше).
После этого учащимся можно сообщить вкратце о происхождении знака 0.
Нужно отметить, что сейчас нуль это не просто знак для отделения разрядов, а число, которое можно складывать, вычитать, умножать и делить, как и другие числа. Единственное ограничение – делить на 0 нельзя.
Возможно вынесение этого материала на факультативные занятие, где обсуждению различных систем счисления можно отвести больше времени.
С учащимися 7-8 классов возможно более полное рассмотрение этой темы.
Начать следует с рассказа о том, что существуют позиционные и непозиционные системы счисления. Дать определения одной и другой системы счисления, попросить учащихся привести примеры.
Затем можно обсудить двоичную систему. Учащиеся должны научиться переводить числа из двоичной системы счисления в десятичную, и наоборот. После этого подобные действия проделать с другой системой счисления, например, пятеричной. Можно научить учащихся складывать и умножать числа в различных системах счисления, отличных от десятичной. Далее, я считаю, что нужно рассмотреть десятичную непозиционную систему (например, древних египтян). Учащиеся должны понять, насколько тяжело изображать большие числа в непозиционных системах счисления. Только тогда они смогут по достоинству оценить заслугу индийских математиков, которые создали десятичную позиционную систему счисления.
Прежде чем начать рассказ о происхождение знака нуля можно предложить учащимся записать число сто три тысячи двести пятьдесят с помощью цифр, но не используя знака нуля. Обсудить как они это сделали, далее предложить сложить это число с числом двадцать тысяч семьсот восемьдесят девять, опять таки записанного с помощью цифр, но без знака нуля. У учащихся возникнут некоторые затруднения. После этого будет целесообразно рассказать им о заслуге индийцев.
Если кто-то из учащихся заинтересуется нумерациями различных народов, то можно предложить им для самостоятельного изучения книгу Э. Кольмана «История математики в древности».
Список литературы
Алексеев Б. Т. Философские проблемы формализации знания. Издательство ленинградского университета. 1981.
Бурбаки Н. Очерки по истории математики. М., издательство иностранной литературы. 1963.
Вилейтнер Г. История математики от Декарта до середины XIX столетия. М., «Наука». 1966.
Выгодский М.Я. Арифметика и алгебра в древнем мире. М., «Наука». 1967.
Глейзер Г.И. История математики в школе. Пособие для учителей. Под ред. В.Н. Молодшего. М., «Просвещение», 1964.
Калужнин Л.А. Элементы теории множеств и математической логики в школьном курсе математики. Пособие для учителей. М., «Просвещение», 1978. 88с.
Нешков К.И. И др. Множества. Отношения. Числа. Величины. Пособие для учителей. М. «Просвещение», 1978. 63 с.
Марков С.Н. Курс истории математики: Учебное пособие. – Иркутск: Издательство иркутского университета, 1995. – 248с.
Молодший В.Н. Очерки по истории математики. М.
Никифоровский В.А. Из истории алгебры XVI-XVII вв.. М., «Наука». 1979.
Петров Ю.А. Философские проблемы математики. М., «Знание», 1973.
Погребысский И.Б. Гольфрид Вильгельм Лейбниц. М., «Наука». 1971.
Рыбников К.А. История математики. Издательство московского университета. 1974.
Таваркиладзе Р.К. О языке школьного курса математики. «Математика в школе».
Хрестоматия по истории математики. Арифметика и алгебра. Теория чисел. Геометрия. Пособие для студентов физ.-мат. фак. пед. институтов. Под ред. А.П. Юшкевича. М., «Просвещение», 1976.
Энциклопедический словарь юного математика. М., «Педагогика». 1989.
Похожие работы
... neat as ninepence - чистенький, аккуратный; с иголочки; a twice-told tale - старая история, что-либо часто повторяемое и потому хорошо известное. 2. Значения числовых компонентов в английских фразеологических единицах Имена числительные, являясь абстрактным показателем количества однородных предметов, обозначением их счета, замкнуты в своеобразную категорию количественных слов, которые лишены ...
... схемы; 9) способность к пространственным представлениям, которая прямым образом связана с наличием такой отрасли математики, как геометрия, Сторонники шестого подхода считают, что математическое мышление является мышлением теоретическим и имеет такую же последовательность становления от эмпирического к аналитическому, к планирующему, рефлексирующему (Р. Атаханов, В.В. Давыдов, Ле Тхи Кхань Кхо, ...
... с активными познавательными обследовательскими действиями, со способностью к замещению предметов посредством условных знаков, символов».(7,с.126) 3. Моделирование в развитии математических представлений дошкольников Поиск эффективных средств познавательного развития детей, выявление условий становления познавательной деятельности в дошкольном детстве является темой научных работ многих ...
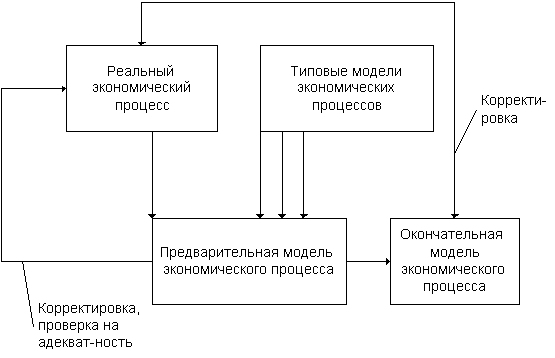
... заданное его качество, определение оптимальных (с точки зрения принятого критерия) норм дежурного обслуживания, надобность в котором возникает непланомерно, нерегулярно. С использованием метода математического моделирования можно определить, например, оптимальное количество автоматически действующих машин, которое может обслуживаться одним рабочим или бригадой рабочих и т.п. Типичным примером ...
0 комментариев